08届高考数学命题走势函数练习

08届高考数学命题走势函数练习（二）

函数是高考数学中极为重要的内容，函数的观点和方法既贯穿了高中代数的全过程，又是学习高等数学的基础.纵观近几年来的高考试题，函数在选择、填空、解答三种题型中每年都有试题，约含全卷的30%左右.近几年的考点主要体现在以下几个方面：

一、　　　　　　  纯粹函数内容（即单调性、奇偶性、定义域、值域、反函数）及映射概念的考查常以选择题、填空题出现，其能力要求比较低.

【例1】　（07年广东）已知函数的定义域为M，g(x)=的定义域为N，则M∩N=

  （A） （B）　（C）　 （D）

【解析】　M={xx<1},N={xx>-1},M∩N={x-1<x<1}.答案为C.

【说明】　考查了函数的定义域.

【例2】 （07年全国）设，函数在区间上的最大值与最小值之差为，则（  ）

A．　　　　 B．　　　　　　C．　　　　　　　D．

【解析】 .答案为D.

【说明】 对数函数的最值问题.

【例3】(07年安徽)下列函数中，反函数是其自身的函数为　　 （　　）

(A)　　　　　　　  （B）

(C)　　　　　　　 (D)

【解析】在下列函数中，反函数是其自身的函数为，选D.

【说明】　考查了反函数的求法.

【例4】 （07年安徽）定义在R上的函数既是奇函数，又是周期函数，是它的一个正周期.若将方程在闭区间上的根的个数记为，则可能为

　（A）0　　　　　　　　　　　　　　（B）1　　　　　　　　　　　　　　　 （C）3　　　　　　　　　　　　（D）5

【解析】，，

∴，则可能为5，选D。

【说明】　此题有函数的奇偶性，周期性，还和方程的根联系在一起.有一定的综合性.

【例5】（07年北京）对于函数①f(x)=lg(x-2+1),②f(x)=(x-2)²,③f(x)=cos(x+2),判断如下三个命题的真假：

命题甲：f(x+2)是偶函数；

命题乙：f(x)在（-∞，2）上是减函数，在（2，+∞）上是增函数；

命题丙：f(x+2)-f(x)在（-∞，+∞）上是增函数.

能使命题甲、乙、丙均为真的所有函数的序号是

A．①③　　　　　　　　　  B.①②

C.③　　　　　　　　　　　  D.②

【解析】 ①不满足丙，排除A、B.③不满足甲，C排除.

答案为D.

【说明】 三个函数综合在一块考查了它们性质，可谓是题小量不小啊.

二、函数的性质及图象变换多以选择题形式出现，并且低难度和高难度的试题都有可能出现.

【例6】（07年广东）客车从甲地以60km/h的速度行驶1小时到达乙地，在乙地停留了半小时，然后以80 km/h的速度行驶1小时到达丙地，下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程s与时间t之间的关系图象中，正确的是　　　　　 (　　)

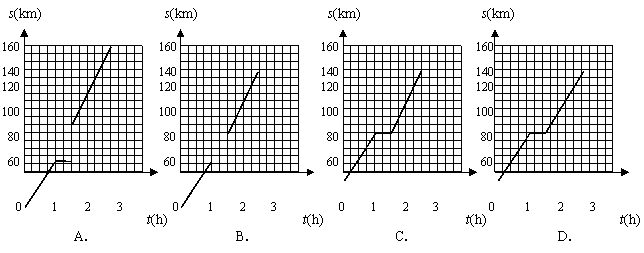
【解析】　客车共走140 km,用时2.5 h，因此排除A、D，而B中在乙地休息时没有显示出来.答案为C.

【说明】　此题以图象说明路程—时间的关系，只要图看仔细了，应该不会出错.属于低难度题.

【例7】（07年湖北）为了预防流感，某学校对教室用药熏消毒法进行

消毒. 已知药物释放过程中，室内每立方米空气中的含药

量y（毫克）与时间t（小时）成正比；药物释放完毕后，

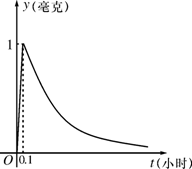y与t的函数关系式为（a为常数），

如图所示，根据图中提供的信息，回答下列问题：

（Ⅰ）从药物释放开始，每立方米空气中的含

药量y（毫克）与时间t（小时）之间的函数关系式

为　　　　　　  .

（Ⅱ）据测定，当空气中每立方米的含药量降低

到0.25毫克以下时，学生方可进教室，那从药物释放

开始，至少需要经过　　　小时后，学生才能回到教室.

【分析】（Ⅰ）两曲线交于点（0.1，1），故t∈（0，0.1]时，y=10t；t∈[0.1，+∞）时，将（0.1，1）代入，得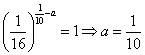故所求函数关系为：

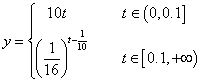
（Ⅱ）由（Ⅰ）知：当t∈[0.1，+∞）时，y为t的减函数.

令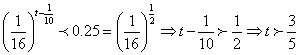.即小时，也就是36分钟后，学生才能回到教室.

【说明】　此题考查了数学建模在实际问题上的应用.有一定的区分度.

三、　　　　　　 函数的解答题，综合性较强，难度较大，要进行周密地分析、准确地计算来解决.

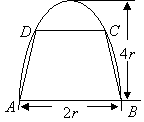【例8】 （07年北京） 如图，有一块半椭圆形钢板，其半轴长

为，短半轴长为，计划将此钢板切割成等腰梯形的形状，下

底是半椭圆的短轴，上底的端点在椭圆上，记，梯形面积为．

（I）求面积以为自变量的函数式，并写出其定义域；

（II）求面积的最大值．

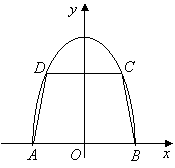【解答】（I）依题意，以的中点为原点建立直角坐标系（如图），则点的横坐标为．点的纵坐标满足方程，

解得，，

所以，

　　　 ，定义域为．

（II）记，

则，．

令，得．

因为当时，；当时，，

所以 是的最大值．

因此，当时，也取得最大值，最大值为．

即梯形面积的最大值为．

【说明】　该题以椭圆为载体，以函数思想为灵魂，以不等式、导数、三角函数等为工具，非常自然地将解析几何与导数、函数、方程、不等式、三角函数等重要数学基础知识有机交汇融为一体，无矫揉造作之嫌，是近年来较为成功的试题之一．

【例9】　(07年上海) 已知函数，常数．

　　（1）讨论函数的奇偶性，并说明理由；

　　（2）若函数在上为增函数，求的取值范围．

【解答】　（1）当时，，

对任意，，

 为偶函数．　

　　当时，，

　　取，得 ，　

　　，

　　 函数既不是奇函数，也不是偶函数．　

　　（2）解法一：设，

　　，　

　　要使函数在上为增函数，必须恒成立．

　　，即恒成立． 

　　又，．

　　的取值范围是．

　　解法二：当时，，显然在为增函数． 

当时，反比例函数在为增函数，

在为增函数．　

当时，同解法一．

【说明】　本题考查了函数的性质问题，尤其是单调性的定义法证明更要引起注意.