高三数学综合练习
一.选择题(本大题共8小题,每小题5分,共40分.)
1.![]() 等于( )
等于( )
A.2
B.![]() C.
C.![]() D.
D.![]()
2.若条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若![]()
![]() ,且
,且![]() 是定义在
是定义在![]() 上的减函数,则
上的减函数,则![]() 的图象是( )
的图象是( )
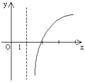
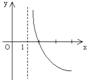
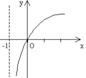
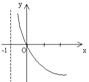
A B C D
4.某班上午要上语文、数学、英语、体育各一节,体育课既不在第一节也不在第四节,共有不同的排法数为( )
A.24 B.22 C.20 D.12
5.已知双曲线![]()
![]() ,
,![]() 的离心率为2,点
的离心率为2,点![]() ,
,![]() ,若原点到直线
,若原点到直线![]() 的距离为
的距离为![]() ,则该双曲线两准线间的距离等于(
)
,则该双曲线两准线间的距离等于(
)
A.![]() B.
B.![]() C.2 D.1
C.2 D.1
6.若底面边长为![]() 的正四棱锥的全面积与棱长为
的正四棱锥的全面积与棱长为![]() 的正方体的全面积相等,那么这个正四棱锥的侧棱与底面所成角的余弦值为( )
的正方体的全面积相等,那么这个正四棱锥的侧棱与底面所成角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设向量![]() ,
,![]() ,若
,若![]()
![]() ,且
,且![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
8.在数列![]() 中,对任意
中,对任意![]() ,都有
,都有![]() (
(![]() 为常数),则称
为常数),则称![]() 为“等差比数列”.下面对“等差比数列”的判断:
为“等差比数列”.下面对“等差比数列”的判断:
⑴ ![]() 不可能为0;
不可能为0;
⑵ 等差数列一定是等差比数列;
⑶ 等比数列一定是等差比数列;
⑷ 通项公式为![]()
![]() ,
,![]() 的数列一定是等差比数列.
的数列一定是等差比数列.
其中正确的判断为( )
A.⑴⑵ B.⑵⑶ C.⑶⑷ D.⑴⑷
二.填空题(本大题共6个小题,每小题5分,共30分.)
9.函数![]() 的定义域为________________________.
的定义域为________________________.
10.将正方形ABCD沿对角线BD折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
⑴ AC⊥BD; ⑵ △ACD是等边三角形;
⑶ AB与平面BCD所成的角为60° ⑷ AB与CD所成的角为60°
其中正确结论的序号是__________.(写出所有你认为正确的结论的序号)
11.设实数![]() ,
,![]() 满足约束条件
满足约束条件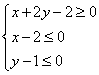 ,则
,则![]() 的最大值与最小值的和是_____________.
的最大值与最小值的和是_____________.
12.设![]() 是
是![]()
![]() 的展开式中
的展开式中![]() 项的系数,则
项的系数,则![]() _______;数列
_______;数列![]() 的前
的前![]() 项和为_____________.
项和为_____________.
13.过圆![]() 内的点
内的点![]() 作直线
作直线![]() 交圆于
交圆于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的倾斜角为
的倾斜角为![]() ,则弦
,则弦![]() 的长为________;弦
的长为________;弦![]() 中点的轨迹方程为__________.
中点的轨迹方程为__________.
14.数列![]() 的通项公式是
的通项公式是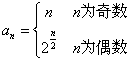 ,则数列的前
,则数列的前![]() (
(![]() 为正整数)项和是____________________.
为正整数)项和是____________________.
三.解答题(本大题共6个小题,共80分)
15.本小题满分12分
在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为角
分别为角![]() 、
、![]() 、
、![]() 的对边,且
的对边,且![]() .
.
⑴ 求![]() 的值;
的值;
⑵ 若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
16.本小题满分13分
甲、乙两人参加奥运知识竞赛,假设甲、乙两人答对每题的概率分别为![]() 和
和![]() ,且答对一题得1分,答不对得0分.
,且答对一题得1分,答不对得0分.
⑴ 甲、乙两人各答一题,求两人得分之和![]() 的分布列及数学期望;
的分布列及数学期望;
⑵ 甲、乙两人各答两题,每人每答一题记为一次,求这四次答题中至少有一次答对的概率.
17.本小题满分14分
已知定义域为![]() 的函数
的函数![]() 在区间
在区间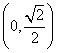 内是增函数.
内是增函数.
⑴ 求实数![]() 的取值范围;
的取值范围;
⑵ 若![]() 的极小值为
的极小值为![]() ,求实数
,求实数![]() 的值.
的值.
18.本小题满分14分
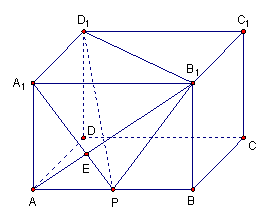
在长方体![]() 中,点
中,点![]() 为棱
为棱![]() 的中点,且
的中点,且![]() ,
,![]() ,
,![]() .
.
⑴ 求证:![]() 平面
平面![]() ;
;
⑵ 求二面角![]() 的正切值;
的正切值;
⑶ 求点![]() 到平面
到平面![]() 的距离.
的距离.
19.本小题满分13分
设![]() 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为![]() ,且对于所有的正整数n,有
,且对于所有的正整数n,有![]() .
.
⑴ 写出数列![]() 的三项;
的三项;
⑵ 求数列![]() 的通项公式,并写出推证过程;
的通项公式,并写出推证过程;
⑶ 令![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
20.本校题满分14分
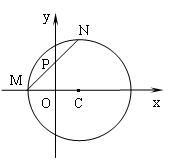
如图,已知圆C:![]() ,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
⑴ 当![]() 时,求满足条件的P点的坐标;
时,求满足条件的P点的坐标;
![]() ⑵ 当
⑵ 当![]() 时,求点N的轨迹G的方程;
时,求点N的轨迹G的方程;
⑶ 已知经过点![]() 的直线l与⑵中轨迹G相交于两个不同的点E、F,且
的直线l与⑵中轨迹G相交于两个不同的点E、F,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.