高考数学集合与简易逻辑复习材料1
今天,我怕谁之一回归课本
命题趋与应试策略
1.有关集合的高考试题.考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用文氏图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练.
2.有关“充要条件”、命题真伪的试题.主要是对数学概念有准确的记忆和深层次的理解.
试题以选择题、填空题为主,难度不大,要求对基本知识、基本题型,求解准确熟练.
1.(1)设P、Q为两个非空实数集合,定义集合P+Q=![]() ,若
,若![]() ,
,![]() ,则P+Q中元素的有________个。
,则P+Q中元素的有________个。
(2) 若![]() ,求集合A中所有元素之和 。
,求集合A中所有元素之和 。
(3)非空集合![]() ,且满足“若
,且满足“若![]() ,则
,则![]() ”,这样的
”,这样的![]() 共有_____个
共有_____个
2.(1)集合![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]() =______.
=______.
(2)已知集合![]() ,若
,若![]() ,则
,则![]() 的取值范围是( ) A.
的取值范围是( ) A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(3)设a1,b1,c1,a2,b2,c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N,那么“![]() ”是“M=N”的
”是“M=N”的
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件
(4)已知集合P=![]() ,Q=
,Q=![]() ,若Q
,若Q![]() P,则实数m的值为( )
P,则实数m的值为( )
 A 1 B
1,-1 C -1
D 0,1,-1
A 1 B
1,-1 C -1
D 0,1,-1
3.(1)满足![]() 集合M有______个。 (答:7)
集合M有______个。 (答:7)
(2)已知集合A={1,2,3,4},那么A的真子集的个数是( )
A.15 B.16 C.3 D.4
(3)满足条件M∪{1}={1,2,3}的集合M的个数是( )
A.4 B.3 C.2 D.1
4.(1)设全集![]() ,若
,若![]() ,
,![]() ,
,![]() ,则A=_____,B=___.
,则A=_____,B=___.
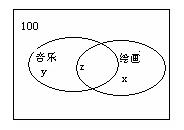
(2)某高级中学高三特长班有100名学生,其中学绘画的学生67人,学音乐的学生45人,而学体育的学生既不能学绘画,又不能学音乐,人数是21人,那么同时学绘画和音乐的学生有 人?
5.(1)设集合![]() ,集合N=
,集合N=![]() ,则
,则![]() ___
___
(2).已知![]() ,
,![]() ,则有( )
,则有( )
(A) ![]() (B) A
(B) A![]() B (C) B
B (C) B![]() (D)
(D) ![]()
(3).设集合![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
6.(1)设集合P=![]() ,
,![]() ,那么
,那么![]() 的取值范围
的取值范围
(2)已知函数![]() 在区间
在区间![]() 上至少存在一个实数
上至少存在一个实数![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(3)设集合![]() ,
,![]() 。求字母a的范围
。
。求字母a的范围
。
(4) 设集合![]() ,
,![]() 。求字母a的范围
。求字母a的范围
(5) 已知关于![]() 的取值范围 。
的取值范围 。
7.(1) 设p:![]() ;q:
;q:![]() ,则非q是p的 ( )
,则非q是p的 ( )
(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件
(2)函数![]() 在区间[1,2]存在反函数的充分不必要条件是( )
在区间[1,2]存在反函数的充分不必要条件是( )
A、![]() 或
或![]() B、
B、![]() C、a=1 D、
C、a=1 D、![]()
友情提示
1.集合元素具有确定性、无序性和互异性. 在求有关集合问题时,尤其要注意元素的互异性,
2.遇到![]() 时,你是否注意到“极端”情况:
时,你是否注意到“极端”情况:![]() 或
或![]() ;同样当
;同样当![]() 时,你是否忘记
时,你是否忘记![]() 的情形?要注意到
的情形?要注意到![]() 是任何集合的子集,是任何非空集合的真子集。
是任何集合的子集,是任何非空集合的真子集。
3.对于含有![]() 个元素的有限集合
个元素的有限集合![]() ,其子集、真子集、非空子集、非空真子集的个数依次为
,其子集、真子集、非空子集、非空真子集的个数依次为![]()
![]()
![]()
![]()
4.集合的运算性质: ⑴![]() ; ⑵
; ⑵![]() ;⑶
;⑶![]()
![]() ; ⑷
; ⑷![]() ;
;
5. 研究集合问题,一定要理解集合的意义――抓住集合的代表元素。如:![]() —函数的定义域;
—函数的定义域;![]() —函数的值域;
—函数的值域;![]() —函数图象上的点集。
—函数图象上的点集。
6. 数轴和韦恩图是进行交、并、补运算的有力工具,在具体计算时不要忘了集合本身和空集这两种特殊情况,补集思想常运用于解决否定型或正面较复杂的有关问题。
7.复合命题真假的判断。“或命题”的真假特点是“一真即真,要假全假”;“且命题”的真假特点是“一假即假,要真全真”;“非命题”的真假特点是“真假相反”。
8.四种命题及其相互关系。若原命题是“若p则q”,则逆命题为“若q则p”;否命题为“若﹁p 则﹁q” ;逆否命题为“若﹁q 则﹁p”。
提醒:(1)互为逆否关系的命题是等价命题,即原命题与逆否命题同真、同假;逆命题与否命题同真同假。但原命题与逆命题、否命题都不等价;
(2)在写出一个含有“或”、“且”命题的否命题时,要注意“非或即且,非且即或”;
(3)要注意区别“否命题”与“命题的否定”:否命题要对命题的条件和结论都否定,而命题的否定仅对命题的结论否定;
(4)对于条件或结论是不等关系或否定式的命题,一般利用等价关系“![]() ”判断其真假,这也是反证法的理论依据。(5)哪些命题宜用反证法? 1.(1)(答:8)(2) -3或
”判断其真假,这也是反证法的理论依据。(5)哪些命题宜用反证法? 1.(1)(答:8)(2) -3或![]() (3)(答:7)2.(1)(答:
(3)(答:7)2.(1)(答:![]() )(2)B. (3)D(4)D 3.(1)(答:7)4.(1)(答:
)(2)B. (3)D(4)D 3.(1)(答:7)4.(1)(答:![]() ,
,![]() )(2)(33)5.(1)(答:
)(2)(33)5.(1)(答:![]() ); (2).(D)(3).(D) 6.(1)
); (2).(D)(3).(D) 6.(1)![]() (2)(答:
(2)(答:![]() )(3)
)(3)![]() 。(4)
。(4) ![]() (5)
(5) ![]() 。7.(1)(B)
。7.(1)(B)
集合与简易逻辑基本概念回归课本复习材料2
今天,我怕谁之二
8. 下列四个命题:①在空间,存在无数个点到三角形各边的距离相等;
②在空间,存在无数个点到长方形各边的距离相等;
③在空间,既存在到长方体各顶点距离相等的点,又存在到它的各个面距离相等的点;
④在空间,既存在到四面体各顶点距离相等的点,又存在到它的各个面距离相等的点.
其中真命题的序号是 .(写出所有真命题的序号)
9.(1)给出下列命题:①实数![]() 是直线
是直线![]() 与
与![]() 平行的充要条件;②若
平行的充要条件;②若![]() 是
是![]() 成立的充要条件;③已知
成立的充要条件;③已知![]() ,“若
,“若![]() ,则
,则![]() 或
或![]() ”的逆否命题是“若
”的逆否命题是“若![]() 或
或![]() 则
则![]() ”;④“若
”;④“若![]() 和
和![]() 都是偶数,则
都是偶数,则![]() 是偶数”的否命题是假命题 。其中正确命题的序号是_______
是偶数”的否命题是假命题 。其中正确命题的序号是_______
(2)设命题p:![]() ;命题q:
;命题q:![]() 。若┐p是┐q的必要而不充分的条件,则实数a的取值范围是
。若┐p是┐q的必要而不充分的条件,则实数a的取值范围是
(3)设集合![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分又不必要条件
(4) ![]() 至少有一个负的实根的必要非充分条件是( )
至少有一个负的实根的必要非充分条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]() 或
或![]()
( 5)对于![]() 的一切值,
的一切值,![]() 是使
是使![]() 恒成立的( )
恒成立的( )
A 充分不必要条件B必要不充分条件 C 充分必要条件 D 既不充分也不必要条件
(6) ![]() 是
是![]() 的( )
的( )
A 充分不必要条件B必要不充分条件 C 充分必要条件 D 既不充分也不必要条件
(7) “a=1”是“函数y=cos2ax-sin2ax的最小正周期为π”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分条件也非必要条件
10.已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集为_______
的解集为_______
11.解关于![]() 的不等式:
的不等式:![]() 。
。
12.(1)![]() 对一切
对一切![]() 恒成立,则
恒成立,则![]() 的取值范围是_______;
的取值范围是_______;
(2)关于![]() 的方程
的方程![]() 有解的条件是什么?(答:
有解的条件是什么?(答:![]() ,其中
,其中![]() 为
为![]() 的值域),特别地,若在
的值域),特别地,若在![]() 内有两个不等的实根满足等式
内有两个不等的实根满足等式![]() ,则实数
,则实数![]() 的范围是_______.
的范围是_______.
13.实系数方程![]() 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则![]() 的取值范围是_________
的取值范围是_________
14.若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,其中
,其中![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集为________
的解集为________
友情提示
9.充要条件。
关键是分清条件和结论(划主谓宾),由条件可推出结论,条件是结论成立的充分条件;由结论可推出条件,则条件是结论成立的必要条件。从集合角度解释,若![]() ,则A是B的充分条件;若
,则A是B的充分条件;若![]() ,则A是B的必要条件;若A=B,则A是B的充要条件。
,则A是B的必要条件;若A=B,则A是B的充要条件。
10. 一元一次不等式的解法:通过去分母、去括号、移项、合并同类项等步骤化为![]() 的形式,
的形式,
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ;若
;若![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
11. 一元二次不等式的解集(联系图象)。尤其当![]() 和
和![]() 时的解集你会正确表示吗?设
时的解集你会正确表示吗?设![]() ,
,![]() 是方程
是方程![]() 的两实根,且
的两实根,且![]() ,则其解集如下表:
,则其解集如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| R |
|
|
|
| R | R |
|
|
12. 对于方程![]() 有实数解的问题。首先要讨论最高次项系数
有实数解的问题。首先要讨论最高次项系数![]() 是否为0,其次若
是否为0,其次若![]() ,则一定有
,则一定有![]() 。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?
。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?
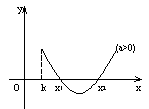
13.一元二次方程根的分布理论。方程![]() 在
在![]() 上有两根、在
上有两根、在![]() 上有两根、在
上有两根、在![]() 和
和![]() 上各有一根的充要条件分别是什么?
上各有一根的充要条件分别是什么?
 (
(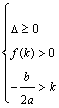 、
、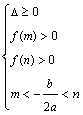 、
、![]() )。根的分布理论成立的前提是开区间,若在闭区间
)。根的分布理论成立的前提是开区间,若在闭区间![]() 讨论方程
讨论方程![]() 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间![]() 上实根分布的情况,得出结果,再令
上实根分布的情况,得出结果,再令![]() 和
和![]() 检查端点的情况.
检查端点的情况.
14.二次方程、二次不等式、二次函数间的联系你了解了吗?二次方程![]() 的两个根即为二次不等式
的两个根即为二次不等式![]() 的解集的端点值,也是二次函数
的解集的端点值,也是二次函数![]() 的图象与
的图象与![]() 轴的交点的横坐标。8.
9.(1)(答:①④);(2)(答:
轴的交点的横坐标。8.
9.(1)(答:①④);(2)(答:![]() )(3)B.(4) B.( 5)B(6) B (7) A. 10.(答:
)(3)B.(4) B.( 5)B(6) B (7) A. 10.(答:![]() )11.(答:当
)11.(答:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() )12.(1)(答:
)12.(1)(答:![]() );(2)(答:
);(2)(答:![]() )13.(答:(
)13.(答:(![]() ,1)) 14.(答:
,1)) 14.(答:![]() )
)