直线方程
一. 教学内容:
直线方程
二. 重点、难点:
1. 直线方程:
点斜式:![]()
斜截式:![]()
两点式:![]()
截距式:![]()
一般式:![]()
参数式: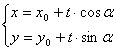
![]() 为参数
为参数
2. ![]()
![]()
![]()
![]()
![]()
夹角为![]() :
:![]()
【典型例题】
[例1] 直线![]() 不过第二象限,求
不过第二象限,求![]() 的取值范围。
的取值范围。
解:(1)![]()
![]()
![]()
![]()
(2)![]()
![]()
![]() 成立
成立
(3)![]()
![]()
![]() 不成立
不成立
∴ ![]()
[例2] 已知直线![]() 在
在![]() 轴的截距比在
轴的截距比在![]() 轴上的截距大1,且过定点
轴上的截距大1,且过定点![]() ,求
,求![]() 的方程。
的方程。
解:设![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∴
∴ ![]()
![]()
[例3] 直线![]() 倾斜角为
倾斜角为![]() ,若它与两坐标轴围成三角形的面积为6,求
,若它与两坐标轴围成三角形的面积为6,求![]() 的方程。
的方程。
解:![]()
![]()
![]()
∴ ![]()
![]()
![]()
![]() ∴
∴ ![]()
[例4] ![]()
![]()
(1)![]() 求
求![]() ;(2)
;(2)![]() 求
求![]()
解:
(1)![]()
![]()
![]()
![]() 或
或![]()
(2)![]()
![]()
![]() 或
或![]()
[例5] 已知三条直线:![]() ,
,![]() ,
,![]() 交于一点,求
交于一点,求![]()
解:显然![]() ,
, 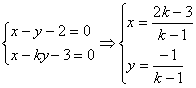
代入![]()
![]() ∴
∴ ![]()
[例6] ![]() ,
,![]() ,
,![]() ,
,![]()
(1)在![]() 上求一点P,使
上求一点P,使![]() 最小;
最小;
(2)在![]() 上求一点Q,使
上求一点Q,使![]() 最大。
最大。
解:(1)B关于![]() 的对称
的对称![]()
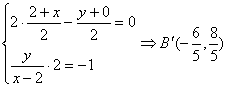
![]()
(2)![]()
![]()
[例7] 过点![]() 与直线
与直线![]() ,
,![]() 的夹角相等的直线。
的夹角相等的直线。
解: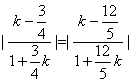
![]()
![]()
![]()
![]()
![]()
![]()
∴ ![]()
![]()
∴ ![]()
![]()
[例8] 过点![]() 作两条互相垂直线分别交
作两条互相垂直线分别交![]() 轴正半轴于A、B。若四边形的面积被AB平分,求直线AB。
轴正半轴于A、B。若四边形的面积被AB平分,求直线AB。
解:设![]()
![]() ∴
∴ ![]() ,
,![]()
![]() 即
即![]()
![]()
![]()
![]()
(1)![]() 或
或![]()
(2)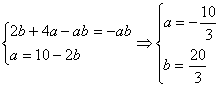 (舍)
(舍)
∴ ![]() 或
或![]()
[例9] ![]() ,
,![]() ,A在
,A在![]() 轴负半轴上,问A在何处
轴负半轴上,问A在何处![]() 有最大值?
有最大值?
解:设![]()
![]() ∴
∴ ![]()
![]()
![]()
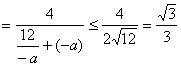
![]()
![]() 时,
时,![]() 最大
最大![]()
[例10] ![]() ,
,![]() 在
在![]() 轴上,C在直线
轴上,C在直线![]() 上,求
上,求![]() 的周长的最小值。
的周长的最小值。
解:A关于![]() 的对称点为
的对称点为![]() ,A关于
,A关于![]() 轴的对称点为
轴的对称点为![]()
![]() 周长最小值为
周长最小值为![]() ,此时
,此时![]() ,
,![]()
[例11] 已知![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 。
。
解:![]()
![]()
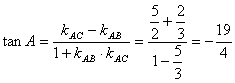
![]()
[例12] 正![]() 中,
中,![]() ,中心
,中心![]() ,求三边所在直线。
,求三边所在直线。
解:设AM交BC于D M分![]() 比
比![]() ∴
∴ ![]()
![]() ∴
∴ ![]() ∴
∴ ![]()
![]() 与AD夹角为
与AD夹角为![]()
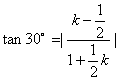
![]() ∴
∴ ![]()
![]()
[例13] ![]() 中
中![]() ,
,![]() ,内心
,内心![]() ,求C。
,求C。
解:![]() ,
,![]() ,
,![]() ∴
∴ ![]()
![]()
![]()
![]()
A关于![]() 的对称点为
的对称点为![]()
![]()
![]() ∴
∴ ![]()
[例14] ![]() 中
中![]() ,两条中线
,两条中线![]() ,
,![]() ,求
,求![]() 。
。
解:A不在中线上,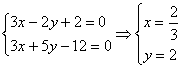 重心
重心![]()
BC边中比为AD ∴ ![]() 分
分![]() 之比
之比![]()
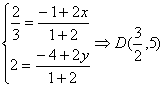
设![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]()
【模拟试题】(答题时间:40分钟)
1. 过![]() 横纵截距相等的直线
横纵截距相等的直线![]() 的方程。
的方程。
2. 将直线![]() 绕它上面一点
绕它上面一点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 的
的![]() ,求
,求![]() 的方程。
的方程。
3. 过点![]() 作直线
作直线![]() 与已知直线
与已知直线![]() ,
,![]() 分别交于M、N,点A恰为MN中点,求
分别交于M、N,点A恰为MN中点,求![]() 的方程。
的方程。
4. 直线![]() 过点
过点![]() 与两点A、B等距,已知
与两点A、B等距,已知![]() ,
,![]() ,求
,求![]() 的方程。
的方程。
5. 一直线过点![]() ,它被平行直线
,它被平行直线![]() ,
,![]() 所截的线段中点在
所截的线段中点在![]() 上,求
上,求![]() 。
。
6. 正方形中心![]() ,一边所在直线方程为:
,一边所在直线方程为:![]() ,求其余三边所在直线方程。
,求其余三边所在直线方程。
【试题答案】
1. 解:
(1)过![]()
![]()
(2)不过![]()
![]()
![]()
2. 解:
![]() 的倾斜角为
的倾斜角为![]()
![]()
![]()
![]()
3. 解:
设![]() ,
,![]()
![]()
![]()
4. 解:
![]()
![]() 中点
中点![]()
∴ ![]()
![]()
![]()
![]()
5. 解:
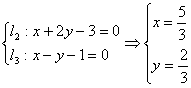
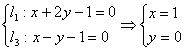 中点
中点![]()
∴ ![]()
6. 解:
不妨设正方形ABCD ![]()
![]()
设![]()
![]()
![]()
∴ ![]()
设![]() 、
、![]() 为:
为:![]()
![]()
![]()
![]() 或
或![]()
∴ ![]() 、
、![]() 为:
为:![]() 、
、![]()