直线综合练习与解答
一. 教学内容:
直线综合练习与解答
【模拟试题】
一. 选择:
1. 点![]() ,
,![]() ,
,![]() 且
且![]() 是线段
是线段![]() 上一点
上一点![]() ,则直线
,则直线![]() 斜率
斜率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D. ![]()
![]()
2. 菱形![]() 的一边
的一边![]() 所在直线方程为
所在直线方程为![]() ,一对角线端点为
,一对角线端点为![]() 、
、![]() 则点
则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知三角形的两边所在直线的方程分别为![]() ,
,![]() ,第三边中点为
,第三边中点为![]() ,则第三条边所在直线方程为( )
,则第三条边所在直线方程为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D. ![]()
4. 通过点![]() 的直线与坐标轴所围成的三角形面积等于
的直线与坐标轴所围成的三角形面积等于![]() ,这样的直线共有( )
,这样的直线共有( )
A. 1条 B. 2条 C. 3条 D. 4条
5. 下列不等式组的整数解有( )个
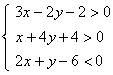
A. 4 B. 5 C. 6 D. 7
6. 过![]() 与原点距离最远的直线方程为( )
与原点距离最远的直线方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7. 已知![]()
![]() 在直线
在直线![]() :
:![]() 上找一点
上找一点![]() 使
使![]() 最小,则最小值为( )
最小,则最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 已知![]() ;
;![]() 的最小值为( )
的最小值为( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
9. 直线![]() 、
、![]() 的交点在第一象限,则
的交点在第一象限,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
10. 已知
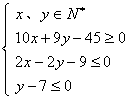 则
则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二. 解答题:
1. ![]() 为何值时下面三条直线
为何值时下面三条直线![]() ,
,![]() ,
,![]() 不能构
不能构
成三角形。
2. 集合![]() ,
,![]() ,
,![]()
(1)![]() 为何值时,
为何值时,![]() 有且仅有两个元素
有且仅有两个元素
(2)![]() 为何值时,
为何值时,![]() 有且仅有三个元素
有且仅有三个元素
3. 某家具公司生产木制桌椅,需木工,漆工两道工序,已知木工4小时作一把椅子,8小时作一张桌子,漆工漆一把椅子2小时,一张桌子1小时,该公司有木工160人,每人每星期工作50小时,漆工26人,每人每星期工作50小时,一把椅子利润15元,一张桌子利润20,问应如何安排生产,可使公司获利最大。
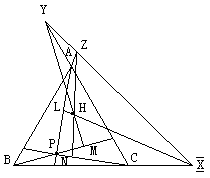
4.(选作)![]() 为
为![]() 垂心,
垂心,![]() 为
为![]() 内任一点,
内任一点,![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,求证
,求证![]() 、
、![]() 、
、![]() 三点共线。
三点共线。
【试题答案】
一. 选择:
1. D 2. A 3. B 4. D 5. C
6. A 7. B 8. C 9. B 10. D
二. 解答题
1. 解(1)交于一点
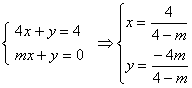 代入
代入![]()
∴ ![]() 或
或![]()
(2)![]() ∥
∥![]()
(3)![]() ∥
∥![]()
![]()
(4)![]() ∥
∥![]() 无解
无解
∴ ![]()
2. 解:![]() 为过点
为过点![]() 的直线
的直线 ![]() 为过点
为过点![]() 的直线
的直线 ![]() 为半径圆
为半径圆
(1)![]() 时
时![]() 时
时
(2)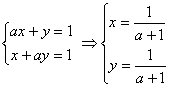 代入
代入
![]()
∴ ![]()
3. 设生产椅子![]() 把,桌子
把,桌子![]() 张
张
约束条件:
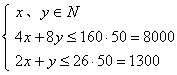
目标函数![]()
在![]() 时
时 ![]() 元
元
4. 设以![]() 为原点建立直角坐标系
为原点建立直角坐标系![]() ,
,![]() ,
,![]()
![]()
(1)∴ ![]() ∴
∴ ![]()
∴ ![]() ①
① ![]()
∴ ![]()
∴ ![]() ②
②
即:![]()
![]() 过
过![]() ∴
∴ ![]()
②同①![]()
![]()
![]()
①+②![]()
![]()
![]() 在
在![]() 上
上
同之![]() ,
,![]() 在
在![]() 上 ∴
上 ∴![]() 、
、![]() 、
、![]() 三点共线
三点共线