直线
一. 教学内容:
直线
二. 知识要点:
(一)直线的倾斜角(![]() )和斜率(
)和斜率(![]() )
)
1. 定义 倾斜角范围![]() 斜率:
斜率:![]()
2. ![]() 与
与![]() 的关系:
的关系: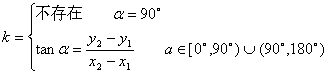

注:准确地把握这两个概念,关注斜率![]() 不存在带来的问题。
不存在带来的问题。
[例] (1)直线![]() 的斜率
的斜率![]() ,倾斜角
,倾斜角![]() 。
。
(2)若![]() ,则直线
,则直线![]() 的斜率 ,倾斜角 。
的斜率 ,倾斜角 。
拓展:取消![]() 的限制,结论如何。
的限制,结论如何。
(3)直线L过点![]() 且与以
且与以![]() ,
,![]() 为端点的线段PQ相交,则斜率的取值范围 ,倾斜角的取值范围 。
为端点的线段PQ相交,则斜率的取值范围 ,倾斜角的取值范围 。
(4)若![]() ,则
,则![]() 。
。
(5)若![]() 时,则
时,则![]() 。
。
答案:(1)![]() ;
;![]() (2)
(2)![]() ;
;![]()
(3)![]() ;
;![]()
(4)![]() (5)
(5)![]()
(二)直线方程
1. 直线方程的五种形式及适用范围
(1)斜截式:![]() 不含与
不含与![]() 轴垂直的直线
轴垂直的直线
(2)点斜式:![]() 不含与
不含与![]() 轴垂直的直线
轴垂直的直线
(3)两点式:![]() 不含与
不含与![]() 轴、
轴、![]() 轴垂直的直线
轴垂直的直线
(4)截矩式:![]() 不含过原点和与
不含过原点和与![]() 轴、
轴、![]() 轴垂直的直线
轴垂直的直线
(5)一般式:![]() 无限制(可表示任何直线)
无限制(可表示任何直线)
注:两点式的“改良”![]() 可表示任何直线。
可表示任何直线。
2. 直线系:
(1)平行直线系:![]() (
(![]() 为待定系数,斜率
为待定系数,斜率![]() 已知)
已知)
(2)过定点直线系:![]() (
(![]() 为待定系数,点
为待定系数,点![]() 为已知)
为已知)
(3)过两直线交点的直线系:已知![]() ;
;![]() ,则
,则![]() (
(![]() 为参数——待定系数)
为参数——待定系数)
L是过![]() 与
与![]() 交点的直线系 (不含
交点的直线系 (不含![]() )
)
若![]() ,则L是与
,则L是与![]() 与
与![]() 平行的直线系。
平行的直线系。
注:(1)与已知直线![]() 平行的直线系:
平行的直线系:![]() (
(![]() 为参数)
为参数)
(2)与已知直线![]() 垂直的直线系:
垂直的直线系:![]() (
(![]() 为参数)
为参数)
(三)两条直线的位置关系
1. 判定两条直线的位置关系(三种:相交、平行、重合)
设![]() ;
;![]()
![]() ;
;![]()
(1)![]() 或仅有一个不存在
或仅有一个不存在![]()
![]() 或一个为零一个不存在
或一个为零一个不存在![]()
(2)![]() 且
且![]() 或
或![]() 均不存在
均不存在![]() 且
且![]()
![]()
(3)![]() 与
与![]() 重合
重合![]() 且
且![]() 或
或![]() 均不存在
均不存在![]() 且
且![]()
![]()
[例题] 已知两直线![]() ;
;![]() ,当
,当![]() 为何值时,
为何值时,![]() 与
与![]() (1)相交(2)平行(3)重合
(1)相交(2)平行(3)重合
解:当![]() 时,则
时,则![]() ∴
∴ ![]()
(1)当![]() 时,
时,![]() ;
;![]() ∴
∴ ![]()
(2)当![]() 时,
时,![]() ;
;![]() ∴
∴ ![]()
(3)当![]() 时,
时,![]() ;
;![]() ∴
∴ ![]() 重合
重合
(4)当![]() ,
,![]() ,
,![]() 时,相交。
时,相交。
说明:![]() 时,
时,![]() 与
与![]() 平行或重合相交且只有有数几个值应先分析。
平行或重合相交且只有有数几个值应先分析。
2. 两条直线所成的角(夹角)与直线![]() 到
到![]() 的角
的角
夹角:![]()
![]() 到
到![]() 的角:
的角:![]()
3. 点到直线的距离:![]()
![]() 到
到![]() 的距离为
的距离为![]() ;
;![]() 到
到![]() 的距离为
的距离为![]() ,两条平行线
,两条平行线![]() ;
;![]() ,则
,则![]() 与
与![]() 的距离
的距离![]()
(四)对称性问题(专题)方法——相关点法
1. 对称分两大类
(1)关于点中心对称:点![]() 关于定点
关于定点![]() 中心对称点
中心对称点![]()
(2)关于直线轴对称:点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则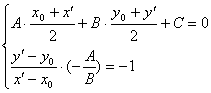 解出
解出![]() 的值为:
的值为: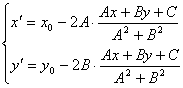
2. 常用对称的规律:已知点![]() ,直线
,直线![]()
(1)关于X轴对称的对称点![]() ;
;![]()
(2)关于Y轴对称的对称点![]() ;
;![]()
(3)关于直线![]() 的对称点
的对称点![]() ;
;![]()
(4)关于直线![]() 的对称点
的对称点![]() ;
;![]()
(5)关于原点![]() 的对称点
的对称点![]() ;
;![]()
(6)关于点![]() 的对称点
的对称点![]() ;
;![]()
(7)关于直线![]() 的对称点
的对称点![]() ;
;![]()
(8)关于直线![]() 的对称点
的对称点![]() ;
;![]()
(9)关于直线![]() 的对称点
的对称点![]() ;
;![]()
(10)关于直线![]() 的对称点
的对称点![]() ;
;![]()
思考:我们注意到只须将对称点的坐标Q代入直线L即得对称的直线方程,为什么?
它们的理论依据是什么?——“相关点法”
我们以(9)题为例,即求直线![]() ,关于直线
,关于直线![]() 对称的直线方程。
对称的直线方程。
解:设所求直线上任意一点![]()
关于直线![]() 的对称点
的对称点![]()
则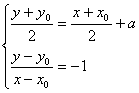 ∴
∴ 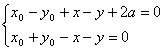 ∴
∴ 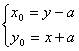
∵ ![]() ∴
∴ ![]() 即:
即:![]()
点拨:① 代入对称点坐标的理论依据是“相关点法”
② 有关对称性问题都可用“相关点法”求对称曲线。
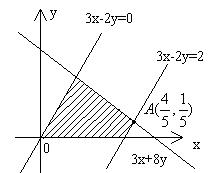
(五)线性规划
1. 二元一次不等式表示平面区域
(1)二元一次不等式![]() 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线![]()
![]() 一侧所有点组成的平面区域,直线
一侧所有点组成的平面区域,直线![]() 应画成虚线,
应画成虚线,![]() 表示直线
表示直线![]() 另一侧所有点组成的平面区域,画不等式。
另一侧所有点组成的平面区域,画不等式。![]() 所表示的平面区域时,应把边界直线画成实线。
所表示的平面区域时,应把边界直线画成实线。
(2)二元一次不等式组所表示的平面区域是各个不等式表示的平面点集的交集即各个不等式所表示的平面区域的公共部分。
快捷判断法:
(1)代点检验法
(2)直线![]() 上半平面为
上半平面为![]() 的区域;下半平面为
的区域;下半平面为![]() 的区域
的区域
2. 线性规划
(1)对于变量![]() 的约束条件,都是关于
的约束条件,都是关于![]() 的一次不等式,称为线性约束条件,
的一次不等式,称为线性约束条件,![]() 是欲达到最值所涉及的变量
是欲达到最值所涉及的变量![]() 的解析式,叫做目标函数。当
的解析式,叫做目标函数。当![]() 是关于
是关于![]() 的一次解析式时,
的一次解析式时,![]() 叫做线性目标函数。
叫做线性目标函数。
(2)求线性目标函数在线性约束条件下的最值问题称为线性规划问题,满足线性约束条件的解![]() 称为可行解。由所有解组成的集合叫可行域,使目标函数取得最值的可行解叫最优解。
称为可行解。由所有解组成的集合叫可行域,使目标函数取得最值的可行解叫最优解。
3. 求解线性规划问题的步骤是:(1)根据实际问题的约束条件列出不等式;(2)作出可行域,写出目标函数;(3)确定目标函数的最优位置,从而获得最优解。
【模拟试题】(答题时间:45分钟)
一. 选择题
1. 直线![]() 与两坐标轴围成的三角形面积为( )
与两坐标轴围成的三角形面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 若直线![]() 与直线
与直线![]() 平行,则
平行,则![]() 在两坐标轴上截距之和为( )
在两坐标轴上截距之和为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 过原点,且与直线![]() 成
成![]() 角的直线方程为( )
角的直线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]()
4. 已知![]() 为直线
为直线![]() 和
和![]() 所成的角,则当
所成的角,则当![]() 取最大值时,实数
取最大值时,实数![]() 值为( )
值为( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
5. 三条直线![]() ;
;![]() ;
;![]() 不能围成三角形,则
不能围成三角形,则![]() 取值的个数为( )
取值的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 直线![]() 过点
过点![]() ,且与以
,且与以![]() 和
和![]() 为端点的线段相交,则
为端点的线段相交,则![]() 斜率取值范围为( )
斜率取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 以上都不对
D. 以上都不对
7. 将直线![]() 沿
沿![]() 轴正向平移2个单位,再沿
轴正向平移2个单位,再沿![]() 轴负方向平移3个单位,又回到了原来的位置,则
轴负方向平移3个单位,又回到了原来的位置,则![]() 的斜率为( )
的斜率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 已知点![]() 和
和![]() 分别是直线
分别是直线![]() 上和
上和![]() 外的点,若
外的点,若![]() 方程为
方程为![]() ,则方程
,则方程![]() 表示( )
表示( )
A. 与![]() 重合的直线
B. 过
重合的直线
B. 过![]() 且与
且与![]() 垂直的直线
垂直的直线
C. 过![]() 且与
且与![]() 平行的直线 D. 不过
平行的直线 D. 不过![]() 但与
但与![]() 平行的直线
平行的直线
9. 已知点![]() ,
,![]() ,P点在直线
,P点在直线![]() 上,使
上,使![]() 最大,则P点坐标为( )
最大,则P点坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 若方程![]() 表示一条直线,则实数
表示一条直线,则实数![]() 满足( )
满足( )
A. ![]() B.
B.
![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
11. 曲线![]() 关于直线
关于直线![]() 对称的曲线方程为( )
对称的曲线方程为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
12. 函数![]() 一条对称轴为
一条对称轴为![]() ,则
,则![]() 倾斜角为( )
倾斜角为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
13. 直线![]() 与
与![]() 及坐标轴围成的四边形有外接圆,则
及坐标轴围成的四边形有外接圆,则![]() 值为( )
值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
14. ![]() 中
中![]() ,
,![]() ,且
,且![]() ,则A点轨迹方程为( )
,则A点轨迹方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D.
![]()
二. 填空题
15. 已知![]() ;
;![]()
![]() ,则
,则![]() 、
、![]() 和
和![]() 轴围成三角形面积最小值为
。
轴围成三角形面积最小值为
。
16. 过点![]() ,
,![]() 的直线与直线
的直线与直线![]() 交于P点,则P点分
交于P点,则P点分![]() 的比为
的比为
。
17. 由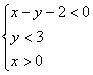 确定的可行域中,横纵坐标均为整数的点有 个。
确定的可行域中,横纵坐标均为整数的点有 个。
18. 已知集合![]() ,
,![]() ,
,![]()
![]() 且
且![]() ,则
,则![]() 中元素个数为
。
中元素个数为
。
三. 解答题
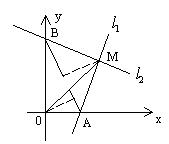
19. 过点![]() 作
作![]() 交
交![]() 正半轴于A,作
正半轴于A,作![]() 交
交![]() 正半轴于B,若
正半轴于B,若![]() ,且AB恰平分四边形OAMB面积,求直线AB方程。
,且AB恰平分四边形OAMB面积,求直线AB方程。
20. 一化工厂生产某产品,生产成本为20元/![]() ,出厂价为50元/
,出厂价为50元/![]() ,每生产1
,每生产1![]() 该产品产生
该产品产生![]() 的污水,有两种处理方式:直接排入河流或输送到污水处理厂。环保部门对排入河流污水收费为15元/
的污水,有两种处理方式:直接排入河流或输送到污水处理厂。环保部门对排入河流污水收费为15元/![]() ,污水处理厂对污水收费为5元/
,污水处理厂对污水收费为5元/![]() ,但只能净化污水的
,但只能净化污水的![]() ,未净化污水仍排入河流,且排放费仍由厂家付给,若污水处理厂处理污水最大能力为
,未净化污水仍排入河流,且排放费仍由厂家付给,若污水处理厂处理污水最大能力为![]() /分钟,环保部门允许该化工厂污水排入河流最大排放量为
/分钟,环保部门允许该化工厂污水排入河流最大排放量为![]() /分钟,问该化工厂每分钟生产多少产品,每分钟直接排入河流污水为多少时纯利润最高?
/分钟,问该化工厂每分钟生产多少产品,每分钟直接排入河流污水为多少时纯利润最高?
【试题答案】
一. 选择题
1. D 2. B 3. C 4. C 5. C 6. C 7. B 8. C 9. A 10. C
11. D 12. B 13. B 14. A
二. 填空题
15.
![]() 16.
16. ![]() 17.
17. ![]() 18.
18. ![]()
三. 解答题
19.
解:设![]() ,则
,则![]() ,
,![]()
则![]() ,
,![]()
由![]()
![]()
![]() 或
或![]()
故![]() 或
或![]()
20.
解:设每分钟生产![]() ,产生污水
,产生污水![]() ,
,![]() 排入河流,纯利润
排入河流,纯利润![]() 元
元
由已知,则有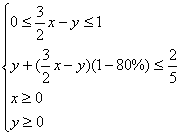 即
即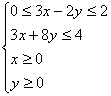
![]() 即
即![]()
利用线性规划方法可知,当![]() ,
,![]() 时,
时,![]()
所以每分钟生产![]() ,
,![]() 排入河流,纯利润最高。
排入河流,纯利润最高。