高考数学模拟考试题（文科卷3）
时量120分钟. 满分150分
一、 选择题：（本大题共10小题；每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1、将函数
的图象按向量
平移后所得图象的解析式是（ ）
A．
B．
C．
D．
2.在等差数列
中，若
，则
的值为 ( )
A．14 B．15 C．16 D．17
3．若
是常数，则“
”是“对任意
，有
”的 ( )
A．充分不必要条件. B．必要不充分条件.
C．充要条件. D．既不充分也不必要条件.
4．把函数
）的图象向左平移
个单位，再将图象上所有点的 横坐标伸长到原来的2倍（纵坐标不变），得到函数
的图象，则 （ ）
A．
B．
C．
D．
5．已知P是以F1、F2为焦点的椭圆
上一点，若
=0， 
=2，则椭圆的离心率为 （ ）
A．
B．
C．
D．
6．如果函数
的值域为R，则常数m的取值范围是（ ）
A．
B．
C．
D．
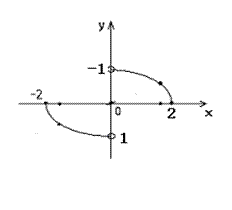7.如图,函数的图象是中心在原点,焦点在
轴上的椭圆的两段弧,则不等式
的解集为 （ ）
A.
B.
C.
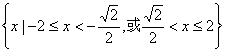D.
8设双曲线以椭圆
长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为 （ ）
A．
B．
C．
D．
9．已知向量a=（－2，2），b=（5，k）.若a+b不超过5，则k的取值范围是 （ ）
A．[－4，6] B．[－6，4] C．[－6，2] D．[－2，6]
10．已知
，则方程
不相等的实根共有 （ ）
A．5个 B．6个 C．7个 D．8个
二、填空题：（本大题共5小题，每小题4分，共20分。把答案填在题中横线上。）
11、某校要从高三的6个班中派9名同学参加市中学生外语口语演讲，每班至少派1人，则这9个名额的分配有 种（用数字作答）。
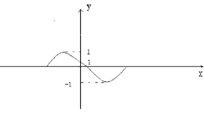
12、右图是周期为
的三角函数
的图象，那么
可以写成 。
13、已知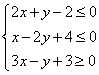
，则函数
取得最大值时 
14、一个单位有职工360人，其中业务人员276人，管理人员36人，后勤人员48人，为了了解职工的住房情况，要从中抽取一个容量为30的样本，则应取 的抽样方法，且应从后勤人员中抽取 人。
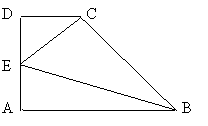
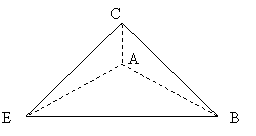
15、一直角梯形ABCD，
，E为AD中点，沿CE、BE把梯形拆成四个面都的直角三角形的三棱锥，使A、D重合，则三棱锥的体积为 。
 |  | ||
三、解答题：（本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。）
16、（本小题满分12分）已知函数
①、求函数的最小正周期和最大值；
②、该函数图象能否由的图象
按某个向量
平移得到，若能，求出满足条件的向量；若不能，说明理由。
17、（本小题满分13分）某射手在射击时，每五发子弹平均有三发子弹可射中；
①试求这名射手击n发子弹，每发都射不中的概率；
②若这个射手至少有1发射中的概率大于0.999，试问此时他必须射击多少次？（
）
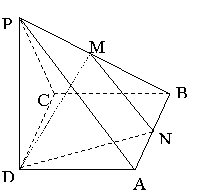
18、（本小题满分13分）已知四棱锥P—ABCD的底面是边长为4的正方形，
，PD=6，M、N分别是PB、AB的中点；
①求证： 
②求三棱锥P—DMN的体积。
19、（本小题满分13分）设函数
（
）的图象关于原点对称，且
时，
取极小值
①求
的值；
②当
时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论。
20、（本小题满分14分）已知向量
，动点M到定直线
的距离等于
，并且满足
，其中O为坐标原点，K为参数；
①求动点M的轨迹方程，并判断曲线类型；
②当K=
时，求
的最大值和最小值；
（21）（本小题满分15分）
已知等差数列{an}的公差不为零，首项
且前n项和为
。
（I）当
时，在数列{an}中找一项
，使得
成为等比数列，求m的值。
（II）当
时，若自然数
满足
并且
是等比数列，求
的值。
文科3答案
一、 选择题（每小题5分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | C | A | B | D | B | A | C | C | C |
二、填空题：（每小题4分）
11 56 ; 12 
;
13 
;
14 分层 , 4 ; 15 
;
三、解答题：（共80分）
16 解：①
当
时，
．．．．．６分
②设该图象能由的图象按向量平移得到，则有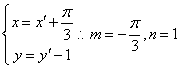
，又由
，知=
…………12分
17 解：①
子弹射中的概率为
，
射不中的概率为
每发都不中的概率为
．．．．．．．．．．．．．．．６分
②设射击n次，则
即
即至少射击8发。．．．．．．．．．．．．．．．．．．13分
18 解：（法一）①
，
………６分
②设AC、BD交于O，连接MO、PN则由①知MN//PA，
PA//平面DMN
M是PB的中点
M到平面ABCD的距离等于PD，而
……13分
（法二）①如图建立空间直角坐标系
，则
D（0，0，0），A（4，0，0），B（4，4，0）C（0，4，0），
P（0，0，6），M（2，2，3），N（4，2，0），O（2，2，0）
即
②同解法一的解法。
19 解：①函数的图象关于原点对称
对任意实数，有
．．．．．２分
即
恒成立
．．．．．４分
时，取极小值
，
且
．．．．．６分
②当时，图象上不存在这样的两点使结论成立。．．．７分
假设图象上存在两点
，使得过此两点处的切线互相垂直，则由
知两点处的切线斜率分别为
且
（*） ．．．．．．11分
[-1，1]
与（*）矛盾 ．．．．．１3分
20 解：①设
，则由，且O为原点得
A（2，0），B（2，1），C（0，1）从而
代入得
为所求轨迹方程 ．．．．．．．．５分
当K=1时，
=0 轨迹为一条直线
当K
1时，
，若K=0，则为圆
若K
，则为双曲线 ．．．．．．７分
②当K=时，若
或
则为椭圆
方程为
，即
且
．．．．．．10分
从而
．．．．．．．．．．．．．．．．．．12分
又 当
时，
取最小值
当
时，取最大值16
故
，
．．．．．14分
21 解：（I）数列{an}的公差
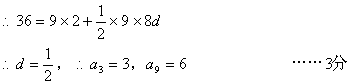
由a3，a9，am成等比数列
则
，得
又
……7分
（II）
是等差数列，
又
成等比数列，所以公比
．．．．．．11分
又
是等差数列中的项
……15分