高考数学模拟考试题（文科卷4）
时量120分钟. 满分150分
一、本题共12小题，每小题5分，共50分，在每小题给出的四个选项中只有一个选项是符合题目要求的．
1．设a、b、c是任意的非零平面向量，且相互不共线，则（ ）
①（a·b）c-（c·a）b＝0
②a-b＜a-b；
③（b·c）a-（c·a）b不与c垂直；
④（3a＋2b）·（3a-2b）＝9a
-4b．
其中的真命题是（ ）
A．②④ B．③④ C．②③ D．①②
2．若直线mx＋ny＝4和⊙O∶
没有交点，则过（m，n）的直线与椭圆
的交点个数（ ）
A．至多一个 B．2个
C．1个 D．0个
3．将正方形ABCD沿对角线BD折成120°的二面角，C点到
处，这时异面直线AD与
所成角的余弦值是（ ）
A．
B．
C．
D．
4．现用铁丝做一个面积为1平方米、形状为直角三角形的框架，有下列四种长度的铁丝各一根供选择，其中最合理（即够用，浪费最少）的一根是（ ）．
A．4.6米 B．4.8米 C．5.米 D．5.2米
5．在△ABC中，
＝5，
＝3，
＝6，则
＝（ ）
A．13 B．26 C．
D．24
6．一个圆锥和一个半球有公共底面，如果圆锥的体积与半球的体积恰好相等，则圆锥轴截面顶角的余弦值是（ ）
A． B．
C．
D．
7．已知双曲线
的离心率
，
．双曲线的两条渐近线构成的角中，以实轴为角平分线的角记为
，则的取值范围是（ ）．
A．
，
B．
，
C．
，
D．
，
8．已知函数
为偶函数
＜＜
，其图像与直线y＝2的某两个交点横坐标为
，
，
的最小值为，则（ ）
A．
，
B．
，
C．，
D．，
9．过抛物线
的焦点作直线l交抛物线于A、B两点，若线段AB中点的横坐标为3，则
等于（ ）
A．10 B．8 C．6 D．4
10．若
，则，，
的大小关系是（ ）
A．
B．
C．
1B．
二、填空题：本题共5小题，共20分，把答案填在题中的横线上
11.若不等式
的解集是非空集合
，m= .
12．
是定义在实数有R上的奇函数，若x≥0时，
，则
________．
13．若点P（
，
）在直线上
上，则
________．
14．用一个与正方体的各面都不平行的平面去截正方体，截得的截面是四边形的图形可能是下列选项中的________（把所有符合条件的图形序号填入）．
①矩形 ②直角梯形
③菱形 ④正方形
15．某宇宙飞船的运行轨道是以地球中心F为焦点的椭圆，测得近地点A距离地面
，远地点B距离地面
，地球半径为
，关于这个椭圆有以下四种说法：
①焦距长为
；②短轴长为
；③离心率
；④若以AB方向为x轴正方向，F为坐标原点，则与F对应的准线方程为
，其中正确的序号为________．
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤．
16.（12分）设函数
的最大值为M,最小正周期为T.
（Ⅰ）求M、T；
（Ⅱ）10个互不相等的正数
满足
求
… +
的值.
17．（12分）无穷数列
的前n项和
，并且
≠
．
（1）求p的值；
（2）求的通项公式；
18．（14分）（甲）如图，已知斜三棱柱
的侧面
⊥底面ABC，∠ABC＝90°，BC＝2，AC＝
，又
⊥，＝．
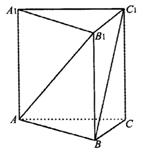
（1）求侧棱
与底面ABC所成的角的大小；
（2）求侧面
与底面所成二面角的大小；
（3）求点C到侧面的距离．
（乙）在棱长为a的正方体
中，E，F分别是棱AB，BC上的动点，且AE＝BF．
（1）求证：
；
（2）当三棱锥
的体积取得最大值时，求二面角
的大小（结果用反三角函数表示）．
19．（14分）在抛物线上存在两个不同的点关于直线l；y＝kx＋3对称，求k的取值范围．
20．（14分）某地区预计明年从年初开始的前x个月内，对某种商品的需求总量（万件）与月份x的近似关系为：
，且
．
（1）写出明年第x个月的需求量
（万件）与月x的函数关系，并求出哪个月份的需求量最大，最大需求量是多少？
（2）如果将该商品每月都投放市场p万件（销售未完的商品都可以在以后各月销售），要保证每月都足量供应，问：p至少为多少万件？
21．（14分）已知函数
的定义域为[
，
]，值域为
，
，并且在
，
上为减函数．
（1）求a的取值范围；
（2）求证：
；
参考答案
1．A 2．B 3．D 4．C 5．B 6．D 7．C 8．A 9．B 10．C
:11. 
12．-1 13．-2 14．①③④ 15．①③④
16. 
……………………2分
（Ⅰ）M=2…………4分 T=
…………6分
（Ⅱ）
…………9分
又
=
………………12分
17．（1）∵ 
∴ 
，且p＝1，或
．
若是，且p＝1，则由
．
∴ 
，矛盾．故不可能是：，且p＝1．由，得
．
又，∴ 
．
（2）∵ 
，
，
∴ 
．
．
当k≥2时，
． ∴ n≥3时有
．
∴ 对一切
有：
．
18．（甲）（1）∵ 侧面
底面ABC， ∴ 在平面ABC上的射影是AC．
与底面ABC所成的角为∠
．
∵ 
，
， ∴ ∠＝45°．
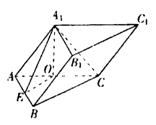
（2）作
⊥AC于O，则⊥平面ABC，再作OE⊥AB于E，连结
，则
，所以∠
就是侧面与底面ABC所成二面角的平面角．
在Rt△中，
，
，
∴ 
． 
60°．
（3）设点C到侧面的距离为x．
∵ 
，
∴ 
．（*）
∵ 
，
， ∴ 
．
又
，∴ 
．
又
． ∴ 由（*）式，得
．∴ 
（乙）（1）证明：如图，以O为原点建立空间直角坐标系．
设AE＝BF＝x，则
（a，0，a），F（a-x，a，0），（0，a，a），E（a，x，0），
∴ 
（-x，a，-a），
（a，x-a，-a）．
∵ 
，
∴ ．
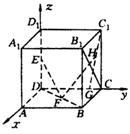
（2）解：记BF＝x，BE＝y，则x＋y＝a，则三棱锥的体积为
．
当且仅当
时，等号成立，因此，三棱锥的体积取得最大值时，
．
过B作BD⊥BF交EF于D，连结
，则
．
∴ ∠
是二面角的平面角．在Rt△BEF中，直角边
，BD是斜边上的高， ∴ 
在Rt△中，tan∠
．故二面角
的大小为
．
19．∵ k＝0不符合题意， ∴ k≠0，作直线
：
，则
．
∴ 满足条件的
由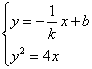
消去x，得
，
．
．（*）
设
，
、
、，则 
．
又
．
∴ 
．
故AB的中点
，
． ∵ l过E， ∴ 
，即 
．
代入（*）式，得
20．（1）
．当x≥2时，
．
∴ 
，且．
∵ 
．
∴ 当x＝12-x，即x＝6时，
（万件）．故6月份该商品的需求量最大，最大需求量为
万件．
（2）依题意，对一切
{1，2，…，12}有
．
∴ 
（x＝1，2，…，12）．
∵ 
∴ 
． 故 p≥1.14．故每个月至少投放1.14万件，可以保证每个月都保证供应．
21．（1）按题意，得
．
∴ 
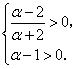即 
．
又
∴ 关于x的方程
．
在（2，＋∞）内有二不等实根x＝、．
关于x的二次方程
在（2，＋∞）内有二异根、．
．
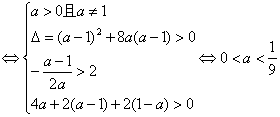故 
．
（2）令
，则
．
∴ ．