高考数学模拟试卷（理） 命题人：株洲市第四中学 陈平方 龚连军
一、 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1、复数
的值是
(
)
A . －1 B．1 C．－32 D．32
2、若{an}是等差数列，则下列结论不正确的是
A.其奇数项a2k-1（k∈N）成等差数列 B.其各项的k倍k an (k是常数)成等差数列
C.各项减去一个常数所得的差an - k (k是常数)成等差数列
D.各项的平方an 2成等差数列
3、
4．直线
与圆
在第一象限内有两个不同的交点，则
的取值范围是
(A) 
(B) 
(C) 
(D) 
5、设
，
，其中O为坐标原点，则
的递增区间是.
A.
, 
B.
,
C.
D.
6、已知平面
平面
，直线
，点
，平面
间的距离为8，则在内到点P的距离为10，且到直线
的距离为9的点的轨迹是（ ）
(A) 一个圆 （B） 四个点 （C） 两条直线 （D） 两个点
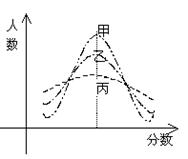7、某次市教学质量检测，甲、乙、丙三科考试 成绩的直方图，如右图所示 (由于人数众多，成绩分 布的直方图可视正态分布)，则由如图曲线可得下列说法中正确的一个是
A.甲科总体的标准差最小
B.丙科总体的平均数最小
C.乙科总体的标准差及平均数都居中
D.甲、乙、丙的总体的平均数不相同
8、过点M(-2，0)的直线m与椭圆交于P1，P2两点，线段P1P2的中点为P,设直线m的斜率为k1(
)，直线OP的斜率为k2，则k1k2的值为 （ ）
（Ａ）2 （Ｂ）－2 （Ｃ）
（Ｄ）－
9、已知 定义域为R的函数满足
，且当x > 2时，单调递增，如果x 1+x 2 < 4 ,且
,则
的值 （ ）
（Ａ）恒小于0 （Ｂ）恒大于0 （Ｃ）可能为0 （Ｄ）可正可负
10、若函数
在其定义域的一个子区间（k-1 , k+1）上不是单调函数，则实数k的取值范围是 （
）
（Ａ）k >
（Ｂ）k
< 
（Ｃ）-
（Ｄ）
二、填空题：本大题共5小题，每小题5分，共25分。把答案填在答题卡中对应题号后的横线上。
11、设 为偶函数，当x > 0时，都有
，又
则
＝
。
12、向量
，若动点P满足条件：
,则p(x,y)的变动范围的面积为
。
13、设
且f(x)中所有项的系数和为A n , 则
。
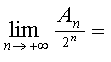14、不等式
对一切
及
都成立，则t的范围是_________
。
15、若
（
为常数，
），则
=_____________ 。
三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.
16、在
中，A,B,C的对边a,b,c,且
,
. （本题12分）
(1)
求的面积s的最大值，
(2) 求a的最小值。
17、某人抛掷一枚质量分布均匀的骰子，出现各数的概率都是
，构造数列
，
|
|
记
(1) 求a 4 = -1时的概率，（2）求s 4= 2 时的概率，
（3）求：前两次均为奇数且s 7 = -1时的概率。（本题12分）
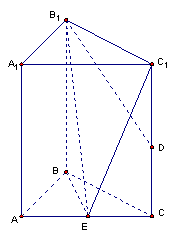18、如图，已知直三棱柱
的侧棱长为４，
是
的中点，
是
棱
上一点．
（１）试确定点的位置,使得
；
（２）若直线
与平面
所成的角为
，
求点Ｄ到平面
的距离．（12分）
19、 据某城市2002年末所做的统计资料显示，到2002年末，该城市堆积的垃圾已达50万吨，侵占了大量的土地，并且成为造成环境污染的因素之一．根据预测，从2003年起该城市还将以每年3万吨的速度产生新的垃圾．垃圾的资源化和回收处理已经成为该市城市建设中的重要问题．
(1)假设1992年底该城市堆积的垃圾为10万吨．从1993年到2002年这十年中，该城市每年产生的新垃圾以8％的年平均增长率增长，试求1993年该城市产生的新垃圾约有多少万吨?(精确到0.01，参考数据：1.08l0≈2.159)
(2)如果从2003年起，该市每年处理上年堆积垃圾的20％，现用b1表示2003年底该市堆积的垃圾数量，b2表示2004年底该市堆积的垃圾数量，……，bn表示2002+n年底该城市堆积的垃圾数量，（i）求b1；（ii）试归纳出bn的表达式(不用证明)；
。（12分）
20、已知点H（0，―3），点P在x轴上，点Q在y轴正半轴上，点M在直线PQ上，且满足
，
.
（1）当点P在x轴上移动时，求动点M的轨迹曲线C的方程；
（2）过定点A（a，b）的直线与曲线C相交于两点S、R，求证：曲线C在S、R两点处的切线的交点B恒在一条直线上.（13分）
21、已知函数是
上每一点处可导的函数，若
在
上恒成立．
（１）求证：函数
在上单调递增；
（２）求证：当
时，有
；
（３）已知不等式
在
且
时恒成立，求证：对一切
有
．（14分）