点与直线 直线方程
一. 教学内容：
点到直线的距离；
点关于点、关于直线的对称点；
直线关于点、关于直线的对称直线；
直线方程复习；
二. 知识点：
1. 点到直线距离公式及证明
关于证明：
根据点斜式，直线PQ的方程为（不妨设A≠0）
解方程组
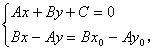
这就是点Q的横坐标，又可得
所以，
。
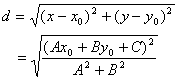
这就推导得到点P（x0，y0）到直线l：Ax+By+C=0的距离公式。
如果A=0或B=0，上式的距离公式仍然成立。
下面再介绍一种直接用两点间距离公式的推导方法。
设点Q的坐标为（x1，y1），则
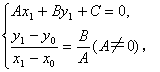
把方程组作变形，
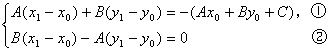
把①，②两边分别平方后相加，得
所以，
所以，
此公式还可以用向量的有关知识推导，介绍如下：
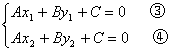
把③、④两式左右两边分别相减，得
由向量的数量积的知识，知
这里n=（A，B）。所以n=（A，B）是与直线l垂直的向量。
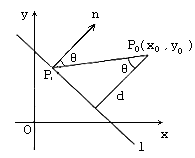
（如图所示）
（如图所示）
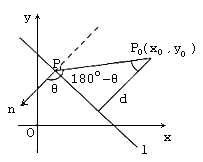
所以，都有
因为
所以
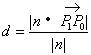
2. 平行线间的距离公式
3. 点关于点的对称点（中点坐标公式）
4. 已知P0（x0，y0）直线l：Ax+By+C=0（B≠0）
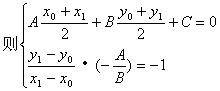
特别地关于特殊直线的对称点。
（x轴、y轴、直线y=x，直线y=－x）
5. 直线l关于点P0（x0，y0）对称直线（三种方法）
6. 
特别地直线l关于特殊直线y=±x+b的对称直线。
【典型例题】
例1. 
解法一：
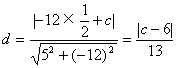
∴c=32或c=－20，
解法二：设所求直线的方程为
由两平行直线间的距离公式，
故所求直线的方程为
小结：求两条平行线之间的距离，可以在其中的一条直线上取一点，求这点到另一条直线的距离，即把两条平行线之间的距离，转化为点到直线的距离。也可以直接套两平行
例2. 已知正方形的中心为G（－1，0），一边所在直线的方程为x+3y－5=0，求其他三边所在的直线方程。
解：正方形中心G（－1，0）到四边距离均为
设正方形与已知直线平行的一边所在直线的方程为x+3y+c1=0。
故与已知边平行的边所在直线的方程为x+3y+7=0
设正方形另一组对边所在直线的方程为3x－y+c2=0。
所以正方形另两边所在直线的方程为：
综上所述，正方形其他三边所在直线的方程分别为：
小结：本例解法抓住正方形的几何性质，利用点到直线的距离公式，求得了正方形其他三边所在直线的方程。
例3. 
解法一：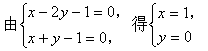
∴点（1，0）为两已知直线的交点。
设所求直线的斜率为k，由一条直线到一条直线的角的公式，
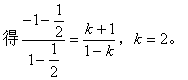
故所求直线方程为
解法二：由解法一知两已知直线的交点为A（1，0）。
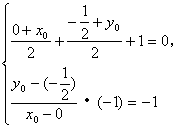
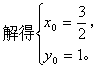
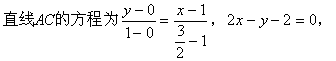
解法三：设P（x，y）是所求直线上的任一点，P关于直线x＋y－1＝0对称的点为P0（x0，y0），
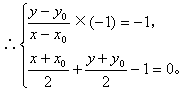
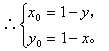
解法四：
直线x+y－1=0 k=－1
由x+y－1=0
代入x－2y－1=0得
1－y－2(1－x)－1=0
2x－y－2=0即为所求。
小结：求直线l关于直线l1对称的直线的方程，只要在l上取两点A、B，求A、B关于l1的对称点A'、B'，然后写出直线A'B'的方程即为所求。解法二和解法三中，都用到了求一个点P关于某直线l的对称点P0的问题。这个问题的解法就是根据：①直线P0P与直线l垂直；②线段P0P的中点在直线l上，列出方程组解出x0、y0，代入x0、y0所满足的方程，整理即得所求直线的方程。
例4. 
截距相等的直线方程。
解法一：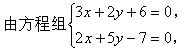
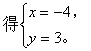
∴两已知直线的交点为（－4，3）。
当所求直线在两坐标轴上的截距都是0时，直线的横截距、纵截距相等。
因为点（－4，3）在直线x+y=a上，
解法二：
小结：解法一设直线的截距式时注意了截距为0的情形。故而没有直接设成
例5. 
列条件的a、b的值。
（1）直线l1过点（－3，－1），并且直线l1与直线l2垂直；
（2）直线l1与直线l2平行，并且坐标原点到l1、l2的距离相等。
分析：考查直线与直线平行及垂直的问题的处理方法。
解：
又点（－3，－1）在l1上，
由①、②解得a=2，b=2。
（2）∵l1∥l2且l2的斜率为1－a。
∴l1的斜率也存在，
故l1和l2的方程可分别表示为
∵原点到l1和l2的距离相等，
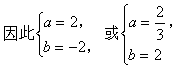
小结：在（2）中由于l1∥l2，l2有斜率，从而得出l1有斜率，即b≠0。
例6. 
最小值时x的值。
解：
它表示点P（x，0）与点A（1，1）的距离加上点P（x，0）与点B（2，2）的距离之和，即在x轴上求一点P（x，0）与点A（1，1）、B（2，2）的距离之和的最小值。
由下图可知，转化为求两点A'（1，－1）和B（2，2）间的距离，其距离为函数f(x)的最小值。
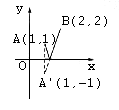
小结：数形结合是解析几何最根本的思想，因此本题联系图形求解，使解法直观、简捷而且准确，易于入手。
例7. 用解析法证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
证明：建立如图所示的坐标系，
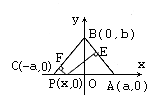
A（a，0），B（0，b），C（－a，0），（a＞0，b＞0），
设底边AC上任意一点为P（x，0）（－a≤x≤a），
∴原命题得证。
例8. 等腰直角三角形斜边所在直线的方程是3x－y＝0，一条直角边所在直线l经过点（4，－2），且此三角形的面积为10，求此直角三角形的直角顶点的坐标。
解：设直角顶点为C，C到直线y=3x的距离为d，
例9. 
（1）求证：不论m为何实数，直线l恒过一定点M；
（2）过定点M作一条直线l1，使l1夹在两坐标轴之间的线段被M点平分，求l1的方程；
（3）若直线l2过点M，且与x轴负半轴、y轴负半轴围成的三角形面积最小，求l2的方程。
解：
它与x轴、y轴分别交于A（a，0），B（0，b）。
∵M为AB中点，由中点坐标公式得a=－2，b=－4，
当且仅当k＝－2时，围成的三角形面积最小，
【模拟试题】
1. 已知直线l经过点P（5，10），且原点到它的距离为5，则直线l的方程为_________。
2. 
，则点P（1，1）到直线
的最大距离是______________。
3. 已知点P（1，
）到直线
，则
_____________。
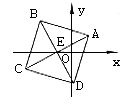
4. 如图，已知正方形ABCD的中心为E（－1，0），一边AB所在的直线方程为
，求其他三边所在直线的方程。
5. 求平行线
的距离。
6. 求过点A（－1，2）且与原点的距离为
的直线方程。
7. 求过点P（1，2）且被两平行直线
截得的线段长为
的直线方程。
8. 求过点P（0，2）且与点A（1，1），B（－3，1）等距离的直线l方程。
9. 原点关于直线
的对称点坐标是（ ）
A. 
B.
C.
D.
（4，3）
（1991年全国高考题）
【试题答案】
1. 
提示：（1）当直线l的斜率存在时，可设l的方程为
。
根据题意，得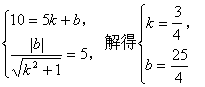
∴所求的直线l的方程为
。
（2）当直线l的斜率不存在时，直线的倾斜角为
，即直线l与x轴垂直。
根据题意，得所求直线l的方程为
。
2. 
提示：点P（1，1）到直线
的距离为
。
∵
最大。
3. 提示：
由
得
，
。
4. 解：可设CD所在直线方程为：
。
∵点E在CD上方，∴m＝－17。经检验不合题意，舍去。
∴m=7，∴CD所在直线方程为
。
∵AB⊥BC，
∴可设BC所在直线方程为
，
则
，∴n=9或－3。
经检验，BC所在直线方程为
AD所在直线方程为
。
综上所述，其他三边所在直线方程为
。
5. 分析：在直线上任取一点，求这点到另一直线的距离。
解：在直线
上任取一点，如P（3，0），
则点P（3，0）到直线
的距离就是两平行线间的距离。
因此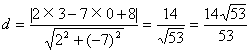
。
［注意］
用上面方法可以证明如下结论：
一般地，两平行直线
和
间的距离为
。
6. 分析：设直线的点斜式方程，利用点到直线的距离公式求出斜率k。
解：设直线方程为
，则
。
∴
，解之得
故所求直线的方程为
或
，
即
。
7. 分析：先画图，由图形易求得两平行直线间的距离为1，则所求直线与两平行直线成45°角，则由夹角公式求得所求直线的斜率
。
解：易求得两平行直线间的距离为1，则所求直线与两平行直线成45°角，
设所求直线的斜率为k，则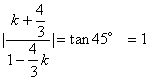
，
解之得。
∴所求直线方程为
。
［注意］
在寻求问题解的过程中，数形结合可优化思维过程。
8. 分析：画图分析，可知符合题意的直线l有2条。
解：画图分析，可知符合题意的直线l有2条。其一直线经过AB的中点；其二直线与AB所在的直线平行。又由AB的中点为（－1，1）得所求直线为
；当所求直线与AB所在的直线平行时，得所求直线方程为
。
9. 解：直线
，与它垂直的直线斜率为
，因此原点关于此直线对称的点应在直线
上。
对照选项，只有（4，3）在直线上，故选D。
［评注］
本题考查直线方程和对称点的有关知识。