高考数学二轮复习直线与圆的位置关系考点透析
【考点聚焦】
考点1：直线的倾角与斜率的概念；
考点2：直线平行与垂直的条件；
考点3：直线与圆的位置关系（特征三角形）。.
【考点小测】
1．（湖南卷）若圆
上至少有三个不同点到直线
:
的距离为
,则直线的倾斜角的取值范围是 ( )
A.[
] B.[
] C.[
D.
解析：圆
整理为
，∴圆心坐标为(2，2)，半径为3
，要求圆上至少有三个不同的点到直线
的距离为
，则圆心到直线的距离应小于等于， ∴ 
，∴ 
，∴ 
，
，
∴ 
，直线的倾斜角的取值范围是
，选B.
2．（江苏卷）圆
的切线方程中有一个是
（A）x－y＝0 （B）x＋y＝0 （C）x＝0 （D）y＝0
【正确解答】直线ax+by=0
，则
，由排除法，
选C,本题也可数形结合，画出他们的图象自然会选C,用图象法解最省事。
【解后反思】直线与圆相切可以有两种方式转化(1)几何条件:圆心到直线的距离等于半径(2)代数条件:直线与圆的方程组成方程组有唯一解,从而转化成判别式等于零来解.
3．（全国卷I）从圆
外一点
向这个圆作两条切线，则两切线夹角的余弦值为
A．
B．
C．
D．
解析：圆的圆心为M(1，1)，半径为1，从外一点
向这个圆作两条切线，则点P到圆心M的距离等于
，每条切线与PM的夹角的正切值等于
，所以两切线夹角的正切值为
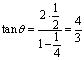，该角的余弦值等于，选B.
5．(重庆卷)过坐标原点且与x2+y2 + 4x+2y+
=0相切的直线的方程为
（A）y=-3x或y=
x (B) y=-3x或y=-x （C）y=3x或y=-x (B) y=3x或y=x
解析：过坐标原点的直线为
，与圆
相切，则圆心(2，－1)到直线方程的距离等于半径
，则
，解得
，∴ 切线方程为
，选A.
6． （辽宁卷）若直线
按向量
平移后与圆
相切，则c的值为（ A ）
A．8或－2 B．6或－4 C．4或－6 D．2或－8
7（北京卷）从原点向圆 x2＋y2－12y＋27=0作两条切线，则该圆夹在两条切线间的劣弧长为 (B )
（A）π （B）2π （C）4π （D）6π
8（湖南卷）设直线
和圆
相交于点A、B，则弦AB的垂直平分线方程是 
.
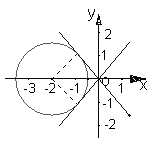9.如果实数满足
,求
的最大值、2x-y的最小值
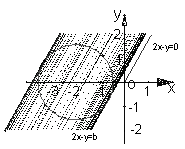解:（1）问题可转化为求圆上一点到原点连线的斜率
的最大值, 由图形性质可知, 由原点向圆作切线,其中切线斜率的最大值即为的最大值
设过原点的直线为y=kx,即kx-y=0,
由
,解得
或
（2）
x,y满足,
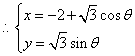
【典型考例】
【问题1】直线的方程与平行、垂直条件
P91 例1
例2.若直线mx+y+2=0与线段AB有交点，其中A(-2, 3)，B(3,2)，求实数m的取值范围。
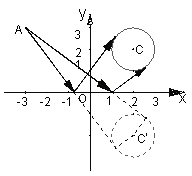例3.自点A(-3,3)发出的光线射到x轴上,被x轴反射,其反射光线所在的直线与圆
相切,求光线所在的直线方程
解:由已知可得圆C：
关于x轴对称的圆C‘的方程为
，其圆心C‘（2，-2），则与圆C’相切，
设: y-3=k(x+3),
，
整理得12k2+
25k+12=0, 解得
或
，
所以所求直线方程为y-3=
(x+3)或 y-3=
(x+3)，
即 3x+4y-3=0或4x+3y+3=0
【问题2】圆的方程
例4.P92 例2
例5.（07年湖南文理科试题）如图，过抛物线x2=4y的对称轴上任一点P（0,m）(m>0)作直线与抛物线交于A,B两点，点Q是点P关于原点的对称点。（I）设点P分有向线段
所成的比为
，证明:
（II）设直线AB的方程是x-2y+12=0，过A,B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程.
解：（Ⅰ）依题意，可设直线AB的方程为 
代入抛物线方程
得
①
设A、B两点的坐标分别是
、
、x2是方程①的两根.
所以 
由点P（0，m）分有向线段
所成的比为，得
又点Q是点P关于原点的对称点，故点Q的坐标是（0，－m），从而
.
所以 
（Ⅱ）由 
得点A、B的坐标分别是（6，9）、（－4，4）.
由 
得 
所以抛物线 在点A处切线的斜率为
设圆C的方程是
则
解之得 
所以圆C的方程是 
即 
例6.一个圆和已知圆
外切,并与直线:
相切于点M（
）,求该圆的方程
已知圆方程化为: 
,其圆心P（1,0）,半径为1
设所求圆的圆心为C（a,b）, 则半径为
,
因为两圆外切,
,从而
1+
(1)
又所求圆与直线：相切于M(),
直线
,于是
,
即 
（2） 将（2）代入（1）化简,得a2-4a=0, a=0或a=4
当a=0时,
,所求圆方程为
当a=4时,b=0,所求圆方程为
【问题3】直线与圆的位置关系
例7.P96T8 例8. P96 T9
【问题3】综合与提高
例9: 例3. 2.(广东卷)在平面直角坐标系中，已知矩形ＡＢＣＤ的长为２，宽为１，ＡＢ、ＡＤ边分别在ｘ轴、ｙ轴的正半轴上，Ａ点与坐标原点重合（如图５所示）．将矩形折叠，使Ａ点落在线段ＤＣ上．
（Ⅰ）若折痕所在直线的斜率为ｋ，试写出折痕所在直线的方程；
（Ⅱ）求折痕的长的最大值．
例10. 23.如图，过圆O：x2+y2=4与y轴正半轴交点A作此圆的切线，M为上任一点，过M作圆O的另一条切线，切点为Q，求△MAQ垂心P的轨迹方程。
【课后训练】
1．（安徽卷）直线
与圆
没有公共点，则
的取值范围是
A．
B．
C．
D．
解：由圆的圆心
到直线大于，且
，选A。
2．(陕西卷)设直线过点(0,a),其斜率为1, 且与圆x2+y2=2相切,则a 的值为( )
A.± B.±2 B.±2 D.±4
解析：设直线过点(0，a)，其斜率为1， 且与圆x2+y2=2相切，设直线方程为
，圆心(0，0)道直线的距离等于半径，∴ 
，∴ a 的值±2，选B．
3．（江西卷） “a=b”是“直线
”的 （A ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分又不必要条件
4 (重庆卷)圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为 (A )
(A) (x-2)2+y2=5； (B) x2+(y-2)2=5； (C) (x+2)2+(y+2)2=5； (D) x2+(y+2)2=5。
5. (全国卷I)已知直线过点
，当直线与圆
有两个交点时，其斜率k的取值范围是（B）
（A）
（B）
（C）
（D）
6．（湖北卷）已知直线
与圆
相切，则的值为
。
解：圆的方程可化为，所以圆心坐标为（1，0），半径为1，由已知可得
，所以
的值为－18或8。
7．（湖北卷）若直线y＝kx＋2与圆(x－2)2＋(y－3)2＝1有两个不同的交点，则k 的取值范围是 .
解：由直线y＝kx＋2与圆(x－2)2＋(y－3)2＝1有两个不同的交点可得直线与圆的位置关系是相交，故圆心到直线的距离小于圆的半径，即
<1，解得kÎ(0，
)
8.(上海卷)已知两条直线
若
，则
____.
解：两条直线若，
，则2.
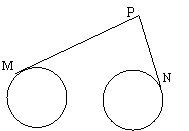9.（江苏卷） 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN（M、N分别为切点），使得
试建立适当的坐标系，并求动点 P的轨迹方程.
解：如图，以直线
为
轴，线段的垂直平分线为
轴，建立平面直角坐标系，则两圆心分别为
．设
，则
，同理
．
∵
，
∴
，
即
，即
．这就是动点
的轨迹方程．
10、当0<a<2时，直线L1：ax-2y-2a+4=0与L2：2x+a2y-2a2-4=0和坐标轴成一个四边形，要使围成的四边形面积最小，a应取何值？
11．已知圆C: x2+y2-2x+4y-4=0,是否存在斜率为1的直线L,使以L被圆C截得弦AB为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由
解:设直线L的斜率为１，且L的方程为y=x+b,则
消元得方程２x2+（2b+2）x+b2+4b-4=0,设此方程两根为x1,x2，则x1＋x2＝－（b+1）,y1+y2= x1＋x2+2b=b-1,则ＡＢ中点为
，又弦长为
＝
，由题意可列式
＝
解得b=1或b=-9,经检验b=-9不合题意．所以所求直线方程为y=x+1
考点透析10答案:
考点小测答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | C | B | A | A | B | 3x-2y-3=0 |
|
课后练习答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | A | A | B | －18或8 | (0， | 2 | (X-6)2+Y2=33 |
|