七、直线与圆的方程
考试要求：1、理解直线的倾斜角和斜率的概念，掌握过两点的直线的斜率公式。掌握直线方程的点斜式、两点式、一般式，并能根据条件熟练地求出直线方程。2、掌握两条直线平行与垂直的条件，两条直线所成的角和点到直线的距离公式。能够根据直线的方程判断两条直线的位置关系。3、了解二元一次不等式表示平面区域。4、了解线性规划的意义，并会简单地应用。5、了解解析几何的基本思想，了解坐标法。6、掌握圆的标准方程和一般方程，了解参数方程的概念，理解圆的参数方程。
1、与直线
垂直的直线的倾斜角为:
A．
B．
C．
D．
2、过坐标原点且与点（
）的距离都等于1的两条直线的夹角为：
A．90° B．45° C．30° D．60°
3、直线
的方程为
，直线
与直线关于直线
对称，则直线经过点
A．（－1，3） B．（1，－3） C．（3，－1） D．（－3，1）
4、直线
平行，则a等于：
A．
B．2 C．－1 D．2或－1
5、已知x、y满足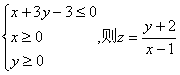
的取值范围是：
A．[－2，1] B．
C．[－1，2]D．
6、设x，y满足约束条件：
的最大值与最小值分别为：
A．
，3 B．5， C．5，3 D．4，3
7、若
，则
的最小值为：
A．
B．
C．
D．
8、已知圆的方程为x2 – 2x + y2 – 4y – 5 = 0，则圆心坐标为_________，圆与直线y = 5相交所得的弦长为_____________．
9、设
，则直线
与圆
的位置关系是:
A. 相切 B. 相交 C. 相切、相离或相交 D. 相交或相切
10、若直线
和圆
切于点
，则ab的值为：
A. 2 B. 
C. 
D.
3
11、若直线
被圆
截得的弦长为4，
则
的最小值是
A.2
B.4
C.
D.
12．过原点向圆x
+y－6y+
=0作两条切线, 则两条切线间圆的劣弧长为：
A. 
B.
C.
D.
13、已知直线
不全为0）与圆
有公共点，且公共点的横、纵坐标均为整数，那么这样的直线共有
A．66条 B．72条 C．74条 D．78条
14、若点P在曲线
上移动，经过点P的切线的倾斜角为
，
则角的取值范围是：
A．
B．
C．
D．
|
上一动点，把纸片折叠使M与F重合，然后抹平纸片，折
痕为CD，设CD与OM交于P，则点P的轨迹是：
A．椭圆 B．双曲线
C．抛物线 D．圆
16、与两圆
都外切的动圆的圆心在：
A．一个椭圆上 B．双曲线的一支上
C．椭圆的一部分上 D．双曲线上
17、若点
满足等式
，则点P的轨迹是：
A．圆 B．椭圆 C．双曲线 D．抛物线
18、圆C：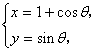
（
为参数）的普通方程为__________，设O为坐标原点，点M（
）在C上运动，点P（x，y）是线段OM的中点，则点P的轨迹方程为____。
19、过点C（6，－8）作圆
的切线于切点A、B，那么C到直线AB的距离为：
A．15 B．
C．5 D．10
20、已知圆(x－3)2+y2=4和直线y=mx的交点分别为P，Q两点，O为坐标原点，则
的值为
。
21、过椭圆
上的动点P引圆
的两条切线PA、PB，切点分别为A、B，直线AB与
轴、
轴分别交于点M、N.
（Ⅰ）设P点坐标为
，求直线AB的方程；
（Ⅱ）求△MON面积的最小值（O为坐标原点）.
七、直线与圆的方程参考答案
1、B；2、D；3、C；4、D；5、B；6、C；7、C；8、
；10、A；11、B；14、B；
15、A；16、B；17、D；18、
,
；19、B；20、5
21．解：（I）设A（
），B（
），则直线PA的方程为
，
直线PB的方程为
又P（
在PA、PB上，所以，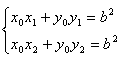
故A、B两点的坐标满足
，∴直线AB的方程为
（Ⅱ）在
中，令
得
即M（
，0），N（0，
）
∴S△MON=
∴S△MON=
当且仅当
时，S△MON取最小值