直线、平面、简单几何体综合训练
一. 教学内容:
直线、平面、简单几何体综合训练
【模拟试题】
第I卷(选择题 共60分)
一. 选择题:
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 室内有一根直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在的直线( )
A. 异面 B. 相交 C. 平行 D. 垂直
2. 正三棱锥相邻两侧面所成的角为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() )
)
C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
3. 已知二面角![]() 的大小为
的大小为![]() ,
,![]() 和
和![]() 是两条异面直线,则在下列四个条件中,不能使
是两条异面直线,则在下列四个条件中,不能使![]() 和
和![]() 所成的角为
所成的角为![]() 的是( )
的是( )
A. ![]() ,
,![]() B.
B.
![]() ,
,![]()
C. ![]() ,
,![]() D.
D.
![]() ,
,![]()
4. 已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() 的一个必要不充分条件是( )
的一个必要不充分条件是( )
A. ![]() ,
,![]() B.
B.
![]() ,
,![]()
C. ![]() ,
,![]() D.
D.
![]() 、
、![]() 与
与![]() 成等角
成等角
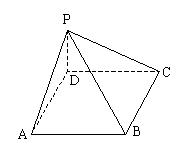
5. 如图,ABCD为正方形,点P为平面AC外一点,PD⊥平面ABCD,PD=AD=![]() ,设点C到平面PAB的距离为
,设点C到平面PAB的距离为![]() ,点B到平面PAC的距离为
,点B到平面PAC的距离为![]() ,则有( )
,则有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 把正方形ABCD沿对角线BD折成直二面角,对于下列结论:
① AC⊥BD;② ![]() 是正三角形;③ AB与CD成
是正三角形;③ AB与CD成![]() 角;④ AB与平面BCD成
角;④ AB与平面BCD成![]() 角。则其中正确结论的个数是( )
角。则其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
7. 若3个平面将空间分成![]() 部分,则
部分,则![]() 的值为( )
的值为( )
A. 4 B. 4或6 C. 4或6或7 D. 4或6或7或8
8. 正三棱锥![]() 的三条侧棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为( )
的三条侧棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 设地球表面积为S,则地球表面上从A地(北纬![]() ,东经
,东经![]() )到B地(北纬
)到B地(北纬![]() ,东经
,东经![]() )的最短距离为( )
)的最短距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 设球O的半径为R,A,B,C为球面上三点,A与B、A与C的球面距离都为![]() R,B与C的球面距离为
R,B与C的球面距离为![]() ,则球O在二面角
,则球O在二面角![]() 内的那一部分的体积是( )
内的那一部分的体积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
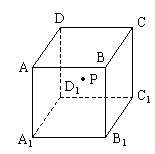
11. 如下图,在正方体![]() 的侧面
的侧面![]() 内有一点P到直线
内有一点P到直线![]() 与到直线
与到直线![]() 的距离相等,则动点P所在曲线的大致形状是( )
的距离相等,则动点P所在曲线的大致形状是( )
A. 一条线段 B. 一段椭圆弧 C. 一段抛物线 D. 一段圆弧
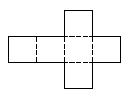
12. 如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形后,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
第II卷(非选择题 共90分)
13. 在正方体![]() 中,E、F分别是
中,E、F分别是![]() 、DC的中点,直线
、DC的中点,直线![]() 与平面ADE所成的角是 。
与平面ADE所成的角是 。
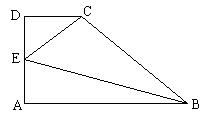
14. 一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,BC=![]() ,CD=1,E为AD中点,沿CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的体积等于 。
,CD=1,E为AD中点,沿CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的体积等于 。

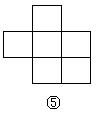
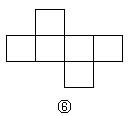
15. 如下图,在下列六个图形中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是 (要求:把你认为正确图形的序号都填上)。
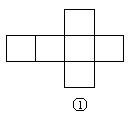
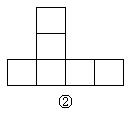
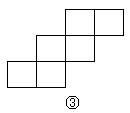
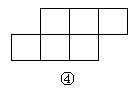
16. 已知![]() 、
、![]() 是两个不同的平面,
是两个不同的平面,![]() ,
,![]() 是平面
是平面![]() 及
及![]() 之外的两条不同直线,给出四个论断:①
之外的两条不同直线,给出四个论断:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() 。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。
。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。
三. 解答题:
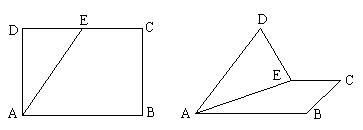
17. 在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将![]() 折起,使二面角
折起,使二面角![]() 为
为![]() 。
。
(1)求DE与平面AC 所成角的大小
(2)求二面角![]() 的大小
的大小
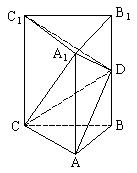
18. 如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,D为棱
,D为棱![]() 的中点。
的中点。
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求证:平面![]() 平面ADC
平面ADC
19. 已知S是![]() 所在平面外一点,O是边AC的中点,
所在平面外一点,O是边AC的中点,![]() ,点P是SA的中点。
,点P是SA的中点。
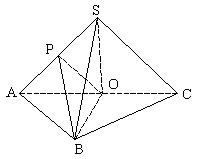
(1)求证:![]() 平面ABC
平面ABC
(2)求证:![]() 平面BOP
平面BOP
(3)若![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,又SC与平面BOP的距离为
,又SC与平面BOP的距离为![]() ,求二面角
,求二面角![]() 的大小。
的大小。
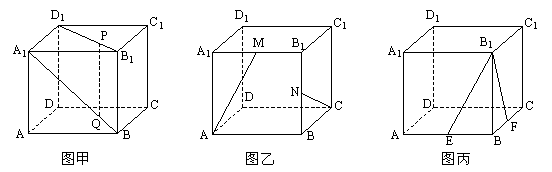
20. 在棱长为1的正方体![]() 中
中
(1)P、Q分别是![]() 、
、![]() 上的点且
上的点且![]() ,
,![]() (如图甲)。求证:PQ//平面
(如图甲)。求证:PQ//平面![]()
(2)M、N分别是![]() 、
、![]() 的中点(如图乙),求直线AM与CN所成的角
的中点(如图乙),求直线AM与CN所成的角
(3)E、F分别是AB、BC的中点(如图丙),试问在棱![]() 上能否找到一点H,使
上能否找到一点H,使![]() 平面
平面![]() ?若能,试确定点H的位置,若不能,请说明理由。
?若能,试确定点H的位置,若不能,请说明理由。
【试题答案】
一.
1—6 DDCDDC 7—12 DDCBCB
二.
13.
![]() 14.
14. ![]() 15. ①③⑥ 16. ②③④
15. ①③⑥ 16. ②③④![]() ①或①③④
①或①③④![]() ②
②
三.
17.
如图甲所示,过点D作DM⊥AE于M,延长DM与BC交于N,在翻折过程中DM⊥AE,MN⊥AE保持不变,翻折后,如图乙,![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,AE⊥平面DMN,又因为
,AE⊥平面DMN,又因为![]() 平面
平面![]() ,则平面
,则平面![]() 平面DMN
平面DMN
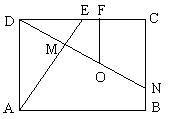
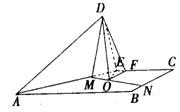
图甲 图乙
(1)在平面DMN内,作DO⊥MN于O
∵ 平面AC⊥平面DNM ∴ DO⊥平面AC
连结OE,DO⊥OE,![]() 为DE与平面AC所成的角
为DE与平面AC所成的角
如图甲,在直角三角形ADE中,AD=3,DE=2
![]()
![]() ,
,![]()
如图乙,在直角三角形DOM中,![]() ,
,
在直角三角形DOE中,![]()
则![]() ∴ DE与平面AC所成的角为
∴ DE与平面AC所成的角为![]()
(2)如图乙,在平面AC内,作OF⊥EC于F,连结DF
∵ DO⊥平面AC ∴ DF⊥EC ∴ ![]() 为二面角
为二面角![]() 的平面角
的平面角
如图甲,作![]() 于F,则
于F,则![]() ∽
∽![]()
![]() ∴
∴ ![]()
如图乙,在![]() 中,
中,![]()
如图甲,![]() ,
,![]()
在![]() 中,
中,![]()
∴ 二面角![]() 的大小为
的大小为![]()
18. 解法一:
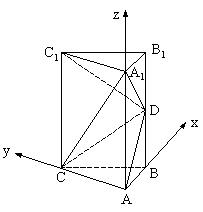
(1)建立如下图所示的平面直角坐标系。
设![]() ,则
,则![]() (0,0,
(0,0,![]() ),C(0,
),C(0,![]() ,0),C1(0,
,0),C1(0,![]() ,
,![]() ),D(
),D(![]() ,0,
,0,![]() ),于是
),于是![]() ,
,![]() 。
。
∵ 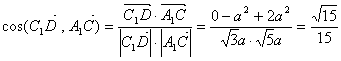
∴ 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
(2)∵ ![]() ,
,![]() ,
,![]()
∴ ![]() ,
,![]()
则![]() ,
,![]() ∴
∴ ![]() ⊥平面ADC,又
⊥平面ADC,又![]() 平面
平面![]()
∴ 平面![]() 平面
平面![]()
解法二
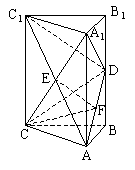
(1)连结![]() 交
交![]() 于点E,取AD中点F,连结EF,则EF∥C1D
于点E,取AD中点F,连结EF,则EF∥C1D
∴ 直线EF与A1C所成的角就是异面直线![]() 与
与![]() 所成的角
所成的角
设![]() 则
则![]()
![]()
![]()
![]() 中,
中,![]()
![]()
直三棱柱中,![]() 面ABC,
面ABC,![]() ,则
,则![]()
![]()
∵ ![]()
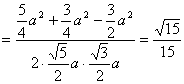
∴ 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
(2)直三棱柱中,![]() ∴
∴ ![]() 平面
平面![]() ,则
,则![]()
又 ![]() ,
,![]() ,
,![]() ,则
,则![]() ,于是
,于是![]()
∴ ![]() 平面
平面![]() ,又
,又 ![]() 平面
平面![]()
∴ 平面![]() 平面ADC
平面ADC
19.
(1)在平面![]() 中,
中,![]() 又
又 ![]()
∴ ![]() 即
即![]() ,
,![]()
∴ ![]() 平面ABC
平面ABC
(2)∵ P是SA的中点,O是AC的中点 ∴ OP∥SC 而![]() 平面BOP
平面BOP
![]() 平面BOP ∴ SC∥平面BOP
平面BOP ∴ SC∥平面BOP
(3)由SO⊥平面ABC知平面SAC⊥平面ABC
又等腰直角![]() 中,BO⊥AC,∴ BO⊥平面SAC
中,BO⊥AC,∴ BO⊥平面SAC
在![]() 中,作OM⊥SC于M,连BM,则BM⊥SC
中,作OM⊥SC于M,连BM,则BM⊥SC
∴ ![]() 为二面角
为二面角![]() 的平面角
的平面角
由![]() ,OM⊥OB知,OM⊥平面BOP
,OM⊥OB知,OM⊥平面BOP
∴ OM是SC与平面BOP的距离,![]()
又 ![]()
在![]() 中,
中,![]() ∴
∴ ![]()
即二面角![]() 的大小为
的大小为![]() 。
。
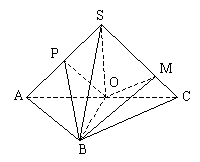
20.
(1)证法一:在![]() 上取点
上取点![]() ,
,![]() 上取点Q,使
上取点Q,使![]()
![]() ,由已 知得
,由已 知得![]()
∴ ![]() 且
且![]()
在平面AA1B1B中同理可证1∥AB,且![]()
∴ ![]() ∴ PQ∥P1Q1
又
∴ PQ∥P1Q1
又 ![]() 平面
平面![]()
∴ ![]() //平面AA1D1D
//平面AA1D1D
证法二:
以D为原点,建立空间直角坐标系,使下列各点的坐标为D1(0,0,1),B1(1,1,1),A1(1,0,1),B(1,1,0),又已知P(![]() ,
,![]() ,1),Q(1,
,1),Q(1,![]() ,
,![]() ),在
),在![]() 、
、![]() 上取点P1、Q1,使满足
上取点P1、Q1,使满足![]() ,
,![]() ,则由定比分点公式得
,则由定比分点公式得![]() ,
,![]() ,∴
,∴ ![]() ,
,![]()
∴ ![]() ∴ PQ//平面AA1D1D
∴ PQ//平面AA1D1D
(2)解法一:
取AB中点![]() ,CC1中点
,CC1中点![]() 连
连![]() 、
、![]() 、
、![]() ,则
,则![]() ,
,![]()
∴ ![]() 即为AM与CN所成的角
即为AM与CN所成的角
在![]() 中,
中,![]()
![]() ,由余弦定理得
,由余弦定理得![]()
∴ AM与CN所成的角为![]() 。
。
解法二:
以D为原点建立空间直角坐标系,使下列各点坐标为A(1,0,0),M(1,![]() ,1),N(1,1,
,1),N(1,1,![]() ),C(0,1,0)
),C(0,1,0)
∴ ![]() ,
,![]()
∴ 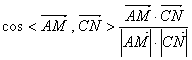
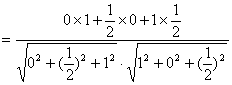
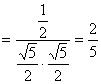
∴ AM与CN所成的角为![]()
(3)解法一:
能找到点H。∵ ![]() ∴ BH在底面的射影为BD,则BH⊥EF恒成立,若BH⊥平面BEF,则HB⊥B1F必成立。设H在BB1C1C内射影为H1,
∴ BH在底面的射影为BD,则BH⊥EF恒成立,若BH⊥平面BEF,则HB⊥B1F必成立。设H在BB1C1C内射影为H1,![]() 必成立。
必成立。
易证![]() ,∴
,∴ ![]() ,即H1是CC1中点。
,即H1是CC1中点。
∴ H也必是DD1中点,∴ 这样的点存在且是DD1之中点。
解法二:
以D为原点建立空间直角坐标系,设H坐标为(0,0,![]() ),B1(1,1,0),B(1,1,0),F(
),B1(1,1,0),B(1,1,0),F(![]() ,1,0),BH⊥EF恒成立(如解法一)
,1,0),BH⊥EF恒成立(如解法一)
若BH⊥平面B1EF,则BH⊥B1F。即![]()
又![]() ,
,![]()
∴ ![]() 即
即![]()
∴ ![]() ,故存在点H是DD1之中点
,故存在点H是DD1之中点