直线方程及其应用
一. 教学内容:
直线方程及其应用
【教学要求】
1. 理解直线斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练求出直线方程。
2. 掌握两直线平行、垂直的条件;掌握两条直线所成角的公式和点到直线的距离公式。
3. 了解二元一次不等式表示平面区域,了解线性规划的意义,并会简单应用。
二. 知识串讲:
(一)基本公式
1. 有向线段
设P1(x1,y1),P2(x2,y2)
![]()
![]()
![]()
![]()
![]()
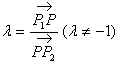

P为内分点,λ>0;P为外分点,λ<0。
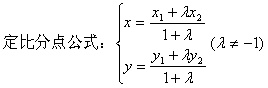
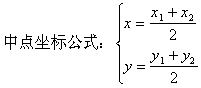
例如:设△ABC,A(x1,y1),B(x2,y2),C(x3,y3)
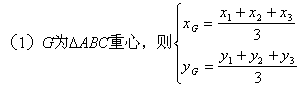
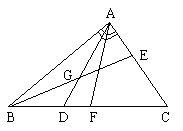
![]()
2. 直线l的倾斜角α(直线向上的方向与x轴的正方向所成的最小正角)
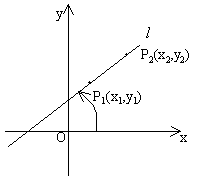
![]()
![]()
![]()
![]()
![]()
(二)直线方程
1. 直线方程:
(1)点斜式:
y-y0=k(x-x0)(已知:点P0(x0,y0),斜率k)
(2)斜截式:
y=kx+b(已知:斜率k及纵截距b)
(3)两点式:
![]()
(4)截距式:
![]()
(5)一般式:
Ax+By+C=0(A、B不同时为0)
2. 两条直线的位置关系:
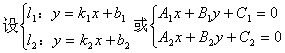
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(5)夹角θ:按逆时针方向从l1转到l2所成的角,叫做l1到l2的角。
![]()
两条直线相交所成的锐角或直角,叫做两条直线的夹角θ。
![]()
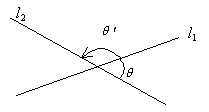
![]()
![]()
![]()
3. 点到直线的距离公式:
P(x0,y0)是已知点,l:Ax+By+C=0是已知直线,则
![]()
4. 对称点:
![]()

5. 直线系方程:
(1)过定点(x1,y1)的直线系方程:
![]()
(2)平行于直线Ax+By+C=0的直线系方程:
![]()
(3)垂直于直线Ax+By+C=0的直线系方程:
![]()
![]()
系方程:
![]()
(三)简单的线性规划
1. 二元一次不等式表示平面区域
一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
只需在此直线的某一侧取一特殊点(x0,y0)从Ax0+By0+C的正、负即可判断Ax+By+C>0表示直线哪一侧的区域。(若C≠0时,可取原点(0,0))

![]()
由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分。
2. 线性规划:
I. 基本概念:
(1)线性约束条件:
由x,y的一次不等式(或方程)组成的不等式组,是对x,y的约束条件。
(2)目标函数:
![]()
线性目标函数:关于x,y的一次解析式。
(3)可行解:满足线性约束条件的解(x,y)。
(4)可行域:所有可行解组成的集合。
(5)最优解:使目标函数达到最值的可行解。
(6)线性规划问题:求线性目标函数在约束条件下的最大(小)值问题。
II. 用图解法解线性规划的步骤:
(1)分析并将已知数据列出表格;
(2)确定约束条件;
(3)确定线性目标函数;
(4)画出可行域;
(5)利用线性目标函数,求出最优解;
(6)实际问题需要整数解时,应适当调整确定最优解。
例如:已知动点(x,y)所在区域是如图所示的阴影部分(包括边界),则目标函数z=x+2y的最小值和最大值分别为_____________。

解:作直线x+2y=0
平移此直线经过第一个点是(1,0)
![]()
再往上平移到最后一点为(4,4)
![]()
【典型例题】
例1. ![]()
![]()
![]()
解析:![]()
![]()
![]()
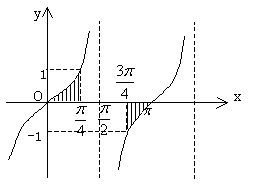
![]()
![]()
∴选C
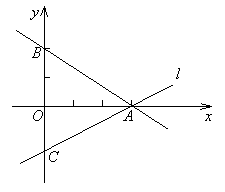
例2. ![]()
![]()
解析1:求出交点坐标,再由交点在第一象限求得斜率的范围,进而得到倾斜角的范围。
解析2:![]()
![]()
![]()
![]()
![]()
![]()
例3. 一条直线经过点P(2,3),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍。
(2)与x,y轴的正半轴交于A、B两点,且△AOB的面积最小。
解:(1)设所求直线的倾斜角为θ,已知直线的倾斜角为α,则
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
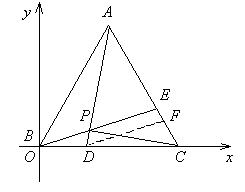
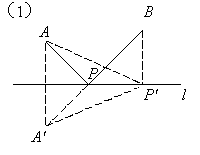
例4. ![]()
![]()
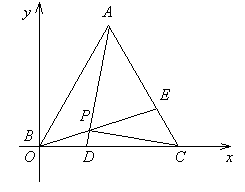
证明一:以B为坐标原点,直线BC为x轴,建立如图所示的直角坐标系。
取BC为单位长1,则各点坐标为:
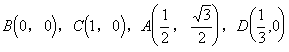
![]()
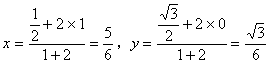
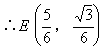
![]()
![]()
![]()
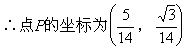
![]()
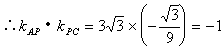
∴AP⊥CP
证明二:以B为坐标原点,直线BC为x轴,建立如图所示的直角坐标系,过D作DF∥BE交AC于F点,取BC为单位长1,则
![]()
![]()
![]()

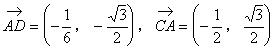
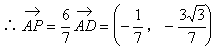
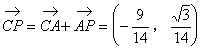
![]()
∴AP⊥CP
说明:数形结合强调的是将代数问题几何化,而解析法则是通过坐标系将几何问题代数化。
例5. 已知直线l1:mx+8y+n=0与l2:2x+my-1=0互相平行,求过点
![]()
解:![]()
![]()
![]()
![]()
![]()
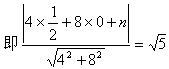
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
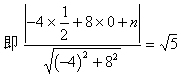
![]()
![]()
![]()
![]()
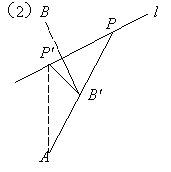
例6. ![]()
解:![]()
解法1:在直线l1上取一点B(2,0),设点B关于直线l的对称点C的坐标为C(x0,y0)
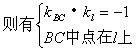
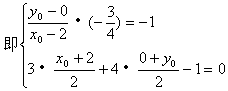
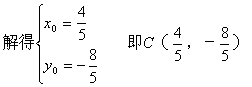
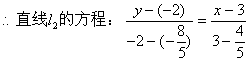
![]()
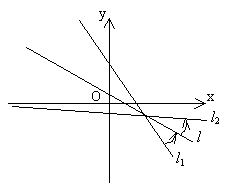
解法2:![]()
到角公式):
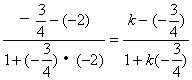
![]()
![]()
![]()
例7. ![]()
![]()
![]()
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
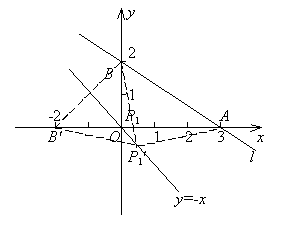
![]()
![]()
![]()
(由三角形两边之差小于第三边)
![]()
![]()
且为1。
![]()
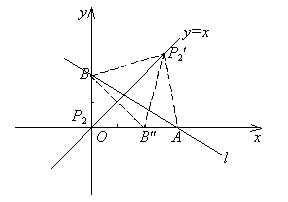
注:
![]()
![]()
![]()
例8. ![]()
A. 只能是(-3,0)
B. 只能是(0,6)
C. 只能是(-3,0)或(0,6)
D. 有无数个
解析:![]()
则平移向量为(-3,0),就可能误选A。
![]()
![]()
![]()
![]()
![]()
显然(h,k)不唯一确定
∴选D
例9. 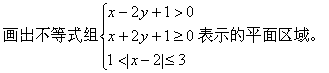
解:![]()
![]()
![]()
![]()
带状区域,但不包括直线x=1和x=3上的点。
所以,原不等式组表示的区域如图所示:

例10. 某工厂有甲、乙两种产品,计划每天各生产量不少于15t,已知生产甲产品1t,需煤9t,电力4kW·h,劳动力3个;生产乙产品1t需煤4t,电力5kW·h,劳动力10个。甲产品每1t利润7万元,乙产品每1t利润12万元,但每天用煤不超过300t,电力不超过200kW·h,劳动力只有300个,问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
分析:将已知数据列成表:

解:设每天生产甲、乙两种产品分别为x t,y t,利润总额为z万元
![]()
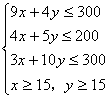
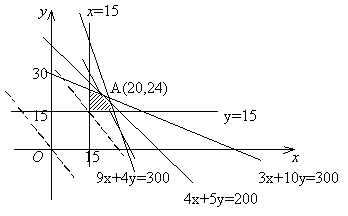
如图作出可行域,作出一组平行直线7x+12y=m(m为参数)中,经过可行域内的点且和原点距离最远的直线,此直线过4x+5y=200和3x+10y=300的交点A(20,24),即生产甲、乙两种产品分别为20t、24t时,利润总额最大,
![]()
【模拟试题】
一. 选择题。
1. 直线![]() 经过二、三、四象限,
经过二、三、四象限,![]() 的倾斜角为
的倾斜角为![]() ,斜率为k,则( )
,斜率为k,则( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
2. 经过点(10,![]() )且倾斜角的余弦值为
)且倾斜角的余弦值为![]() 的直线方程是( )
的直线方程是( )
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
3. 直线![]() 过点P(1,2)且与两坐标轴围成等腰三角形,则
过点P(1,2)且与两坐标轴围成等腰三角形,则![]() 的方程为( )
的方程为( )
A. ![]() B.
B.
![]() 或
或![]()
C. ![]() D.
D.
![]() 或
或![]()
4. 已知两条直线![]() ,其中a为实数,当这两条直线的夹角在
,其中a为实数,当这两条直线的夹角在![]() 内变动时,a的取值范围是( )
内变动时,a的取值范围是( )
A.
![]() B.
B.
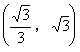
C.
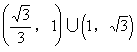 D.
D. ![]()
5. 点A(4,5)关于直线![]() 的对称点为
的对称点为![]() ,则
,则![]() 的方程为( )
的方程为( )
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
6. 在约束条件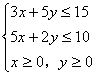 下,目标函数
下,目标函数![]() ( )
( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二. 填空题。
7. 从M(2,2)射出一条光线,经过x轴反射后过点N(![]() ,3),则反射点P的坐标为__________。
,3),则反射点P的坐标为__________。
8. 已知过点![]() 及Q(0,b)的直线的倾斜角介于120°与150°之间,则b的取值范围是______________。
及Q(0,b)的直线的倾斜角介于120°与150°之间,则b的取值范围是______________。
9. 如果直线![]() 与直线
与直线![]() 平行,那么系数a等于__________。
平行,那么系数a等于__________。
10. 如果直线![]() 与直线
与直线![]() 互相垂直,那么a的值为________。
互相垂直,那么a的值为________。
11. 直线![]() 过点(2,1),且原点到
过点(2,1),且原点到![]() 的距离是1,则
的距离是1,则![]() 的方程是________________。
的方程是________________。
三. 解答题。
12. 如图,已知△ABC的三边方程分别为![]() ,BC:
,BC:![]() ,CA:
,CA:![]() ,求:
,求:
(1)∠B的大小;
(2)∠BAC的内角平分线所在直线的方程;
(3)AB边上的高所在直线的方程。
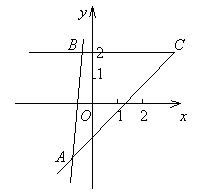
13. 若一直线被直线![]() 和
和![]() 截得的线段的中点恰好在坐标原点,求这条直线的方程。
截得的线段的中点恰好在坐标原点,求这条直线的方程。
14. 预算用2000元购买单价为50元的桌子和20元的椅子,希望使桌子、椅子的总数尽可能的多,但椅子数不少于桌子数,且不多于桌子数的1.5倍,问桌、椅各买多少才行。
【试题答案】
一. 选择题。
1. B 2. A 3. B
4. C
提示:直线![]() 的倾斜角为
的倾斜角为![]()
依题意![]() 的倾斜角的取值范围为
的倾斜角的取值范围为 ![]()
即![]()
从而![]() 的斜率
的斜率![]() 的取值范围为
的取值范围为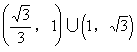
答:选C。
5. B 6. C
二. 填空题。
7. ![]()
8. ![]()
提示:![]()
![]()
9. ![]()
10. ![]()
11. ![]() 或
或![]()
三. 解答题。
12. 解:(1)由已知得:![]()
∠B是直线BA到BC的角
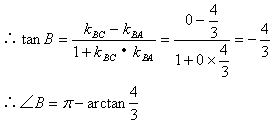
(2)设![]() 为∠BAC平分线上任意一点,则
为∠BAC平分线上任意一点,则
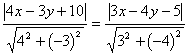
解得:![]() 或
或![]()
(一条为∠BAC内角平分线,另一条为外角平分线)
由图形知![]() 即为所求。
即为所求。
(3)先求出BC与AC的交点![]() ,
,![]()
∴AB边上的高线的斜率为![]()
![]() ,即
,即![]()
13. 由于两已知直线在y轴上的截距不是互为相反数,故所求直线不是y轴,设所求直线方程为![]() ,由
,由![]() 得交点为
得交点为![]()
因为A点关于原点对称点![]() 在直线
在直线![]() 上
上
代入,得![]()
故所求直线的方程为![]()
14. 解:设桌、椅分别买x、y张,把所给的条件表示成x,y的不等式组为
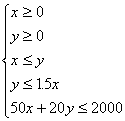
设目标函数a=x+y作出可行域,如图:

![]()
![]()
可行性区域为△AOB(包括边界)
由a=x+y,得![]() ,表示斜率为
,表示斜率为![]() ,y轴上的截距为a的平行直线系,要使a最大,如图只有直线系过B点。
,y轴上的截距为a的平行直线系,要使a最大,如图只有直线系过B点。
![]()
由于y取整数,故取y=37
∴买桌子25张,椅子37把是最优选择。