高考数学概率与统计变式题

高考数学复习概率与统计变式题（命题人：广州市第三中学 刘窗洲）

　　　　　　　　　　　　　　　　　　　　　　　  审校人　张志红

1．（人教A版选修2-3第66页例4）

某射手每次射击击中目标的概率是 ，求这名射手在 10 次射击中，

（1）恰有 8 次击中目标的概率；

（2）至少有 8 次击中目标的概率 ？

变式1：某人参加一次考试，４道题中解对３道则为及格，已知他的解题正确率为，则他能及格的概率为　　　　　　  ．

【解析】：他能及格则要解对４道题中解对３道或４道：解对３道的概率为：，解对4道的概率为：，且A与B互斥，他能及格的概率为．

变式2：设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。

（1）　　　 三人各向目标射击一次，求至少有一人命中目标的概率及恰有两人命中目标的概率；

　　　（2） 若甲单独向目标射击三次，求他恰好命中两次的概率．

　　　　　　　　　　　【解析】（I）设A_K表示“第k人命中目标”，k=1，2，3.

　　　 这里，A₁，A₂，A₃独立，且P（A₁）=0.7，P（A₂）=0.6，P（A₃）=0.5.

　 　　　 从而，至少有一人命中目标的概率为

　 　　　

　　　 恰有两人命中目标的概率为

　　　

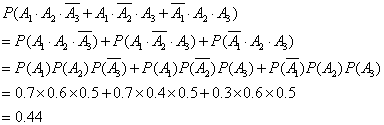
　 　　　 答：至少有一人命中目标的概率为0.94，恰有两人命中目标的概率为0.44．

（II）设甲每次射击为一次试验，从而该问题构成三次重复独立试验.又已知在每次试验中事件“命中目标”发生的概率为0.7，故所求概率为

　　　　　　　　　　　

　　　答：他恰好命中两次的概率为0.441.

变式3：在2004年雅典奥运会中，中国女排与俄罗斯女排以“五局三胜”制进行决赛，根据以往战况，中国女排在每一局赢的概率为　 已知比赛中，俄罗斯女排先胜了每一局，求：

(1)  中国女排在这种情况下取胜的概率；

(2)  求本场比赛只打四局就结束的概率．（均用分数作答）

【解析】(1)中国女排取胜的情况有两种，第一种是中国女排连胜三局，第二种是在第2局到第4局，中国女排赢了两局，第5局中国女排赢，∴中国女排取胜的概率为

(2)

变式4： 一个质地不均匀的硬币抛掷5次,正面向上恰为1次的可能性不为0,而且与正面向上恰为2次的概率相同.令既约分数为硬币在5次抛掷中有3次正面向上的概率,求.

【解析】设正面向上的概率为P,依题意:

,1-P=2P,

解得:,

硬币在5次抛掷中有3次正面向上的概率为:

.

2．（人教A版选修2-3第77页例4）

随机抛掷一枚质地均匀的骰子，求向上一面的点数的均值、方差和标准差。

变式1：设某射手每次射击打中目标的概率为，现在连续射击４次，求击中目标的次数ξ的概率分布．

【解析】击中目标的次数ξ可能为0，1，2，3，4。

当ξ=0时，，

当ξ=1时，，

当ξ=2时，，

当ξ=3时，，

当ξ=4时，，

所以ξ的分布列为：

ξ	0	1	2	3	4
P

变式2：袋中有１２个大小规格相同的球，其中含有２个红球，从中任取３个球，求取出的３个球中红球个数ξ的概率分布．

【解析】ξ的所有可能的取值为：0，1，2．

当ξ=0时，，

当ξ=1时，，

当ξ=2时，，

ξ	0	1	2
P

评述：++==1．

变式3：从4名男生和2名女生中任选3人参加演讲比赛，设随机变量表示所选3人中女生的人数.

  （1）求的分布列；

（2）求的数学期望；

（3）求“所选3人中女生人数”的概率.

【解析】（1）可能取的值为0，1，2。  ．

所以，的分布列为

	0	1	2
P

（2）由（1），的数学期望为

（3）由（1），“所选3人中女生人数”的概率为

．

变式4：甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.

（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；

（Ⅱ）求甲、乙两人至少有一人考试合格的概率.

【解析】（Ⅰ）依题意，甲答对试题数ξ的概率分布如下：

ξ	0	1	2	3
P

甲答对试题数ξ的数学期望

Eξ=0×+1×+2×+3×=.

（Ⅱ）设甲、乙两人考试合格的事件分别为A、B，则

P(A)===，P(B)===.

因为事件A、B相互独立，

方法一：

∴甲、乙两人考试均不合格的概率为

P()=P()P()=1－)(1－)=.

∴甲、乙两人至少有一人考试合格的概率为P=1－P()=1－=.

答：甲、乙两人至少有一人考试合格的概率为.

方法二：

∴甲、乙两人至少有一个考试合格的概率为

P=P(A·)+P(·B)+P(A·B)=P(A)P()+P()P(B)+P(A)P(B)

=×+×+×=.

答：甲、乙两人至少有一人考试合格的概率为.

3．（人教A版选修2-3第86页B组2）

若 ，求 。

变式1：随机变量ξ服从正态分布N（0，1），如果P（ξ<1）=0.8413，求P（－1<ξ<0）.

【解析】∵ξ～N（0，1），

∴P（－1<ξ<0）=P（0<ξ<1）=Φ（1）－Φ（0）=0.8413－0.5=0.3413.

变式2：一投资者在两个投资方案中选择一个，这两个投资方案的利润x（万元）分别服从正态分布N（8，3²）和N（6，2²），投资者要求利润超过5万元的概率尽量地大，那么他应选择哪一个方案?

【解析】对第一个方案，有x～N（8，3²），于是P（x>5）=1－P（x≤5）=1－F（5）=1－Φ（）=1－Φ（－1）=1－［1－Φ（1）]=Φ（1）=0.8413.

对第二个方案，有x～N（6，2²），于是P（x>5）=1－P（x≤5）=1－F（5）=1－Φ（）=1－Φ（－0.5）=Φ（0.5）=0.6915.

相比之下，“利润超过5万元”的概率以第一个方案为好，可选第一个方案.

变式3：在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布.已知成绩在90分以上（含90分）的学生有12名.

（Ⅰ）试问此次参赛的学生总数约为多少人？

（Ⅱ）若该校计划奖励竞赛成绩排在前50名的学生，试问设奖的分数线约为多少分？

可供查阅的（部分）标准正态分布表

	0	1	2	3	4	5	6	7	8	9
1.2 1.3 1.4 1.9 2.0 2.1	0.8849 0.9032 0.9192 0.9713 0.9772 0.9821	0.8869 0.9049 0.9207 0.9719 0.9778 0.9826	0.8888 0.9066 0.9222 0.9726 0.9783 0.9830	0.8907 0.9082 0.9236 0.9732 0.9788 0.9834	0.8925 0.9099 0.9251 0.9738 0.9793 0.9838	0.8944 0.9115 0.9265 0.9744 0.9798 0.9842	0.8962 0.9131 0.9278 0.9750 0.9803 0.9846	0.8980 0.9147 0.9292 0.9756 0.9808 0.9850	0.8997 0.9162 0.9306 0.9762 0.9812 0.9854	0.9015 0.9177 0.9319 0.9767 0.9817 0.9857

【解析】：本小题主要考查正态分布，对独立事件的概念和标准正态分布的查阅，考查运用概率统计知识解决实际问题的能力．

【解答】（Ⅰ）设参赛学生的分数为，因为～N(70，100)，由条件知，

P(≥90)＝1－P（<90）＝1－F(90)＝1－＝1－(2)＝1－0.9772＝0.228.

这说明成绩在90分以上（含90分）的学生人数约占全体参赛人数的2.28％，因此，

参赛总人数约为≈526（人）．

（Ⅱ）假定设奖的分数线为x分，则

P(≥x)＝1－P（<x）＝1－F(x)＝1－＝＝0.0951，

即＝0.9049，查表得≈1.31，解得x＝83.1.

故设奖得分数线约为83.1分．

4．（人教A版选修2-3第100页例2）

一只红铃虫的产卵数  和温度  有关，现收集了 7 组观测数据列于表中，试建立  与  之间的回归方程。

温度	21	23	25	27	29	32	35
产卵数个	7	11	21	24	66	115	325

变式1：为了对2006年佛山市中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学(已折算为百分制)、物理、化学分数对应如下表，

学生编号	1	2	3	4	5	6	7	8
数学分数x	60	65	70	75	80	85	90	95
物理分数y	72	77	80	84	88	90	93	95
化学分数z	67	72	76	80	84	87	90	92

(1) 若规定85分(包括85分)以上为优秀，求这8位同学中数学和物理分数均为优秀的概率；

(2) 用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度；

(3) 求y与x、z与x的线性回归方程（系数精确到0.01），并用相关指数比较所求回归模型的效果.

参考数据：，，，，，，，，，，.

解答：(1) 由表中可以看出，所选出的8位同学中，数学和物理分数均为优秀的人数是3人，其概率是.　………………………………………………………………………………………………………3分

(2) 变量y与x、z与x的相关系数分别是

、.　……………………………………………5分

可以看出，物理与数学、化学与数学的成绩都是高度正相关. 　…………………………6分

(3) 设y与x、z与x的线性回归方程分别是、.

根据所给的数据，可以计算出，

.　 ……………………………………………………10分

所以y与x和z与x的回归方程分别是

、.　…………………………………………………………11分

又y与x、z与x的相关指数是、.　……13分

故回归模型比回归模型的拟合的效果好. …14分