高考数学模拟月考试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,试卷满分为150分。考试时间120分。
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合要求的.
1.设集合M={![]() x<5},N={
x<5},N={![]() x>3},那么“
x>3},那么“![]() {
{![]() x
x![]() M或x
M或x ![]() N}是“
N}是“![]() ”
”
的-----------------------------------------------------------------------------------------------( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分条件又非必要条件
2.设Sn是等差数列{an}的前n项和,若=,则等于----------------( )
A B C D
3.将函数![]() 的图象沿
的图象沿![]() 轴向左平移一个单位,再作关于
轴向左平移一个单位,再作关于![]() 轴对称的图形,得到
轴对称的图形,得到![]() 的图象,则------------------------------------------------------------------( )
的图象,则------------------------------------------------------------------( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.曲线![]() 在区间
在区间![]() 上截直线
上截直线![]() 与
与![]() 所得的弦长相等且不为0,则下列对
所得的弦长相等且不为0,则下列对![]() 的描述正确的是---------------------( )
的描述正确的是---------------------( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知实数x、y满足![]()
![]() 的最大值为----------------( )
的最大值为----------------( )
A.![]() B.
B.![]() C.6 D.12
C.6 D.12
6.设O为坐标原点,M(2,1),点N(x,y)满足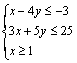 ,则
,则![]() 的最大值为-----------------------------------------------------------------------------------------( )
的最大值为-----------------------------------------------------------------------------------------( )
A.3 B. ![]() C. 12 D.
C. 12 D. ![]()
7.设![]() 是三个非零的向量,且
是三个非零的向量,且![]() 不共线,若实数
不共线,若实数![]() 满足
满足![]() ---( )
---( )
A ![]() B
B ![]() C
C ![]() D
D ![]() 的大小不能确定
的大小不能确定
8.函数f (x)在定义域R内可导,若![]() ,且当
,且当![]() 时,
时,![]() ,设
,设![]() ,则---------------------( )
,则---------------------( )
A.a < b < c B.c < a < b C.c < b < a D.b < c < a
9.已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积最大值是-------------------------------------------( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设函数![]() 的定义如下表,数列
的定义如下表,数列![]() 满足
满足![]() ,对任意自然数
,对任意自然数![]() 均有
均有
![]() ,则
,则![]() 的值为--------------------------------------( )
的值为--------------------------------------( )
|
| 1 | 2 | 3 | 4 | 5 |
|
| 4 | 1 | 3 | 5 | 2 |
(A)1 (B)2 (C)4 (D)5
第Ⅱ卷(非选择题)
二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.
 11、设
11、设![]() 的展开式的各项系数之和为M,且二项式系数之和为N,M—N=992,则展开式中x2项的系数为 .
的展开式的各项系数之和为M,且二项式系数之和为N,M—N=992,则展开式中x2项的系数为 .
12.不等式![]() 的解集是
的解集是
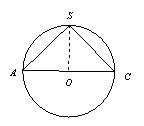
13.正四棱锥![]() 的5个顶点都在球
的5个顶点都在球![]() 的表面上,过球心
的表面上,过球心![]() 的一个截面如图,棱锥的底面边长为1,则球O的表面积为 ;
的一个截面如图,棱锥的底面边长为1,则球O的表面积为 ;
14.已知双曲线![]() 的两条渐近线的夹角为
的两条渐近线的夹角为![]() 。
。
15.在算式:“4×□+1×□=30”的两个□中,分别填入两个自然数,使他们的倒数之和最小,则这两个数应分别为 。
16.一个质点从数轴上原点出发,每次沿数轴向正方向或负方向跳动1个单位,经过10次跳动,质点与原点距离为4,则质点不同的运动方法共有 种(用数字作答).
三、解答题:本大题共5小题,共70分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() = (2,0)所成角为
= (2,0)所成角为![]() ,其中A、B、C是△ABC的内角.
,其中A、B、C是△ABC的内角.
(Ⅰ)求角B的大小;
(Ⅱ)求sinA + sinC的取值范围.
18.(本小题满分14分)在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:
(1)乙连胜四局的概率;(2)丙连胜三局的概率.
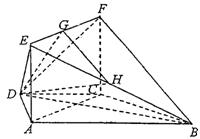
19.(本小题满分14分)如图,在梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() .平面ACFE⊥平面
.平面ACFE⊥平面![]() ,四边形ACFE是矩形,
,四边形ACFE是矩形,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:![]() 平面ACFE;
平面ACFE;
(Ⅱ)当![]() 为何值时,
为何值时,![]() ∥平面
∥平面![]() ?证明你的结论;
?证明你的结论;
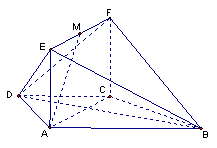 (Ⅲ)求二面角
(Ⅲ)求二面角![]() 的大小.
的大小.
20.(本小题满分14分)过抛物线![]() 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,![]() (1)求点P的轨迹方程;
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
21.(本小题满分16分)
设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且![]() min=
min=![]() ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, ![]() ,
,![]() .
.
(1)求f(x)的解析表达式;
(2)
证明:当n∈N+时, 有bn![]()
![]() .
.
参考答案
一、选择题
1.B 2.A 3.C 4.A 5.A 6.C 7.B 8.B 9.D 10.C
二、填空题
11.-250; 12.(0,2] 13.2π; 14.![]() 或
或![]() ;15.5,10
; 16.
240
;15.5,10
; 16.
240
三、解答题(限于篇幅,每题只给出一种答案,其他答案仿此给分)
17.解:(Ⅰ)∵ ![]() =(sinB,1-cosB) , 且与向量
=(sinB,1-cosB) , 且与向量![]() =(2,0)所成角为
=(2,0)所成角为![]()
∴ ![]() ,
----------------------------------------------------2分
,
----------------------------------------------------2分
∴ tan = , 又∵ 0<B<p Þ 0< < ,-----------------------------4分
∴ = ,∴ B = 。 ----------------------------------------------- 6分
(Ⅱ)由(Ⅰ)可得A + C = ,
∴![]() ----------- 8分
----------- 8分
∵![]() ,∴
,∴![]() ,
------------------------------------------ 10分
,
------------------------------------------ 10分
∴![]() ,
,
当且仅当![]() 。--------------------------------------------
12分
。--------------------------------------------
12分
18.解:(1)当乙连胜四局时,对阵情况如下:
第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
所求概率为![]() =
=![]() ×
×![]() =
=![]() =0.09
=0.09
∴ 乙连胜四局的概率为0.09.-----------------------------------------------------6分
(2)丙连胜三局的对阵情况如下:
第一局:甲对乙,甲胜,或乙胜.
当甲胜时,第二局:甲对丙,丙胜.第三局:丙对乙,丙胜;第四局:丙对甲,丙胜.
当乙胜时,第二局:乙对丙,丙胜;第三局:丙对甲,丙胜;第四局:丙对乙,丙胜.
故丙三连胜的概率![]() =0.4×
=0.4×![]() ×0.5+(1-0.4)×
×0.5+(1-0.4)×![]() ×0.6=0.162.--------14分
×0.6=0.162.--------14分
19.如图,在梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() .平面
.平面![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
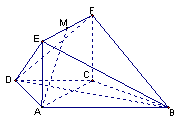 (1)求证:
(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() ∥平面
∥平面![]() ?证明你的结论;
?证明你的结论;
(3)求二面角![]() 的大小.
的大小.
(Ⅰ)证明:在梯形ABCD中,
![]() ,
,
![]() ………………………………3分
………………………………3分
又∵平面ACFE⊥平面ABCD,交线为AC,
![]() ------------------4分
------------------4分
(Ⅱ)当![]() ------------------------5分
------------------------5分
在梯形ABCD中,设![]() ,连结FN,则CN:NA=1:2。
,连结FN,则CN:NA=1:2。
![]()
![]()
![]() ---------------------------------------7分
---------------------------------------7分
又![]()
![]() ------------------------------------------------------9分
------------------------------------------------------9分
(Ⅲ)取EF中点G,EB中点H,连结DG,
|

![]() 的平面角
的平面角
-----------------------12分
在![]()
![]()
![]() .
.![]() 又
又![]()
![]()
即二面角B—EF—D的大小为![]() .
------------------------------------14分
.
------------------------------------14分
20.解法(一):(1)设![]()
由![]() 得:
得:![]() ,
,![]()
![]() ----------------------------------------4分
----------------------------------------4分
直线PA的方程是:![]() 即
即![]() ①
①
同理,直线PB的方程是:![]() ②-------------------6分
②-------------------6分
由①②得: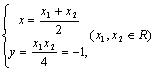
∴点P的轨迹方程是![]() ---------------------------------------------------8分
---------------------------------------------------8分
(2)由(1)得:![]()
![]()
![]()
![]() ,
,![]()
![]() ,所以
,所以![]()
故存在![]() =1使得
=1使得![]() --------------------------------------------------14分
--------------------------------------------------14分
解法(二):(1)∵直线PA、PB与抛物线相切,且![]()
∴直线PA、PB的斜率均存在且不为0,且![]()
设PA的直线方程是![]()
由![]() 得:
得:![]() ----------------------------------------------4分
----------------------------------------------4分
![]() 即
即![]()
即直线PA的方程是:![]()
同理可得直线PB的方程是:![]() -------------------------------------6分
-------------------------------------6分
由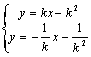 得:
得: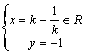
故点P的轨迹方程是![]() -------------------------------------------------8分
-------------------------------------------------8分
(2)由(1)得:![]()
![]() ,
,![]()
![]()
![]()
故存在![]() =1使得
=1使得![]() --------------------------------------------14分
--------------------------------------------14分
21.解:由f(x)是奇函数,得 b=c=0, -------------------3分
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() ------------------6分
------------------6分
(2)
![]() =
=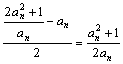 ,
,
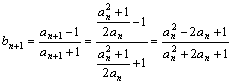 =
=![]() =
=![]() -------------------9分
-------------------9分
∴![]() =
=![]() =
=![]() =…=
=…=![]() ,而b1=
,而b1=![]()
∴![]() =
=![]() ------------------12分
------------------12分
当n=1时,
b1=![]() ,命题成立,
,命题成立,
当n≥2时
∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n
=n
∴![]() <
<![]() ,即 bn≤
,即 bn≤![]() .
-------------------16分
.
-------------------16分