高考数学模拟考试题（文科卷2）
时量120分钟. 满分150分
一、 选择题：（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中有且只有一项是符合题目要求的.）
1、
条件p：“log2x<1”,条件q：“x<2”，则
p是q成立的 （ ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、非充分非必要条件
2、
在等比数列
中，
，
，则
的值为（ ）
A、48 B、72 C、144 D、192
3、 一个容量为20的样本数据，分组后，组别与频数如下：
| 组别 | (10,20] | (20,30] | (30,40] |
| (50,60] | (60,70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
则样本在
上的频率为 （ ）
A、12% B、40% C、60% D、70%
4、
设函数
是定义在实数集上的以3为周期的奇函数，若
，则 （ ）
A、
B、且
C、
D、
5、
过点
作圆
的两切线，设两切点为
、
，圆心为
，则过、、的圆方程是
（
）
A、
B、
C、
D、
6、
已知椭圆
与双曲线
有相同的准线，则动点
的轨迹为（ ）
A、椭圆的一部分 B、双曲线的一部分
C、抛物线的一部分 D、直线的一部分
7、
把函数
的图象沿直线
的方向向右下方移动
个单位长度，得到的图形恰好是函数
的图象，则是（ ）
A、
B、
C、
D、 
8、
若圆x2+y2=r2(r>0)至少能盖住函数
的一个最大值点和一个最小值点，则r的取值范围是（ ）
A、
B、
C、
D、以上都不对
9、 从6名教师中选派4人分别到A、B、C、D四个农村学校去支教，要求每个学校有一人支教，每人只能支援一个学校，由于种种原因，教师甲不能去A校，教师乙不能去B校，则不同的选派方案共有 （ ）
A、360种 B、300种 C、252种 D、192种
10、
已知A、B、C三点共线，O是这条直线外一点，设
且存在实数m，使
0成立，则点A分
的比为（ ）
A、 
B、 
C、 
D、 
第Ⅱ卷（非选择题共100分）
二、填空题：（本大题共5小题，每小题4分，共20分），
11、若椭圆
上一点
到右焦点
的距离为
，则点P到
轴的距离为 。
12．已知向量a、b满足：（a－b）·（2a+b）=－4，且a=2，b=4，则a与b的夹角等于 .
13．函数
是定义在R上以3为周期的奇函数, 若
, 
. 则实数a的取值范围是________________.
14.如果直线
与圆
相交于
两点,且点关于直线
对称,则不等式组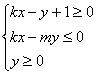
所表示的平面区域的面积为________.
15、已知数列
的首项
，
是其前
项的和，且满足
，则此数列的通项公式为
| 学校_________________班级 姓名 学号 |
三、解答题：（本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.）
16．（12分）在△ABC中，a,b,c分别是角A、B、C的对边，且
.
（1）求角A的大小； （2）若a=
,b+c=3,求b和c的值.
17. (12分) 命题甲: 
R, 关于x的方程
有两个非零实数解; 命题乙:
R, 关于x的不等式
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
18、（14分）已知等差数列的前4项的和为10，且
成等比数列。
（I）求通项公式
。
（II）设
，求数列
的前项的和。
19、（14分）已知直线
与抛物线：
相交于不同的两点A，B
（I）求实数
的取值范围；
（II）在抛物线上是否存在一个定点，对（I）中任意的的值，都有直线
与
的斜率互为相反数？若存在，求出点的坐标；若不存在，试说明理由
|
|
学校_________________班级 姓名 学号 20．（14分）
已知定义在R上的函数满足：对于任意实数
，恒有
，且当
时，
（1）求证：
当
时，有
；
（2）试判断在且R上的单调性，并证明你的结论；
（3）若实数x、y满足：
，且
，
求z=x+y的取值范围.
21、（14分）已知函数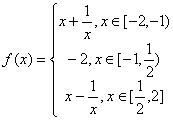
（I）求的值域；
（II）设函数
，若对于任意
总存在
，使得
成立，求实数
的取值范围。
（文科）2答案
YCY
一、选择题（每小题5分，共50分）
BDCCA、DABCA
二.填空题（每小题4分，共20分）
11．
； 12。120°； 13．
； 14。
； 15．
。
三、解答题：（本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤）.
16．解：（1）在△ABC中有B+C=π-A，由条件可得 4[1-cos（B+C）]-4cos2A+2=7.
又∵ cos（B+C）=-cosA， ∴4 cos2A-4cosA+1=0
解得：cosA=
, 又A∈（0，π），∴ A=
.
（2）由cosA= 知 
=, 即
.
又a=
，b+c=3，代入得 
.
由
或 
17．解：当甲真时，设
，即两函数图象有两个交点.
则
当乙真时，
时 满足 或
也满足
则
∴当甲乙有但仅有一个为真命题时，即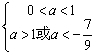
或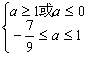
∴
18、解：（I）由题意知：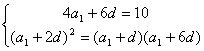
解得：
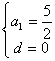
或 
或 
（II）当
时，数列是首项为，公比为8等比数列，
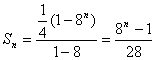
当时，
综上，
或
19解：（I）
抛物线与直线有两不同的交点，
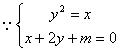有两个不同的解，即方程
有两个不同的解 
即：
（I）
设
，（
，
，
由
得 
假设在抛物线上存在定点使得直线与的斜率互为相反数。
即：
即：
得 
即：存在定点
使得直线与的斜率互为相反数。
20．（1）证：
设
…………………………………（4分）
（2）解：设
在R上单调递减.……………………………………………………（8分）
（3）
①………（10分）
又
②………（11分）
由同时满足①、②的点（
的集合求Z，
∴Z∈[4，6]………………………………（14分）
21解：（I）当
时，
在
上是增函数，此时
当
时，
当
时，
在
上是增函数，此时
的值域为
……………………………6 分
（II）（1）若
，
对于任意
，
，不存在 使得 成立
（2）若当
时， 
在[-2，2]是增函数，
任给，，
若存在，使得成立，
则
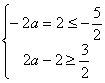
……………………………………10分
（3）若
，在[-2，2]是减函数，
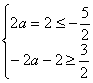
综上，实数的取值范围是
………………………………14