专题4 平面向量(1)
一、课前练习:
1.( 05重庆)已知A(3,1),B(6,1),C(4,3),D为线段BC的中点,则向量![]() 与
与![]() 的夹角为 ( )
的夹角为 ( )
A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
2.( 04全国2)已知平面上直线l的方向向量e=![]() 点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则
点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则![]() e,其中
e,其中![]() =
=
(A)![]() (B)
(B)![]() (C)2 (D)-2
(C)2 (D)-2
3.( 05湖北)已知向量![]() 不超过5,则k的取值范围是
.
不超过5,则k的取值范围是
.
二、例题选讲:
例1.( 05山东)已知向量![]() 和
和![]() 且
且![]() 求
求![]() 的值.
的值.
例2. (05福建)已知方向向量为v=(1,![]() )的直线l过点(0,-2
)的直线l过点(0,-2![]() )和椭圆C:
)和椭圆C:![]() 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(1) 求椭圆C的方程;

(备)例3.( 03天津)已知常数a>0,向量c=(0,a),i=(1,0).经过原点O以c+li为方向向量的直线与经过定点A(0,a)以i-2lc为方向向量的直线相交于点P,其中l∈R.试问:是否存在两个定点E、F,使得 PE + PF 为定值.若存在,求出E、F的坐标;若不存在,说明理由.
三、课堂练习:
1. (05山东)已知向量![]() ,且
,且![]()
![]() 则一定共线的三点是 ( )
则一定共线的三点是 ( )
A.A、B、D B.A、B、C C.B、C、D D.A、C、D
2. (05广东)已知向量![]() 则x=
.
则x=
.
3. (04湖南)已知向量a=![]() ,向量b=
,向量b=![]() ,则2a-b的最大值是
.
,则2a-b的最大值是
.
四、课后练习:
1.
条件甲:“四边形![]() 是平行四边形”是条件乙:“
是平行四边形”是条件乙:“![]() ”成立的( )
”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
2.
已知平面上直线![]() 的方向向量
的方向向量![]() ,点O(0,0)和A(1,-2)在
,点O(0,0)和A(1,-2)在![]() 上的射影分别是O1和A1,则
上的射影分别是O1和A1,则![]() =
=![]()
![]() ,其中
,其中![]() =( )
=( )
A.![]() B.-
B.-![]() C.2 D.-2
C.2 D.-2
3. 下列条件中,不能确定三点A、B、P共线的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.
在直角坐标系中,O是原点,![]() =(-2+cosθ,-2+sinθ) (θ∈R),动点P在直线x=3上运动,若从动点P向Q点的轨迹引切线,则所引切线长的最小值为 ( )
=(-2+cosθ,-2+sinθ) (θ∈R),动点P在直线x=3上运动,若从动点P向Q点的轨迹引切线,则所引切线长的最小值为 ( )
A. 4 B. 5 C. 2![]() D.
D.
![]()
5.(05全国2)点P在平面上作匀速直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为v个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为 ( )
A.(-2,4) B.(-30,25) C.(10,-5) D.(5,-10)
6.( 04天津)若平面向量![]() 与向量
与向量![]() 的夹角是
的夹角是![]() ,且
,且![]() ,则
,则![]() (A)
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
7. (04广东)已知平面向量![]() =(3,1),
=(3,1),![]() =(x,–3),且
=(x,–3),且![]() ,则x=
(A)-3
(B)-1
(C)1
(D)3
,则x=
(A)-3
(B)-1
(C)1
(D)3
8. (04上海)已知点A(1, -2),若向量![]() 与
与![]() ={2,3}同向,
={2,3}同向,
![]() =2
=2![]() ,则点B的坐标为
.
,则点B的坐标为
.
9. (05全国3)已知向量![]() ,且A、B、C三点共线,则k= .
,且A、B、C三点共线,则k= .
10. (03上海)在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知AB=2OA,且点B的纵坐标大于零.(1)求向量![]() 的坐标; (2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
的坐标; (2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
11.已知△OFQ的面积为S,且![]() =1⑴若
=1⑴若![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
⑵设︱![]() ︱=C(c≥2),S=
︱=C(c≥2),S=![]() C,若以O为中心,F为焦点的椭圆经过点Q,当︱
C,若以O为中心,F为焦点的椭圆经过点Q,当︱![]() ︱取最小值时,求此时椭圆的方程.
︱取最小值时,求此时椭圆的方程.
专题4 平面向量(2)
一、课前练习:
1.(05北京)![]() ,则向量
,则向量![]() 的夹角为 ( )
的夹角为 ( )
A.30° B.60° C.120° D.150°
2.(05浙江)已知向量![]() ≠
≠![]() ,
,![]() =1,对任意t∈R,恒有
=1,对任意t∈R,恒有![]() -t
-t![]() ≥
≥![]() -
-![]() ,则( )
,则( )
A.![]() ⊥
⊥![]() B.
B.![]() ⊥(
⊥(![]() -
-![]() ) C.
) C.![]() ⊥(
⊥(![]() -
-![]() ) D.(
) D.(![]() +
+![]() )⊥(
)⊥(![]() -
-![]() )
)
3.(04浙江)已知平面上三点A、B、C满足![]() 则
则![]() 的值等于 .
的值等于 .
二、例题选讲:
例1. 已知向量![]()
(1)求![]() (2)若
(2)若![]() 的最小值为
的最小值为![]() 的值.
的值.
例2.(05上海卷)在直角坐标平面中,已知点![]() ,其中
,其中![]() 是正整数,对平面上任一点
是正整数,对平面上任一点![]() ,记
,记![]() 为
为![]() 关于点
关于点![]() 的对称点,
的对称点,![]() 为
为![]() 关于点
关于点![]() 的对称点,...,
的对称点,...,![]() 为
为![]() 关于点
关于点![]() 的对称点。(Ⅰ)求向量
的对称点。(Ⅰ)求向量![]() 的坐标;(Ⅱ)当点
的坐标;(Ⅱ)当点![]() 在曲线C上移动时,点
在曲线C上移动时,点![]() 的轨迹是函数
的轨迹是函数![]() 的图象,其中
的图象,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]() 时,
时,![]() 。求以曲线C为图象的函数在
。求以曲线C为图象的函数在![]() 上的解析式;
上的解析式;
(Ⅲ)对任意偶数![]() ,用
,用![]() 表示向量
表示向量![]() 的坐标。
的坐标。
(备)例3.(04福建)设函数f(x)= ![]() ·
·![]() ,其中向量
,其中向量![]() =(2cosx,1),
=(2cosx,1),![]() =(cosx,
=(cosx, ![]() sin2x),x∈R.(Ⅰ)若f(x)=1-
sin2x),x∈R.(Ⅰ)若f(x)=1-![]() 且x∈[-
且x∈[-![]() ,
,![]() ],求x;(Ⅱ)若函数y=2sin2x的图象按向量
],求x;(Ⅱ)若函数y=2sin2x的图象按向量![]() =(m,n)(m<
=(m,n)(m<![]() )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
三、课堂练习:
1.(05江西)已知向量![]() ( )
( )
A.30° B.60°
C.120° D.150°
2.(04湖北)已知![]() 为非零的平面向量. 甲:
为非零的平面向量. 甲:![]()
(A)甲是乙的充分条件但不是必要条件
(B)甲是乙的必要条件但不是充分条件
(C)甲是乙的充要条件
(D)甲既不是乙的充分条件也不是乙的必要条件
3.(00上海卷)已知向量![]() (-1,2)、
(-1,2)、![]() =(3,m),若
=(3,m),若![]() ┴
┴![]() ,则m=
。
,则m=
。
四、课后练习:
1.(04福建)已知![]() 、
、![]() 是非零向量且满足(
是非零向量且满足(![]() -2
-2![]() ) ⊥
) ⊥![]() ,(
,(![]() -2
-2![]() ) ⊥
) ⊥![]() ,则
,则![]() 与
与![]() 的夹角是 (A)
的夹角是 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.(04重庆)若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则向量
,则向量![]() 的模为
(A)2 (B)4
(C)6 (D)12
的模为
(A)2 (B)4
(C)6 (D)12
3.(00天津)设![]() 、
、![]() 、
、![]() 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①![]() ②
②![]() ③
③![]() 不与
不与![]() 垂直
垂直
④![]() 中,是真命题的有
中,是真命题的有
(A) ①② (B) ②③ (C) ③④ (D) ②④
4.(04全国1)已知a、b均为单位向量,它们的夹角为60°,那么a+3b= (A)![]() (B)
(B)![]() (C)
(C)![]() (D)4
(D)4
5.若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则向量
,则向量![]() 的模为( )
的模为( )
A. 2 B. 4 C. 6 D. 12
6.(04全国4)向量a、b满足(a-b)·(2a+b)=-4,且a=2,b=4,则a与b夹角的
余弦值等于
7.(02上海)已知向量![]() 和
和![]() 的夹角为120°,且
的夹角为120°,且![]() ,
,![]() ,则
,则![]() = 。
= 。
8.(04江苏卷)平面向量a,b中,已知a=(4,-3),![]() =1,且a·b=5,则向量b=__________.
=1,且a·b=5,则向量b=__________.
9设![]() =(3,1),
=(3,1),![]() =(-1,2),
=(-1,2),![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,试求满足
,试求满足![]() +
+![]() =
=![]() 的
的![]() 的坐标,其中O为坐标原点。
的坐标,其中O为坐标原点。
10.(05湖北)已知向量![]() 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
11.椭圆的两焦点分别为![]() 、
、![]() ,直线
,直线![]() 是椭圆的一条准线.
是椭圆的一条准线.
(1)求椭圆的方程;(2)设点![]() 在椭圆上,且
在椭圆上,且![]() ,求
,求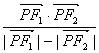 的最大值和最小值.
的最大值和最小值.
专题4 平面向量(1)答案
一、课前练习:1.C 2.D 3.[-6,2]
二、例题选讲:
例1.解法一:
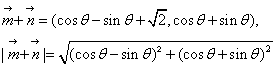
![]()
由已知![]() 得
得![]() 又
又![]()
所以![]()
![]()
解法二:![]()
![]()
![]() 由已知
由已知![]()
例2.本小题主要考查直线、椭圆及平面向量的基本知识,平面解析几何的基本方法和综合解题能力.
(I)解法一:直线![]() , ① 过原点垂直
, ① 过原点垂直![]() 的直线方程为
的直线方程为![]() , ②
, ②
解①②得![]() ∵椭圆中心(0,0)关于直线
∵椭圆中心(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
![]() ∵直线
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
![]() 故椭圆C的方程为
故椭圆C的方程为![]() ③
③
解法二:直线![]() .设原点关于直线
.设原点关于直线![]() 对称点为(p,q),则
对称点为(p,q),则
![]() 解得p=3.∵椭圆中心(0,0)关于直线
解得p=3.∵椭圆中心(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,![]() ∵直线
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).![]() 故椭圆C的方程为
故椭圆C的方程为![]() ③
③
(II)解法一:设M(![]() ),N(
),N(![]() ).当直线m不垂直
).当直线m不垂直![]() 轴时,直线
轴时,直线![]() 代入③,整理得
代入③,整理得
![]()
![]()
![]()
点O到直线MN的距离![]()
![]()
即 ![]()
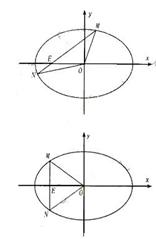
![]() 即
即![]() 整理得
整理得![]() 当直线m垂直x轴时,也满足
当直线m垂直x轴时,也满足![]() .故直线m的方程为
.故直线m的方程为![]() 或
或![]() 或
或![]()
经检验上述直线均满足![]() .
.
所以所求直线方程为![]() 或
或![]()
![]()
解法二:设M(![]() ),N(
),N(![]() ).
).
当直线m不垂直![]() 轴时,直线
轴时,直线![]() 代入③,整理得
代入③,整理得![]()
![]() ∵E(-2,0)是椭圆C的左焦点,∴MN=ME+NE
∵E(-2,0)是椭圆C的左焦点,∴MN=ME+NE
=![]() 以下与解法一相同.
以下与解法一相同.
解法三:设M(![]() ),N(
),N(![]() ).设直线
).设直线![]() ,代入③,整理得
,代入③,整理得![]()
![]()
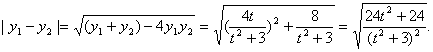
![]() 即
即 ![]()
![]()
![]()
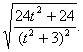 ∴
∴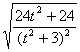 =
=![]() ,整理得
,整理得![]() 解得
解得![]() 或
或![]() 故直线m的方程为
故直线m的方程为![]() 或
或![]() 或
或![]() 经检验上述直线方程为
经检验上述直线方程为![]()
所以所求直线方程为![]() 或
或![]() 或
或![]()
例3.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵ i=(1,0),c=(0,a),∴ c+li=(l,a),i-2lc=(1,-2la).因此,直线OP和AP的方程为ly=ax 和 y-a=-2lax.消去参数l,得点P(x,y)的坐标满足方程y(y-a)=-2a2x2,
整理得 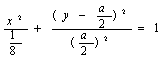 .
①
.
①
因为a>0,所以得:(ⅰ)当![]() 时,方程①是圆方程,故不存在合乎题意的定点E和F;(ⅱ)当
时,方程①是圆方程,故不存在合乎题意的定点E和F;(ⅱ)当![]() 时,方程①表示椭圆,焦点
时,方程①表示椭圆,焦点![]() 和
和![]() 为合乎题意的两个定点:(ⅲ)当
为合乎题意的两个定点:(ⅲ)当![]() 时,方程①也表示椭圆,焦点
时,方程①也表示椭圆,焦点![]() 和
和![]() 为合乎题意的两个定点.
为合乎题意的两个定点.
三、课堂练习:1.A 2.4 3. 4
四、课后练习:
1.A
2.D 3.D 4.C 5.C 6.A 7.C 8. (5,4) 9.![]()
10. 解:(1)设![]() ,则由
,则由![]() 即
即![]() 得
得![]() 或
或![]()
因为![]() 所以 v-3>0,得 v=8,故
所以 v-3>0,得 v=8,故 ![]()
(2)由![]() 得B(10,5),于是直线OB方程:
得B(10,5),于是直线OB方程:![]() 由条件可知圆的标准方程为:(x-3)2+(y+1)2=10,得圆心(3,-1),半径为
由条件可知圆的标准方程为:(x-3)2+(y+1)2=10,得圆心(3,-1),半径为![]() 设圆心(3,-1)关于直线OB的对称点为(x,y),则
设圆心(3,-1)关于直线OB的对称点为(x,y),则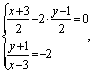 得
得![]() 故所求圆的方程为(x-1)2+(y-3)2=10.
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称的两点,则
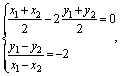 得
得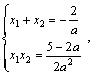 即x1、x2为方程
即x1、x2为方程![]() 的两个相异实根,
的两个相异实根,
于是由![]() 得
得![]() 故当
故当![]() 时,抛物线y =ax2-1上总有关于直线OB对称的两点.
时,抛物线y =ax2-1上总有关于直线OB对称的两点.
11.解:⑴由已知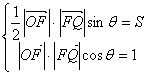 ∴tan
∴tan![]() =2S,由
=2S,由![]() <S<2,得1<tan
<S<2,得1<tan![]() <4.又
<4.又![]() ∈(0,
∈(0,![]() )∴
)∴![]() ⑵以O为原点,
⑵以O为原点,![]() 所在直线为X轴建立坐标系,设所求∵S△OFQ=
所在直线为X轴建立坐标系,设所求∵S△OFQ=![]() ︱
︱![]() ︱•︱y0︱=
︱•︱y0︱=![]() c,∴︱y0︱=
c,∴︱y0︱=![]() ,∵
,∵![]() =1,∴(c,0)•(x0-c,y0)=1,解得x0=c+
=1,∴(c,0)•(x0-c,y0)=1,解得x0=c+![]() .∴︱
.∴︱![]() ︱=
︱=![]() =
=![]() ,注意到当c≥2时,c+
,注意到当c≥2时,c+![]() 随c的增大而增大,因此当且仅当c=2时,︱
随c的增大而增大,因此当且仅当c=2时,︱![]() ︱有最小值,此时点Q坐标为(
︱有最小值,此时点Q坐标为(![]() ,-
,-![]() )或(
)或(![]() ,
,![]() )∴
)∴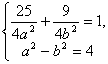 解得
解得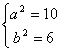 ,故所求椭圆方程为
,故所求椭圆方程为![]()
专题4 平面向量(2)答案
一、课前练习:1.C 2.C 3. --25
二、例题选讲:
例1. 解:(1)![]() .
.
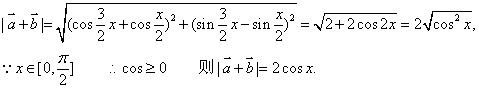
(2)![]()
当λ<0时,当且仅当cosx=0时,f(x)取最小值-1,与已知矛盾.
当0≤λ≤1时,当且仅当cosx=λ时,f(x)取最小值-1-2λ2,由已知得:-1-2λ2=-![]() ,解得:λ=
,解得:λ=![]() .当λ>1时,当且仅当cosx=1时,f(x)取得最小值1-4λ,由已知得:
.当λ>1时,当且仅当cosx=1时,f(x)取得最小值1-4λ,由已知得:![]() 矛盾.综上所述:λ=
矛盾.综上所述:λ=![]() 为所求.
为所求.
例2.解:(1)设点![]() ,A0关于点P1的对称点A1的坐标为
,A0关于点P1的对称点A1的坐标为![]()
A1关于点P2的对称点A2的坐标为![]() ,所以,
,所以,![]()
(2)解法一![]() 的图象由曲线C向右平移2个单位,再向上平移4个单位得到。因此,基线C是函数
的图象由曲线C向右平移2个单位,再向上平移4个单位得到。因此,基线C是函数![]() 的图象,其中
的图象,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]()
解法二设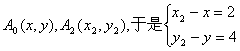
若![]()
当![]()
![]()
(3)![]()
由于![]() ,
,
![]()
例3.本小题主要考查平面向量的概念和计算,三角函数的恒等变换及其图象变换的基本技能,考查运算能力.
解:(Ⅰ)依题设,f(x)=2cos2x+![]() sin2x=1+2sin(2x+
sin2x=1+2sin(2x+![]() ).由1+2sin(2x+
).由1+2sin(2x+![]() )=1-
)=1-![]() ,得sin(2 x +
,得sin(2 x +![]() )=-
)=-![]() .∵-
.∵-![]() ≤x≤
≤x≤![]() ,∴-
,∴-![]() ≤2x+
≤2x+![]() ≤
≤![]() ,∴2x+
,∴2x+![]() =-
=-![]() ,即x=-
,即x=-![]() .
.
(Ⅱ)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(Ⅰ)得 f(x)=2sin2(x+![]() )+1.∵m<
)+1.∵m<![]() ,∴m=-
,∴m=-![]() ,n=1.
,n=1.
三、课堂练习:1.C 2.B 3. 4
四、课后练习:1.B 2.C 3.D 4.C 5.C
6.![]() 7. 13 . 8.
7. 13 . 8.![]()
9. (11,6);
10.本小题主要考查平面向量数量积的计算方法、利用导数研究函数的单调性,以及运用基本函数的性质分析和解决问题的能力。
解法1:依定义![]()
![]()
![]()

开口向上的抛物线,故要使![]() 在区间(-1,1)上恒成立
在区间(-1,1)上恒成立![]()
![]()
![]()
![]() .
.
解法2:依定义![]()
![]()
![]() 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,![]()
![]()
11.解(1)依据题意,设椭圆的方程为![]() ,则由
,则由
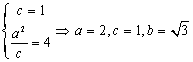 ,椭圆方程为
,椭圆方程为![]() .
.
(2)因为![]() 在椭圆上,故
在椭圆上,故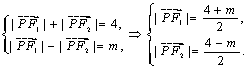
![]()
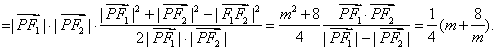
由平面几何知识得 ![]() ,即
,即![]() ,所以
,所以![]() .
.
令![]() ,设
,设![]() 且
且![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上是单调递减的,从而当
上是单调递减的,从而当![]() 时,原式取得最大值
时,原式取得最大值![]() ,当
,当![]() 时原式取得最小值
时原式取得最小值![]() .
.