高考数学招生适应性考试文科卷
考试时间:2007年4月120分钟。
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)
参考公式:如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P, V=![]()
那么n次独立重复试验中恰好发生k次的概率 其中R表示不的半径
Pn(k)=C![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,保有一项是符合题目要求的。
(1)已知集合![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)已知![]() 且
且![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)7
(D)7
(4)已知向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)若数列![]() 中,
中,![]() ,且对任意的正整数
,且对任意的正整数![]() 、
、![]() 都有
都有![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)若直线![]() 与直线
与直线![]() 平行,则
平行,则![]() 的值等于
的值等于
(A) 1 (B)![]() (C)1或
(C)1或![]() (D)
(D)![]() 或
或![]()
(7)曲线![]() 与曲线
与曲线![]() 有
有
(A)相同的焦距 (B)相同的离心率 (C)相同的焦点 (D)相同的准线
(8)![]() 的展开式中的常数项是
的展开式中的常数项是
(A)![]() (B)15 (C)
(B)15 (C)![]() (D)30
(D)30
(9)函数![]() 的最小值是
的最小值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
(10)对于任意的直线![]() 与平面
与平面![]() ,在平面
,在平面![]() 内必有直线
内必有直线![]() ,使直线
,使直线![]() 与
与![]()
(A)平行 (B)相交 (C)互为异面直线 (D)垂直
(11)若不等式![]() 对任意的
对任意的![]() 、
、![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为
的最小值为
(A)1 (B)4 (C)9 (D)14
(12)若![]() 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的的取值范围是
的的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:(本大题共4小题,每小题4分,共16分)把答案填在题中横线上。
(13)![]() 的值为
。
的值为
。
(14)在一次联欢会上,到会的男生比女生多12人。从这些人中随机挑选一人表演节目,若选到女生的概率为![]() ,则参加联欢会的人数共有
人。
,则参加联欢会的人数共有
人。
(15)若实数![]() 、
、![]() 满足
满足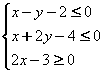 ,则
,则![]() 的最大值为
。
的最大值为
。
(16)将正方形![]() 沿对角线
沿对角线![]() 折成直二面角,给出下列四个结论:①
折成直二面角,给出下列四个结论:①![]() ;②
;②![]() 与
与![]() 所成角为
所成角为![]() ;③
;③![]() 为正三角形;④
为正三角形;④![]() 与平面
与平面![]() 所成角为
所成角为![]() 。其中正确的结论是 (填写结论的序号)。
。其中正确的结论是 (填写结论的序号)。
三、解答题:(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分12分)已知向量![]() 且
且![]() ,
,
(Ⅰ)若![]() 与
与![]() 是两个共线向量,求
是两个共线向量,求![]() 的值;
的值;
(Ⅱ)若![]() ,求函数
,求函数![]() 的最小值及相应的
的最小值及相应的![]() 的值。
的值。
(18)(本小题满分12分)杏坛中学组织高二年级4个班的学生到汉方制药厂、贵阳钢厂、贵阳轮胎厂进行社会实践,规定每个班只能在这3个厂中任选择一个,假设每个班选择每个厂的概率是等可能的。
(Ⅰ)求3个厂都有班级选择的概率;
(Ⅱ)求恰有2个厂有班级选择的概率。
(19)(本小题满分12分)已知函数![]() 满足
满足![]() ,
,
(Ⅰ)求![]() 、
、![]() 的值及函数
的值及函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
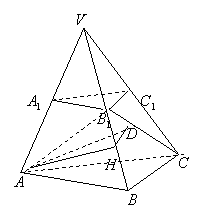
(20)(本小题满分12分)如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面,等边三角形
的底面,等边三角形![]() 所在平面与面
所在平面与面![]() 垂直,且
垂直,且![]() ,设
,设![]() 。
。
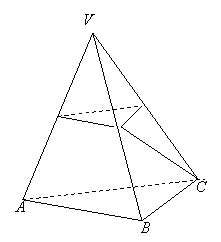 (Ⅰ)证明:
(Ⅰ)证明:![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(Ⅱ)求点![]() 与平面
与平面![]() 的距离;
的距离;
|
|
|
(21)(本小题满分12分)已知定点![]() ,动点
,动点![]() 满足条件:
满足条件:![]() ,点
,点![]() 的轨迹是曲线
的轨迹是曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点。如果
两点。如果![]() 。
。
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)若曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值。
的值。
(22)(本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]()
(Ⅰ)写出![]() 与
与![]() 的递推关系式(
的递推关系式(![]() );
);
(Ⅱ)求![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
[参考答案]
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)
参考公式:如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P, V=![]()
那么n次独立重复试验中恰好发生k次的概率 其中R表示不的半径
Pn(k)=C![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,保有一项是符合题目要求的。
(1)已知集合![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析:由题知![]() ,故选择C。
,故选择C。
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析:由正弦定理得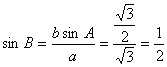 ,因
,因![]() ,故
,故![]() 故选择C。
故选择C。
(3)已知![]() 且
且![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)7
(D)7
解析:由![]() 且
且![]() 得
得![]() ,
,
∴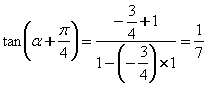 ,故选择C。
,故选择C。
(4)已知向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析: ,故选择B。
,故选择B。
(5)若数列![]() 中,
中,![]() ,且对任意的正整数
,且对任意的正整数![]() 、
、![]() 都有
都有![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析:由题得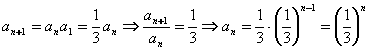 ,故选择C。
,故选择C。
(6)若直线![]() 与直线
与直线![]() 平行,则
平行,则![]() 的值等于
的值等于
(A) 1 (B)![]() (C)1或
(C)1或![]() (D)
(D)![]() 或
或![]()
解析:由题得![]() ,逐一检验,可知只有
,逐一检验,可知只有![]() 符合条件,故选择A。
符合条件,故选择A。
(7)曲线![]() 与曲线
与曲线![]() 有
有
(A)相同的焦距 (B)相同的离心率 (C)相同的焦点 (D)相同的准线
解析:由![]() 知这是焦点在
知这是焦点在![]() 轴上的椭圆,由
轴上的椭圆,由![]() 得
得![]() ,即这是焦点在
,即这是焦点在![]() 轴上的双曲线,故排除B、C、D,选择A。
轴上的双曲线,故排除B、C、D,选择A。
(8)![]() 的展开式中的常数项是
的展开式中的常数项是
(A)![]() (B)15 (C)
(B)15 (C)![]() (D)30
(D)30
解析:由题![]() ,故常数项为
,故常数项为![]() ,故选择B。
,故选择B。
(9)已知函数![]() ,则
,则![]() 的值域是
的值域是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析:由题![]() ,在同一坐标系中画出
,在同一坐标系中画出![]() 与
与![]() 的图象,由数形结合,可得
的图象,由数形结合,可得![]() ,故选择C。
,故选择C。
(10)对于任意的直线![]() 与平面
与平面![]() ,在平面
,在平面![]() 内必有直线
内必有直线![]() ,使直线
,使直线![]() 与
与![]()
(A)平行 (B)相交 (C)互为异面直线 (D)垂直
解析:由题选择D。A错,原因是如![]() ;B错,原因是如
;B错,原因是如![]() ∥
∥![]() ;C错,原因是如
;C错,原因是如![]() 。
。
(11)若不等式![]() 对任意的
对任意的![]() 、
、![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为
的最小值为
(A)1 (B)4 (C)9 (D)14
解析:由题得![]()
∴![]() ,故选择C。
,故选择C。
(12)若![]() 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的的取值范围是
的的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解析:由题得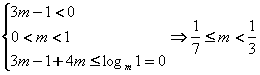 ,故选择D。
,故选择D。
二、填空题:(本大题共4小题,每小题4分,共16分)把答案填在题中横线上。
(13)![]() 的值为 。
的值为 。
解析:![]()
![]()
(14)在一次联欢会上,到会的男生比女生多12人。从这些人中随机挑选一人表演节目,若选到女生的概率为![]() ,则参加联欢会的人数共有
人。
,则参加联欢会的人数共有
人。
 解析:设女生有
解析:设女生有![]() 人,由题得
人,由题得![]() 。
。
|
 ,则
,则![]()
|
|
(16)将正方形![]() 沿对角线
沿对角线![]() 折成直二面角,给出下列四个结论:①
折成直二面角,给出下列四个结论:①![]() ;②
;②![]() 与
与![]() 所成角为
所成角为![]() ;③
;③![]() 为正三角形;④
为正三角形;④![]() 与平面
与平面![]() 所成角为
所成角为![]() 。其中正确的结论是
(填写结论的序号)。
。其中正确的结论是
(填写结论的序号)。
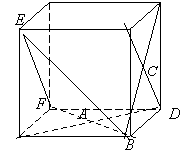 解析:法1建立空间直角坐标系,通过计算可得正确的结论为①②③。
解析:法1建立空间直角坐标系,通过计算可得正确的结论为①②③。
法2,如右图,将空间四边形放置到正方体中,由三垂线定理知①正确;由异面直线所成角知,![]() 与
与![]() 所成角即直线
所成角即直线![]() 与
与![]() 所成角,因
所成角,因![]() 为正三角形,故
为正三角形,故![]() 与
与![]() 所成角为
所成角为![]() ,所以②正确;设
,所以②正确;设![]() ,则
,则![]() ,
,![]() ,故③正确;
,故③正确;![]() 与平面
与平面![]() 所成角为
所成角为![]() ,故④错。
,故④错。
三、解答题:(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分12分)已知向量![]() 且
且![]() ,
,
(Ⅰ)若![]() 与
与![]() 是两个共线向量,求
是两个共线向量,求![]() 的值;
的值;
(Ⅱ)若![]() ,求函数
,求函数![]() 的最小值及相应的
的最小值及相应的![]() 的值。
的值。
解析:(Ⅰ)∵![]() ∥
∥![]()
∴![]() ,
,
又∵![]()
∴![]()
∴![]() 即
即![]()
∴![]() 。
。
(Ⅱ)![]()
当且仅当![]() 即
即![]() 时取到等号。
时取到等号。
故函数![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 。
。
(18)(本小题满分12分)杏坛中学组织高二年级4个班的学生到汉方制药厂、贵阳钢厂、贵阳轮胎厂进行社会实践,规定每个班只能在这3个厂中任选择一个,假设每个班选择每个厂的概率是等可能的。
(Ⅰ)求3个厂都有班级选择的概率;
(Ⅱ)求恰有2个厂有班级选择的概率。
解析:(Ⅰ)由题杏坛中学的4个班选择3个厂进行社会实践,可能出现的结果共有![]() 种结果,由于这些结果出现的可能性相等,3个厂都有班级选择的可能出现的结果数为
种结果,由于这些结果出现的可能性相等,3个厂都有班级选择的可能出现的结果数为![]() ,设“3个厂都有班级选择”为事件
,设“3个厂都有班级选择”为事件![]() ,则事件
,则事件![]() 的概率为
的概率为![]() 。
。
(Ⅱ)记“恰有2个厂有班级选择”和“恰有1个厂有班级选择”为事件![]() ,则
,则![]()
∴![]() 。
。
(19)(本小题满分12分)已知函数![]() 满足
满足![]() ,
,
(Ⅰ)求![]() 、
、![]() 的值及函数
的值及函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
解析:(Ⅰ)![]() ,由
,由![]() 得
得
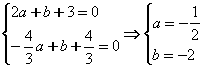
∴![]() ,故
,故![]() 或
或![]()
故![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() 。
。
(Ⅱ)法1:当![]() 变化时,
变化时,![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
| 1 |
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
可见![]() ,
,![]() ,当
,当![]() 时,
时,![]() 为极大值,而
为极大值,而![]() ,则
,则![]() 为最大值,故要使不等式
为最大值,故要使不等式![]() 在
在![]() 时恒成立,只须
时恒成立,只须![]() ,即
,即![]()
![]() 即
即![]()
解得![]() 或
或![]()
∴![]() 的取值范围为
的取值范围为![]() 。
。
法2: 由(Ⅰ)得![]()
![]() 即
即![]()
对![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 不等式
不等式![]() 恒成立,
恒成立,
构造函数![]() ,只须
,只须![]()
∵![]() ,令
,令![]() 得
得![]() 和
和![]()
![]()
![]()
∴![]() ,解不等式
,解不等式![]() 得
得![]() 或
或![]()
 ∴
∴![]() 的取值范围为
的取值范围为![]() 。
。
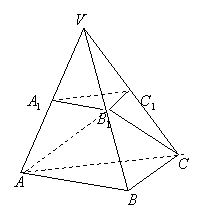
(20)(本小题满分12分)如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面,等边三角形
的底面,等边三角形![]() 所在平面与面
所在平面与面![]() 垂直,且
垂直,且![]() ,设
,设![]() 。
。
(Ⅰ)证明:![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(Ⅱ)求点![]() 与平面
与平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小。
的大小。
解法一:
(Ⅰ)证明:∵平面![]() ∥平面
∥平面![]()
∴![]() ∥
∥![]()
∵![]()
∴![]()
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() 平面
平面![]()
 ∴
∴![]()
又∵![]()
∴![]() 为
为![]() 与
与![]() 的公垂线。
的公垂线。
(Ⅱ)过![]() 作
作![]() 于
于![]() ,
,
∵![]() 为正三角形,
为正三角形,
∴![]() 为
为![]() 中点,
中点,
∵![]() 平面
平面![]()
∴![]()
又∵![]()
∴![]() 平面
平面![]()
∴线段![]() 的长即为
的长即为![]() 到平面
到平面![]() 的距离
的距离
在等边三角形![]() 中,
中,![]()
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
(Ⅲ)过![]() 作
作![]() 于
于![]() ,连结
,连结![]()
由三垂线定理知![]()
∴![]() 是二面角
是二面角![]() 的平面角
的平面角
在![]() 中,
中,![]() ,
,![]() ~
~![]() ,
,![]()
 ∴
∴![]() ,∴
,∴![]()
所以,二面角![]() 的大小为
的大小为![]() 。
。
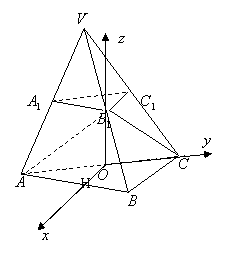
法二:取![]() 中点
中点![]() ,连结
,连结![]() ,易知
,易知![]() 平面
平面![]() ,
,
过![]() 作直线
作直线![]() ∥
∥![]() 交
交![]() 于
于![]()
取![]() 为空间直角坐标系的原点,
为空间直角坐标系的原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 如图建立空间直角坐标系,则
如图建立空间直角坐标系,则
![]()
![]()
(Ⅰ)![]()
∴![]()
∴![]() ,∴
,∴![]() ,
,
又∵![]() ∥
∥![]() ,由已知
,由已知![]() ,
,![]() ∥
∥![]()
∴![]() ,
,
即![]() 为
为![]() 与
与![]() 的公垂线。
的公垂线。
(Ⅱ)设![]() 是平面
是平面![]() 的一个法向量,又
的一个法向量,又![]() ,
,
则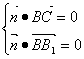 ,即
,即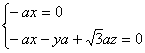 ,令
,令![]() ,则
,则![]()
∴![]()
设所求距离为![]() ,
,
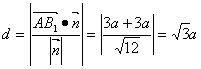
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
(Ⅲ)设平面![]() 的一个法向量为
的一个法向量为![]() ,又
,又![]()
则 则
则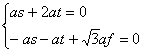 令
令![]() ,则
,则![]()
即![]() ,设二面角
,设二面角![]() 为
为![]() ,
,![]()
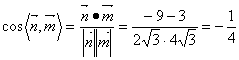
又二面角![]() 为锐角
为锐角
二面角![]() 的大小为
的大小为![]() 。
。
(21)(本小题满分12分)已知定点![]() ,动点
,动点![]() 满足条件:
满足条件:![]() ,点
,点![]() 的轨迹是曲线
的轨迹是曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点。如果
两点。如果![]() 。
。
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)若曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值。
的值。
解:(Ⅰ)∵![]()
∴点![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,![]() 的双曲线的左支,
的双曲线的左支,
∴曲线![]() 的方程为
的方程为![]()
设![]() ,把
,把![]() 代入
代入![]() 消去
消去![]() 得
得
![]()
∴![]()
∴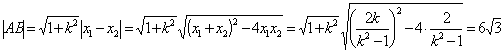
两边平方整理得![]() ,
,
∴![]() (∵
(∵![]() )
)
∴![]()
故直线方程为![]() 。
。
(Ⅱ)设![]() ,由已知
,由已知![]() ,得
,得![]()
∴![]()
∴![]()
∴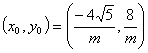
将点![]() 的坐标代入
的坐标代入![]() 得
得![]()
∴![]() 或
或![]() (舍去)。
(舍去)。
(22)(本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]()
(Ⅰ)写出![]() 与
与![]() 的递推关系式(
的递推关系式(![]() );
);
(Ⅱ)求![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
解法1:(Ⅰ)由![]() 及
及![]() 得
得
![]() 即
即![]()
∴![]()
(Ⅱ)由![]() 得
得
![]()
∴![]() 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
故![]()
∴![]()
(Ⅲ)∵![]()
∴![]()
∴![]()
∴![]() ………………①
………………①
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时
时![]() ………………②
………………②
由①-②得
![]() ;
;
∴![]()
综上得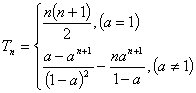 。
。
解法二、
(Ⅰ)由![]() 及
及![]() 得
得
![]()
![]()
猜测![]() 。用数学归纳法证明如下:
。用数学归纳法证明如下:
(1)![]() 时,
时,![]() 猜测成立;
猜测成立;
(2)假设![]() 时,命题成立,即
时,命题成立,即![]() ,则
,则
![]()
∴![]() ,即
,即![]() ,即
,即![]() 时命题也成立。
时命题也成立。
综合(1)、(2)知对于![]() 都有
都有![]()
所以![]() ,故
,故![]() 。
。
(Ⅱ)![]() ,证明见(Ⅰ)。
,证明见(Ⅰ)。