(数学选修2-3) 第一章 计数原理
[基础训练A组]
一、选择题
1![]() 将
将![]() 个不同的小球放入
个不同的小球放入![]() 个盒子中,则不同放法种数有( )
个盒子中,则不同放法种数有( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
2![]() 从
从![]() 台甲型和
台甲型和![]() 台乙型电视机中任意取出
台乙型电视机中任意取出![]() 台,其中至少有甲型与乙型电视机各
台,其中至少有甲型与乙型电视机各![]() 台,则不同的取法共有( )
台,则不同的取法共有( )
A![]()
![]() 种 B
种 B![]()
![]() 种 C
种 C![]()
![]() 种 D
种 D![]()
![]() 种
种
3![]()
![]() 个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有(
)
个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有(
)
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4![]()
![]() 共
共![]() 个人,从中选1名组长1名副组长,但
个人,从中选1名组长1名副组长,但![]() 不能当副组长,不同的选法总数是( )
不能当副组长,不同的选法总数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 现有男、女学生共
现有男、女学生共![]() 人,从男生中选
人,从男生中选![]() 人,从女生中选
人,从女生中选![]() 人分别参加数学、物理、化学三科竞赛,共有
人分别参加数学、物理、化学三科竞赛,共有![]() 种不同方案,那么男、女生人数分别是( )
种不同方案,那么男、女生人数分别是( )
A![]() 男生
男生![]() 人,女生
人,女生![]() 人
B
人
B![]() 男生
男生![]() 人,女生
人,女生![]() 人
人
C![]() 男生
男生![]() 人,女生
人,女生![]() 人
D
人
D![]() 男生
男生![]() 人,女生
人,女生![]() 人
人![]()
6![]() 在
在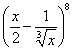 的展开式中的常数项是( )
的展开式中的常数项是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
7![]()
![]() 的展开式中
的展开式中![]() 的项的系数是( )
的项的系数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
8![]()
![]() 展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
1![]() 从甲、乙,……,等
从甲、乙,……,等![]() 人中选出
人中选出![]() 名代表,那么(1)甲一定当选,共有
种选法
名代表,那么(1)甲一定当选,共有
种选法![]() (2)甲一定不入选,共有 种选法
(2)甲一定不入选,共有 种选法![]() (3)甲、乙二人至少有一人当选,共有 种选法
(3)甲、乙二人至少有一人当选,共有 种选法![]()
2![]()
![]() 名男生,
名男生,![]() 名女生排成一排,女生不排两端,则有 种不同排法
名女生排成一排,女生不排两端,则有 种不同排法![]()
3![]() 由
由![]() 这六个数字组成_____个没有重复数字的六位奇数
这六个数字组成_____个没有重复数字的六位奇数![]()
4![]() 在
在![]() 的展开式中,
的展开式中,![]() 的系数是
的系数是 ![]()
5![]() 在
在![]() 展开式中,如果第
展开式中,如果第![]() 项和第
项和第![]() 项的二项式系数相等,
项的二项式系数相等,
则![]() ,
,![]()
![]()
6![]() 在
在![]() 的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
7![]() 用
用![]() 四个不同数字组成四位数,所有这些四位数中的数字的总和为
四个不同数字组成四位数,所有这些四位数中的数字的总和为![]() ,则
,则![]()
![]()
8![]() 从
从![]() 中任取三个数字,从
中任取三个数字,从![]() 中任取两个数字,组成没有重复数字的五位数,共有________________个?
中任取两个数字,组成没有重复数字的五位数,共有________________个?
三、解答题
1![]() 判断下列问题是排列问题还是组合问题?并计算出结果
判断下列问题是排列问题还是组合问题?并计算出结果![]()
(1)高三年级学生会有![]() 人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手?
人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手?
(2)高二年级数学课外小组![]() 人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选
人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选![]() 名参加省数学竞赛,有多少种不同的选法?
名参加省数学竞赛,有多少种不同的选法?
(3)有![]() 八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
2![]()
![]() 个排成一排,在下列情况下,各有多少种不同排法?
个排成一排,在下列情况下,各有多少种不同排法?
(1)甲排头,
(2)甲不排头,也不排尾,
(3)甲、乙、丙三人必须在一起,
(4)甲、乙之间有且只有两人,
(5)甲、乙、丙三人两两不相邻,
(6)甲在乙的左边(不一定相邻),
(7)甲、乙、丙三人按从高到矮,自左向右的顺序,
(8)甲不排头,乙不排当中![]()
3![]() 解方程
解方程![]()
![]()
4![]() 已知
已知![]() 展开式中的二项式系数的和比
展开式中的二项式系数的和比![]() 展开式的二项式系数的和大
展开式的二项式系数的和大![]() ,求
,求![]() 展开式中的系数最大的项和系数量小的项
展开式中的系数最大的项和系数量小的项![]()
5![]() (1)在
(1)在![]() 的展开式中,若第
的展开式中,若第![]() 项与第
项与第![]() 项系数相等,且
项系数相等,且![]() 等于多少?
等于多少?
(2)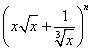 的展开式奇数项的二项式系数之和为
的展开式奇数项的二项式系数之和为![]() ,
,
则求展开式中二项式系数最大的项![]()
6![]() 已知
已知![]() 其中
其中![]() 是常数,计算
是常数,计算![]()
(数学选修2-3) 第一章 计数原理
参考答案
[基础训练A组]
一、选择题
1![]() B 每个小球都有
B 每个小球都有![]() 种可能的放法,即
种可能的放法,即![]()
2![]() C 分两类:(1)甲型
C 分两类:(1)甲型![]() 台,乙型
台,乙型![]() 台:
台:![]() ;(2)甲型
;(2)甲型![]() 台,乙型
台,乙型![]() 台:
台:![]()
![]()
3![]() C 不考虑限制条件有
C 不考虑限制条件有![]() ,若甲,乙两人都站中间有
,若甲,乙两人都站中间有![]() ,
,![]() 为所求
为所求
4![]() B 不考虑限制条件有
B 不考虑限制条件有![]() ,若
,若![]() 偏偏要当副组长有
偏偏要当副组长有![]() ,
,![]() 为所求
为所求
5![]() B 设男学生有
B 设男学生有![]() 人,则女学生有
人,则女学生有![]() 人,则
人,则![]()
即![]()
6![]() A
A ![]()
令![]()
7![]() B
B ![]()
![]()
8![]() A 只有第六项二项式系数最大,则
A 只有第六项二项式系数最大,则![]() ,
,
![]() ,令
,令![]()
二、填空题
1![]() (1)
(1)![]()
![]() ;(2)
;(2) ![]()
![]() ;(3)
;(3)![]()
![]()
2![]()
![]() 先排女生有
先排女生有![]() ,再排男生有
,再排男生有![]() ,共有
,共有![]()
3![]()
![]()
![]() 既不能排首位,也不能排在末尾,即有
既不能排首位,也不能排在末尾,即有![]() ,其余的有
,其余的有![]() ,共有
,共有![]()
4![]()
![]()
![]() ,令
,令![]()
5![]()
![]()
![]()
6![]()
![]() 先排首末,从五个奇数中任取两个来排列有
先排首末,从五个奇数中任取两个来排列有![]() ,其余的
,其余的![]() ,共有
,共有![]()
7![]()
![]() 当
当![]() 时,有
时,有![]() 个四位数,每个四位数的数字之和为
个四位数,每个四位数的数字之和为![]()
![]() ;当
;当![]() 时,
时,![]() 不能被
不能被![]() 整除,即无解
整除,即无解
8![]()
![]() 不考虑
不考虑![]() 的特殊情况,有
的特殊情况,有![]() 若
若![]() 在首位,则
在首位,则![]()
![]()
三、解答题
1![]() 解:(1)①是排列问题,共通了
解:(1)①是排列问题,共通了![]() 封信;②是组合问题,共握手
封信;②是组合问题,共握手![]() 次
次![]()
(2)①是排列问题,共有![]() 种选法;②是组合问题,共有
种选法;②是组合问题,共有![]() 种选法
种选法![]()
(3)①是排列问题,共有![]() 个商;②是组合问题,共有
个商;②是组合问题,共有![]() 个积
个积![]()
2![]() 解:(1)甲固定不动,其余有
解:(1)甲固定不动,其余有![]() ,即共有
,即共有![]() 种;
种;
(2)甲有中间![]() 个位置供选择,有
个位置供选择,有![]() ,其余有
,其余有![]() ,即共有
,即共有![]() 种;
种;
(3)先排甲、乙、丙三人,有![]() ,再把该三人当成一个整体,再加上另四人,相当于
,再把该三人当成一个整体,再加上另四人,相当于![]() 人的全排列,即
人的全排列,即![]() ,则共有
,则共有![]() 种;
种;
(4)从甲、乙之外的![]() 人中选
人中选![]() 个人排甲、乙之间,有
个人排甲、乙之间,有![]() ,甲、乙可以交换有
,甲、乙可以交换有![]() ,
,
把该四人当成一个整体,再加上另三人,相当于![]() 人的全排列,
人的全排列,
则共有![]() 种;
种;
(5)先排甲、乙、丙之外的四人,有![]() ,四人形成五个空位,甲、乙、丙三人排
,四人形成五个空位,甲、乙、丙三人排
这五个空位,有![]() ,则共有
,则共有![]() 种;
种;
(6)不考虑限制条件有![]() ,甲在乙的左边(不一定相邻),占总数的一半,
,甲在乙的左边(不一定相邻),占总数的一半,
即![]() 种;
种;
(7)先在![]() 个位置上排甲、乙、丙之外的四人,有
个位置上排甲、乙、丙之外的四人,有![]() ,留下三个空位,甲、乙、丙三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即
,留下三个空位,甲、乙、丙三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即![]()
(8)不考虑限制条件有![]() ,而甲排头有
,而甲排头有![]() ,乙排当中有
,乙排当中有![]() ,这样重复了甲排头,乙排当中
,这样重复了甲排头,乙排当中![]() 一次,即
一次,即![]()
3![]() 解:
解: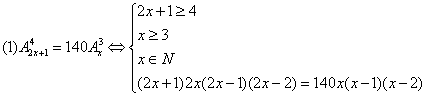
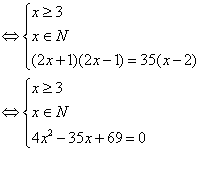
得![]()
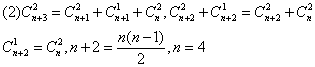
4![]() 解:
解:![]() ,
,![]() 的通项
的通项![]()
当![]() 时,展开式中的系数最大,即
时,展开式中的系数最大,即![]() 为展开式中的系数最大的项;
为展开式中的系数最大的项;
当![]() 时,展开式中的系数最小,即
时,展开式中的系数最小,即![]() 为展开式中
为展开式中
的系数最小的项![]()
5![]() 解:(1)由已知得
解:(1)由已知得![]()
(2)由已知得![]() ,而展开式中二项式
,而展开式中二项式
系数最大项是![]()
![]()
6![]() 解:设
解:设![]() ,令
,令![]() ,得
,得![]()
令![]() ,得
,得![]()
![]()
![]()