(数学选修2-3) 第一章 计数原理
[提高训练C组]
一、选择题
1![]() 若
若![]() ,则
,则![]() 的值为( )
的值为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
2![]() 某班有
某班有![]() 名男生,
名男生,![]() 名女生,现要从中选出
名女生,现要从中选出![]() 人组成一个宣传小组,
人组成一个宣传小组,
其中男、女学生均不少于![]() 人的选法为( )
人的选法为( )
A![]()
![]()
![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
3![]()
![]() 本不同的书分给甲、乙、丙三人,每人两本,不同的分法种数是( )
本不同的书分给甲、乙、丙三人,每人两本,不同的分法种数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4![]() 设含有
设含有![]() 个元素的集合的全部子集数为
个元素的集合的全部子集数为![]() ,其中由
,其中由![]() 个元素组成的子集数为
个元素组成的子集数为![]() ,则
,则![]() 的值为( )
的值为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 若
若![]() ,则
,则![]() 的值为( )
的值为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
6![]() 在
在![]() 的展开式中,若第七项系数最大,则
的展开式中,若第七项系数最大,则![]() 的值可能等于( )
的值可能等于( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
7![]() 不共面的四个定点到平面
不共面的四个定点到平面![]() 的距离都相等,这样的平面
的距离都相等,这样的平面![]() 共有( )
共有( )
A![]()
![]() 个 B
个 B![]()
![]() 个
个
C![]()
![]() 个 D
个 D![]()
![]() 个
个
8![]() 由
由![]() 十个数码和一个虚数单位
十个数码和一个虚数单位![]() 可以组成虚数的个数为( )
可以组成虚数的个数为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
1![]() 将数字
将数字![]() 填入标号为
填入标号为![]() 的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不同的填法有 种?
的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不同的填法有 种?
2![]() 在△
在△![]() 的边
的边![]() 上有
上有![]() 个点,边
个点,边![]() 上有
上有![]() 个点,加上
个点,加上![]() 点共个点,以这
点共个点,以这![]() 个点为顶点的三角形有 个
个点为顶点的三角形有 个![]()
3![]() 从
从![]() ,
,![]() 这七个数字中任取三个不同数字作为二次函数
这七个数字中任取三个不同数字作为二次函数![]() 的系数
的系数![]() 则可组成不同的函数_______个,其中以
则可组成不同的函数_______个,其中以![]() 轴作为该函数的图像的对称轴的函数有______个
轴作为该函数的图像的对称轴的函数有______个![]()
4![]() 若
若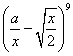 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,则常数
,则常数![]() 的值为
的值为 ![]()
5![]() 若
若![]() 则自然数
则自然数![]() _____
_____![]()
6![]() 若
若![]() ,则
,则![]()
![]()
7![]()
![]() 的近似值(精确到
的近似值(精确到![]() )是多少?
)是多少?
8![]() 已知
已知![]() ,那么
,那么![]() 等于多少?
等于多少?
三、解答题
1![]()
![]() 个人坐在一排
个人坐在一排![]() 个座位上,问(1)空位不相邻的坐法有多少种?(2)
个座位上,问(1)空位不相邻的坐法有多少种?(2) ![]() 个空位只有
个空位只有![]() 个相邻的坐法有多少种?(3)
个相邻的坐法有多少种?(3) ![]() 个空位至多有
个空位至多有![]() 个相邻的坐法有多少种?
个相邻的坐法有多少种?
2![]() 有
有![]() 个球,其中
个球,其中![]() 个黑球,红、白、蓝球各
个黑球,红、白、蓝球各![]() 个,现从中取出
个,现从中取出![]() 个球排成一列,共有多少种不同的排法?
个球排成一列,共有多少种不同的排法?
3![]() 求
求![]() 展开式中按
展开式中按![]() 的降幂排列的前两项
的降幂排列的前两项![]()
4![]() 用二项式定理证明:
用二项式定理证明:![]() 能被
能被![]() 整除
整除![]()
![]()
5![]() 求证:
求证:![]()
![]()
6![]() (1)若
(1)若![]() 的展开式中,
的展开式中,![]() 的系数是
的系数是![]() 的系数的
的系数的![]() 倍,求
倍,求![]() ;
;
(2)已知![]() 的展开式中,
的展开式中, ![]() 的系数是
的系数是![]() 的系数与
的系数与![]() 的系数的等差中项,求
的系数的等差中项,求![]() ;
;
(3)已知![]() 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于![]() ,求
,求![]()
![]()
(数学选修2-3) 第一章 计数原理
参考答案
[提高训练C组]
一、选择题
1![]() B
B ![]()
2![]() D 男生
D 男生![]() 人,女生
人,女生![]() 人,有
人,有![]() ;男生
;男生![]() 人,女生
人,女生![]() 人,有
人,有![]()
共计![]()
3![]() A 甲得
A 甲得![]() 本有
本有![]() ,乙从余下的
,乙从余下的![]() 本中取
本中取![]() 本有
本有![]() ,余下的
,余下的![]() ,共计
,共计![]()
4![]() B 含有
B 含有![]() 个元素的集合的全部子集数为
个元素的集合的全部子集数为![]() ,由
,由![]() 个元素组成的子集数
个元素组成的子集数
为![]() ,
,![]()
5![]() A
A ![]()
![]()
6![]() D 分三种情况:(1)若仅
D 分三种情况:(1)若仅![]() 系数最大,则共有
系数最大,则共有![]() 项,
项,![]() ;(2)若
;(2)若![]() 与
与![]() 系数相等且最大,则共有
系数相等且最大,则共有![]() 项,
项,![]() ;(3)若
;(3)若![]() 与
与![]() 系数相等且最大,则共有
系数相等且最大,则共有![]() 项,
项,![]() ,所以
,所以![]() 的值可能等于
的值可能等于![]()
7![]() D 四个点分两类:(1)三个与一个,有
D 四个点分两类:(1)三个与一个,有![]() ;(2)平均分二个与二个,有
;(2)平均分二个与二个,有![]()
共计有![]()
8![]() D 复数
D 复数![]() 为虚数,则
为虚数,则![]() 有
有![]() 种可能,
种可能,![]() 有
有![]() 种可能,共计
种可能,共计![]() 种可能
种可能
二、填空题
1![]()
![]() 分三类:第一格填
分三类:第一格填![]() ,则第二格有
,则第二格有![]() ,第三、四格自动对号入座,不能自由排列;
,第三、四格自动对号入座,不能自由排列;
第一格填![]() ,则第三格有
,则第三格有![]() ,第一、四格自动对号入座,不能自由排列;
,第一、四格自动对号入座,不能自由排列;
第一格填![]() ,则第撕格有
,则第撕格有![]() ,第二、三格自动对号入座,不能自由排列;
,第二、三格自动对号入座,不能自由排列;
共计有![]()
2![]()
![]()
![]()
3![]()
![]()
![]() ,
,![]() ;
;![]()
4![]()
![]()
![]() ,令
,令![]()
![]()
5![]()
![]()
![]()
![]()
6![]()
![]()
![]()
而![]() ,得
,得![]()
7![]()
![]()
![]()
8![]()
![]() 设
设![]() ,令
,令![]() ,得
,得![]()
令![]() ,得
,得![]() ,
,![]()
三、解答题
1![]() 解:
解:![]() 个人排有
个人排有![]() 种,
种, ![]() 人排好后包括两端共有
人排好后包括两端共有![]() 个“间隔”可以插入空位
个“间隔”可以插入空位![]()
(1)空位不相邻相当于将![]() 个空位安插在上述
个空位安插在上述![]() 个“间隔”中,有
个“间隔”中,有![]() 种插法,
种插法,
故空位不相邻的坐法有![]() 种
种![]()
(2)将相邻的![]() 个空位当作一个元素,另一空位当作另一个元素,往
个空位当作一个元素,另一空位当作另一个元素,往![]() 个“间隔”里插
个“间隔”里插
有![]() 种插法,故
种插法,故![]() 个空位中只有
个空位中只有![]() 个相邻的坐法有
个相邻的坐法有![]() 种
种![]()
(3) ![]() 个空位至少有
个空位至少有![]() 个相邻的情况有三类:
个相邻的情况有三类:
①![]() 个空位各不相邻有
个空位各不相邻有![]() 种坐法;
种坐法;
②![]() 个空位
个空位![]() 个相邻,另有
个相邻,另有![]() 个不相邻有
个不相邻有![]() 种坐法;
种坐法;
③![]() 个空位分两组,每组都有
个空位分两组,每组都有![]() 个相邻,有
个相邻,有![]() 种坐法
种坐法![]()
综合上述,应有![]() 种坐法
种坐法![]()
2![]() 解:分三类:若取
解:分三类:若取![]() 个黑球,和另三个球,排
个黑球,和另三个球,排![]() 个位置,有
个位置,有![]() ;
;
若取![]() 个黑球,从另三个球中选
个黑球,从另三个球中选![]() 个排
个排![]() 个位置,
个位置,![]() 个黑球是相同的,
个黑球是相同的,
自动进入,不需要排列,即有![]() ;
;
若取![]() 个黑球,从另三个球中选
个黑球,从另三个球中选![]() 个排
个排![]() 个位置,
个位置,![]() 个黑球是相同的,
个黑球是相同的,
自动进入,不需要排列,即有![]() ;
;
所以有![]() 种
种![]()
3![]() 解:
解:![]()
![]()
![]()
![]()
4![]() 解:
解:![]()
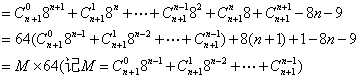
![]() ,
,![]()
5![]() 证明:
证明:![]()
![]()
![]()
6![]() 解:(1)
解:(1)![]() ;
;
(2)![]()
得![]() ;
;
(3)![]()
得![]() ,或
,或![]()
所以![]()
![]()