(数学选修2-3) 第一章 计数原理
[综合训练B组]
一、选择题
1![]() 由数字
由数字![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成没有重复数字的五位数,其中小于
组成没有重复数字的五位数,其中小于![]() 的偶数共有( )
的偶数共有( )
A![]()
![]() 个 B
个 B![]()
![]() 个 C
个 C![]()
![]() 个 D
个 D![]()
![]() 个
个
2![]()
![]() 张不同的电影票全部分给
张不同的电影票全部分给![]() 个人,每人至多一张,则有不同分法的种数是( )
个人,每人至多一张,则有不同分法的种数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
3![]()
![]() 且
且![]() ,则乘积
,则乘积![]() 等于
等于
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4![]() 从字母
从字母![]() 中选出4个数字排成一列,其中一定要选出
中选出4个数字排成一列,其中一定要选出![]() 和
和![]() ,并且必须相邻(
,并且必须相邻(![]() 在
在![]() 的前面),共有排列方法( )种
的前面),共有排列方法( )种![]()
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 从不同号码的
从不同号码的![]() 双鞋中任取
双鞋中任取![]() 只,其中恰好有
只,其中恰好有![]() 双的取法种数为( )
双的取法种数为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
6![]() 把
把![]() 按照二项式定理来展开,则展开式的第
按照二项式定理来展开,则展开式的第![]() 项的系数是( )
项的系数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
7![]() 在
在![]() 的展开式中,
的展开式中,![]() 的系数是
的系数是![]() ,则
,则![]() 的系数是( )
的系数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
8![]() 在
在![]() 的展开中,
的展开中,![]() 的系数是( )
的系数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
1![]()
![]() 个人参加某项资格考试,能否通过,有 种可能的结果?
个人参加某项资格考试,能否通过,有 种可能的结果?
2![]() 以
以![]() 这几个数中任取
这几个数中任取![]() 个数,使它们的和为奇数,则共有 种不同取法
个数,使它们的和为奇数,则共有 种不同取法![]()
3![]() 已知集合
已知集合![]() ,
,![]() ,从集合
,从集合![]() ,
,![]() 中各取一个元素作为点的坐标,可作出不同的点共有_____个
中各取一个元素作为点的坐标,可作出不同的点共有_____个![]()
4![]()
![]() 且
且![]() 若
若![]() 则
则![]() ______
______![]()
5![]()
![]() 展开式中的常数项有
展开式中的常数项有
6![]() 在
在![]() 件产品
件产品![]() 中有
中有![]() 件是次品,从中任意抽了
件是次品,从中任意抽了![]() 件,至少有
件,至少有![]() 件是次品的抽法共有______________种(用数字作答)
件是次品的抽法共有______________种(用数字作答)![]()
7![]()
![]() 的展开式中的
的展开式中的![]() 的系数是___________
的系数是___________
8![]()
![]() ,则含有五个元素,且其中至少有两个偶数的子集个数为_____
,则含有五个元素,且其中至少有两个偶数的子集个数为_____![]()
三、解答题
1![]() 集合
集合![]() 中有
中有![]() 个元素,集合
个元素,集合![]() 中有
中有![]() 个元素,集合
个元素,集合![]()
![]()
![]() 中有
中有![]() 个元素,集合
个元素,集合![]() 满足
满足
(1)![]() 有
有![]() 个元素; (2)
个元素; (2)![]()
![]()
![]()
![]()
![]()
(3)![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() 求这样的集合
求这样的集合![]() 的集合个数
的集合个数![]()
2![]() 计算:(1)
计算:(1)![]() ;
;
(2)![]()
![]()
(3)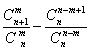
3![]() 证明:
证明:![]()
![]()
4![]() 求
求![]() 展开式中的常数项
展开式中的常数项![]()
5![]() 从
从![]() 中任选三个不同元素作为二次函数
中任选三个不同元素作为二次函数![]() 的系数,问能组成多少条图像为经过原点且顶点在第一象限或第三象限的抛物线?
的系数,问能组成多少条图像为经过原点且顶点在第一象限或第三象限的抛物线?
6![]()
![]() 张椅子排成,有
张椅子排成,有![]() 个人就座,每人
个人就座,每人![]() 个座位,恰有
个座位,恰有![]() 个连续空位的坐法共有多少种?
个连续空位的坐法共有多少种?
(数学选修2-3) 第一章 计数原理
参考答案
[综合训练B组]
一、选择题
1![]() C 个位
C 个位![]() ,万位
,万位![]() ,其余
,其余![]() ,共计
,共计![]()
2![]() D 相当于
D 相当于![]() 个元素排
个元素排![]() 个位置,
个位置,![]()
3![]() B 从
B 从![]() 到
到![]() 共计有
共计有![]() 个正整数,即
个正整数,即![]()
4![]() A 从
A 从![]() 中选
中选![]() 个,有
个,有![]() ,把
,把![]() 看成一个整体,则
看成一个整体,则![]() 个元素全排列,
个元素全排列,![]()
共计![]()
5![]() A 先从
A 先从![]() 双鞋中任取
双鞋中任取![]() 双,有
双,有![]() ,再从
,再从![]() 只鞋中任取
只鞋中任取![]() 只,即
只,即![]() ,但需要排除
,但需要排除
![]() 种成双的情况,即
种成双的情况,即![]() ,则共计
,则共计![]()
6![]() D
D ![]() ,系数为
,系数为![]()
7![]() A
A ![]() ,令
,令![]()
则![]() ,再令
,再令![]()
8![]() D
D ![]()
二、填空题
1![]()
![]() 每个人都有通过或不通过
每个人都有通过或不通过![]() 种可能,共计有
种可能,共计有![]()
2![]()
![]() 四个整数和为奇数分两类:一奇三偶或三奇一偶,即
四个整数和为奇数分两类:一奇三偶或三奇一偶,即![]()
3![]()
![]()
![]() ,其中
,其中![]() 重复了一次
重复了一次
4![]()
![]()
![]()
5![]()
![]()
![]() 的通项为
的通项为![]() 其中
其中![]() 的通项为
的通项为
![]() ,所以通项为
,所以通项为![]() ,令
,令![]()
得![]() ,当
,当![]() 时,
时,![]() ,得常数为
,得常数为![]() ;当
;当![]() 时,
时,![]() ,得常数为
,得常数为![]() ;
;
当![]() 时,
时,![]() ,得常数为
,得常数为![]() ;
;![]()
6![]()
![]()
![]() 件次品,或
件次品,或![]() 件次品,
件次品,![]()
7![]()
![]() 原式
原式![]() ,
,![]() 中含有
中含有![]() 的项是
的项是
![]() ,所以展开式中的
,所以展开式中的![]() 的系数是
的系数是![]()
8![]()
![]() 直接法:分三类,在
直接法:分三类,在![]() 个偶数中分别选
个偶数中分别选![]() 个,
个,![]() 个,
个,![]() 个偶数,其余选奇数,
个偶数,其余选奇数,
![]() ;间接法:
;间接法:![]()
三、解答题
1![]() 解:
解:![]() 中有元素
中有元素![]()
![]()
![]()
2![]() 解:(1)原式
解:(1)原式![]()
![]()
(2)原式![]()
![]()
另一方法: ![]()
![]()
(3)原式![]()
3![]() 证明:左边
证明:左边![]()
![]() 右边
右边
所以等式成立![]()
4![]() 解:
解: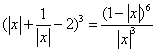 ,在
,在![]() 中,
中,![]() 的系数
的系数![]()
就是展开式中的常数项![]()
另一方法: 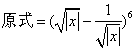 ,
,![]()
5![]() 解:抛物线经过原点,得
解:抛物线经过原点,得![]() ,
,
当顶点在第一象限时,![]() ,则有
,则有![]() 种;
种;
当顶点在第三象限时,![]() ,则有
,则有![]() 种;
种;
共计有![]() 种
种![]()
6![]() 解:把
解:把![]() 个人先排,有
个人先排,有![]() ,且形成了
,且形成了![]() 个缝隙位置,再把连续的
个缝隙位置,再把连续的![]() 个空位和
个空位和![]() 个空位
个空位
当成两个不同的元素去排![]() 个缝隙位置,有
个缝隙位置,有![]() ,所以共计有
,所以共计有![]() 种
种![]()