九、直线、平面、简单几何体
考试要求:1、掌握平面的基本性质,会用斜二侧的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。2、掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念,掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理。3、理解空间向量的概念,掌握空间向量的加法、减法和数乘。4、了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算。5、掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式。6、理解直线的方向向量,平面的法向量、向量在平面内的射影等概念。7、掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念。对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离。掌握直线和平面垂直的性质定理。掌握两个平面平行、垂直的判定定理和性质定理。8、了解多面体、凸多面体的概念,了解正多面体的概念。9、了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。10、了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。
11、了解球的概念,掌握球的性质,掌握球的表面积、体积公式。
1、已知直线m,n,平面![]() ,给出下列命题:
,给出下列命题:
①若![]() ;②若
;②若![]() ;③若
;③若![]() ;
;
④若异面直线m,n互相垂直,则存在过m的平面与n垂直.其中正确的命题是:
A.②③ B.①③ C.②④ D.③④
2、已知平面α、β、γ,直线l、m,且![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则其中正确的个数是:
.则其中正确的个数是:
|
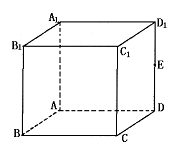
3、如图,点E是正方体ABCD—A1B1C1D1的棱DD1
的中点,则过点E且与直线AB、B1C1都相交的
直线的条数是:
A.0 B.1
C.2 D.无数条
4、已知四个命题:
①若直线l∥平面![]() ,则直线l的垂线必平行于平面
,则直线l的垂线必平行于平面![]() ;
;
②若直线l与平面![]() 相交,则有且只有一个平面经过l与平面
相交,则有且只有一个平面经过l与平面![]() 垂直;
垂直;
③若一个三棱锥每两个相邻侧面所成的角都相等,则这个三棱锥是正三棱锥;
④若四棱住的任意两条对角线都相交且互相平分,则这个四棱柱为平行六面体.
其中正确的命题是:
A.① B.② C.③ D.④
5、在正三棱锥S—ABC中,侧棱SC⊥侧面SAB,侧棱SC=![]() ,则此正三棱锥的外接球的表面积为
,则此正三棱锥的外接球的表面积为
6、在空间中,下列命题中正确的是:
①若两直线a、b分别与直线l平行,则a//b
②若直线a与平面β内的一条直线b平行,则a//β
③若直线a与平面β内的两条直线都垂直,则a⊥β
④若平面β内的一条直线a垂直平面γ,则β⊥γ
A.①②④ B.①④ C.①③④ D.①②③④
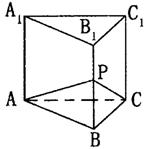
|
把棱柱分成两部分的体积之比为5∶1,则二面角P—AC—B
的大小为 :
A.30° B.45°
C.60° D.75°
8、球面上有A、B、C三点,其中任意两点的球面距离都等于大圆周长的![]() ,过A、B、C
,过A、B、C
的小圆圆心到△ABC的边BC的距离为1,那么球的面积为
9、P是正三棱柱ABC—A1B1C1的侧棱CC1上一点(侧棱端点除外),则∠APB的大小满足:
A.![]() B.
B.![]()
C.![]() D.以上都有可能
D.以上都有可能
10、锥体体积V可以由底面积S与高h求得:![]() . 已知正三棱锥P—ABC底面边长为2
. 已知正三棱锥P—ABC底面边长为2![]() ,体积为4
,体积为4![]() ,则底面三角形ABC的中心O到侧面PAB的距离为 .
,则底面三角形ABC的中心O到侧面PAB的距离为 .
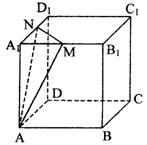
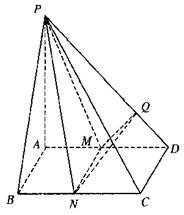
|
M、N分别是棱A1B1、A1D1的中点,则点B到平
面AMN的距离是 ( )
A.![]() B.
B.![]()
|
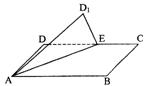
12、如图,矩形ABCD中,DC=![]() ,AD=1,在DC上截取DE=1,
,AD=1,在DC上截取DE=1,
将△ADE沿AE翻折到D1点,点D1在平面ABC上的射影落在
AC上时,二面角D1—AE—B的平面角的余弦值是 .
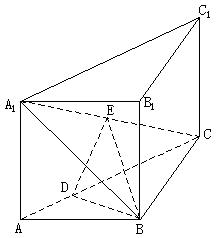 13、如图:直三棱柱ABC-A1B1C1中,
13、如图:直三棱柱ABC-A1B1C1中,![]() ,E是A1C的中点,
,E是A1C的中点,![]() 且交AC于D,
且交AC于D,![]() 。
。
(I)证明:![]() 平面
平面![]() ;
;
(II)证明:![]() 平面
平面![]() ;
;
(III)求平面![]() 与平面EDB所成的二面角
与平面EDB所成的二面角
的大小(仅考虑平面角为锐角的情况)。
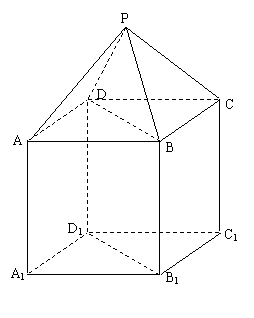 14、如图,P—ABCD是正四棱锥,
14、如图,P—ABCD是正四棱锥,![]()
是正方体,其中![]() 。
。
(1)求证:![]() ;
;
(2)求平面PAD与平面![]() 所成的锐二面角
所成的锐二面角![]() 的
的
大小。
 15、如图,已知正四棱锥
15、如图,已知正四棱锥![]() —
—![]() 的底面边长为4,高为6,点
的底面边长为4,高为6,点![]() 是高的中点,点
是高的中点,点![]() 是侧面
是侧面![]() 的重心.求:
的重心.求:
(1)![]() 、
、![]() 两点间的距离;
两点间的距离;
(2)异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)直线![]() 与底面
与底面![]() 所成的角.
所成的角.
16、矩形ABCD中,![]() ,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
(I)求证:PD⊥PC;
(II)求二面角P—DB—C的大小;
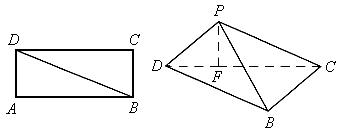 (III)求直线CD与平面PBD所成角的大小。
(III)求直线CD与平面PBD所成角的大小。
|
(Ⅰ)求证:平面PMN⊥平面PAD;
(Ⅱ)求PA的长;
(Ⅲ)求二面角P—MN—Q的余弦值.
 18、如图:已知在
18、如图:已知在![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求直线![]() 和
和![]() 所成的角;
所成的角;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)若![]() 是线段
是线段![]() 上的一个动点,请确定点
上的一个动点,请确定点![]() 的
的
位置,使得平面![]() 平面
平面![]() .
.
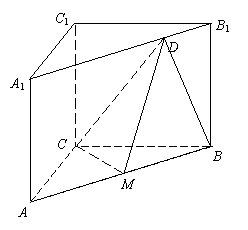 19、如图,在直三棱柱
19、如图,在直三棱柱![]() 中,
中,![]() ,
,
![]() ,
,![]() 为
为![]() 的中点,D在A1B1上
的中点,D在A1B1上
且![]() .
.
(I)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的大小.
的大小.
九、直线、平面、简单几何体参考答案
1、D;2、C;3、B;4、D;5、![]() ;6、B;7、A;8、
;6、B;7、A;8、![]() ;9、D;10、
;9、D;10、![]() ;
;
11、D;12、![]()
13. (I)证:![]() 三棱柱
三棱柱![]() 中
中![]() , 又
, 又![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,![]() 平面
平面![]()
(II)证:![]() 三棱柱
三棱柱![]() 中
中![]() ,
,![]() 中
中![]()
![]() 是等腰三角形,
是等腰三角形,
![]() E是等腰
E是等腰![]() 底边
底边![]() 的中点,
的中点,![]()
又依条件知![]() ,且
,且![]()
由①,②,③得![]() 平面EDB
平面EDB
(III)解:![]() 平面
平面![]() ,且
,且![]() 不平行,
不平行,
故延长![]() ,ED后必相交,设交点为E,连接EF,如下图
,ED后必相交,设交点为E,连接EF,如下图
![]() 是所求的二面角,依条件易证明
是所求的二面角,依条件易证明![]()
![]() 为
为![]() 中点,
中点,![]() A为
A为![]() 中点,
中点,![]()
![]() ,
,![]() , 即
, 即![]()
又![]() 平面EFB,
平面EFB,![]() ,
,![]() 是所求的二面角的平面角
是所求的二面角的平面角
![]() E为等腰直角三角形
E为等腰直角三角形![]() 底边中点,
底边中点,![]()
故所求的二面角的大小为![]()
14、解: 以A1B1所在直线为轴,A1D1所在直线为y轴,A1A所在直线为z轴,建立空间直角坐标系。
(1)设E是BD的中点,∵P-ABCD是正四棱锥,![]() ,
,
又![]() ,
, ![]() ,
, ![]() ,
,
∴ = (-2,2,0), = (1,1,2),
∵ ·=0,∴ ⊥,即![]() 。
。
(2)设平面PAD的法向量是m = (x,y,z), ∵= (0,2,0) , = (1,1,2) ,
∴ Þ Þ ,
取![]() 得m = (-2,0,1),∴cos<m,n> = = - ,
得m = (-2,0,1),∴cos<m,n> = = - ,
![]() 。
。
15.解:如图所示,建立空间直角坐标系,![]() 是底面的中心,
是底面的中心,![]() ∥
∥![]() ,
,![]() ∥
∥![]() .
.
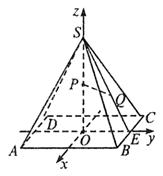 则有关点的坐标为
则有关点的坐标为![]() ,
,![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的重心,
的重心,
∴它们的坐标为![]() ,
,![]() .
.
(1)![]() .
.
∴![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
(2)![]() ,
,![]() ,设
,设![]() 、
、![]() 的夹角为
的夹角为![]() ,
,![]()
![]() ,
,
∴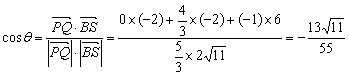 .
.
∴异面直线![]() 、
、![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)![]() 是
是![]() 的中点,可以证明直线
的中点,可以证明直线![]() 是直线
是直线![]() 在平面
在平面![]() 上的射影.
上的射影.
故![]() 与
与![]() 所成角就是
所成角就是![]() 与平面
与平面![]() 所成的角.点
所成的角.点![]() 的坐标为(0,2,0)
的坐标为(0,2,0)
∴![]() =(0,2,0),
=(0,2,0),![]() =(0,
=(0,![]() ,-1).
,-1).
设![]() 、
、![]() 的夹角为
的夹角为![]() ,则
,则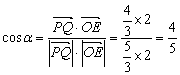 .
.
∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
16、(I)证明:∵四边形ABCD为矩形,∴BC⊥CD,DA⊥AB,∵A点移动到了P点
∴PD⊥PB,又∵P点在平面BCD上的射影在CD上,∴过P点作PF⊥CD
∴PF⊥面BCD,∴BC⊥面PCD,∴BC⊥PD,∴PD⊥面PBC, ∴PD⊥PC
(II)解:∵PF⊥面BCD, ∴过点F作FE⊥BD,连结PE
∴∠PEF为二面角P—BD—C的平面角,∵PD⊥PC,∴△CPD为Rt△
![]() ,
,![]()
又∵在![]() 中,
中,![]() ,∴PE=3
,∴PE=3
![]() ,
,![]()
(III)解:过F点作FG⊥PE,由(2)可知FG⊥面PBD,连结GD
∴∠GDF为直线CD与平面PDB所成的角
∵在![]() 中,
中,![]() ,∴DF=2
,∴DF=2
∵在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
, ![]()
17、解:(I)以A为坐标原点,分别以AB,AD,AP所在的直线为x轴,y轴和z轴,建立空间直角坐标系(图略).
设PA=a,则A(0,0,0),B(2,0,0)C(2,2,0),D(0,2,0)P(0,0,a),
M(0,1,0),N(2,1,0).![]()
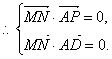 ∴MN⊥平面PAD. ∵MN
∴MN⊥平面PAD. ∵MN![]() 平面PMN,∴平面PMN⊥平面PAD.
平面PMN,∴平面PMN⊥平面PAD.
(II)![]() 平面PBA的一个法向量为
平面PBA的一个法向量为![]() .
.
∵直线PC与平面PBA成角的正弦值为![]()
即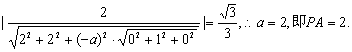
(III)由(I),MN⊥平面PAD,知PM⊥MN,MQ⊥MN,
∴∠PMQ即为二面角P—MN—Q的平面角.
而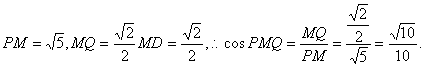
18、解:(1)延长![]() 到
到![]() 使
使![]() ,连结
,连结![]() 、
、![]() ,
,![]() 是
是![]() 中点,所以
中点,所以![]() .
.
故直线![]() 和
和![]() 所成的锐角(或直角)就是
所成的锐角(或直角)就是![]() 和
和![]() 所成的角…2分
所成的角…2分
∵![]() 平面
平面![]() ∴
∴![]() ,又
,又![]() . ∴
. ∴![]() .
.
![]() 是
是![]() 中点,故
中点,故![]() .所以
.所以![]() ,又
,又![]() ,因此
,因此![]() 为等边三角形.所以
为等边三角形.所以![]() ∴直线
∴直线![]() 和
和![]() 所成的角是
所成的角是![]()
(2)设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]()
∵![]() ,
,![]() ,
,![]() ∴
∴![]()
(3)由上可知,![]() ,又
,又![]() 是
是![]() 中点,故
中点,故![]() ,
,
由平面![]() 平面
平面![]() ,∴应
,∴应![]() 平面
平面![]()
故![]() ,即
,即![]() 应为过
应为过![]() 的
的![]() 的垂线和
的垂线和![]() 的交点.
的交点.
由![]() ,所以
,所以![]() 的中垂线过
的中垂线过![]() 点,即
点,即![]() 为
为![]() 点.
点.
19、解:(I)证明:在△ABC中,AC=BC,M为AB的中点,∴CM⊥AB,
又∵三棱柱ABC-A1B1C1是直三棱柱,
∴平面ABB1A1⊥平面ABC ∴CM⊥平面ABB1A1,
而CM![]() 平面CMD, ∴平面CMD⊥平面ABB1A1
平面CMD, ∴平面CMD⊥平面ABB1A1
 (II)解法一
(II)解法一
过M作ME⊥BD于E,连结CE,
∵CM⊥平面ABB1A1
∴ME是CE在平面ABB1A1上的射影,∴CE⊥BD, 所以∠CEM是二面角![]() 的平面角.
的平面角.
由![]() =1,则AB=
=1,则AB=![]() ,
,![]() ,
,
取MB的中点F,则BF=![]() ,
,
∴![]()
由![]() 得:
得:![]()
 在Rt△CME中,tan∠CEM=
在Rt△CME中,tan∠CEM=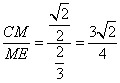
所以∠CEM=![]()
即二面角![]() 的大小是
的大小是![]()
解法二(向量法):以C为原点,分别以CA 、CB、CC1所在直线为x、y、z轴,建立如图所示空间直角坐标系,令![]() =1,
=1,
则C(0,0,0),A(1,0,0),A1(1,0,1),
B(0,1,0),B1(0,1,1),M(![]() ,
,![]() ,0),
,0),
D(![]() ,
,![]() ,1),C1(0,0,1),
,1),C1(0,0,1),
∴![]() ,
,![]() .
.
设平面CBD的法向量为![]() ,则
,则
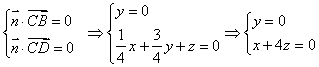 取
取![]() ,则
,则![]() ,∴
,∴![]() .
.
而平面MBD的法向量是![]() =(
=(![]() ,
,![]() ,0),
,0),
∴cos<![]() ,
,![]() >=
>=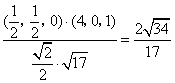 ,即<
,即<![]() ,
,![]() >=
>=![]()
如图可知,二面角![]() 为锐角,∴二面角
为锐角,∴二面角![]() 的大小为
的大小为![]()