第Ⅰ卷 (选择题 共60分)
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.函数y=2sin(2x＋)＋1的最小正周期是( )
A. B. C. π D. 2π
2.在复平面内, 复数 对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.函数y=f(x)与函数y=log2x 的图象关于直线x=0 对称, 则( )
A. f(x)=－2x B. f(x)=2x C. f(x)=log2(－x) D. f(x)=－log2x
4.设α、β是两个不同平面, m,n是两条不同的直线, 则下列命题正确的是( )
A. 若m∥n , 且 m⊥α, n⊥β, 则α∥β B. 若mÌα, nÌβ, 且α∥β, 则m∥n
B.若m、nÌα, 且m∥β, n∥β, 则α∥β D.若α⊥β, mÌα, nÌβ, 则m⊥n
5.已知向量=(, ), 向量= (, － ) , 曲线·=1上一点P到F(3,0)的距离为6, Q为PF的中点, O为坐标原点, 则OQ =( )
A. 1 B.2 C.5 D. 1或5
6.已知无穷数列{an}是各项均为正数的等差数列, 则有( )
A. < B. ≤ C. > D. ≥
7. 若(x－)6的展开式中的第五项等于 , 则n→∞lim( ＋ ＋ ＋ … ＋ )= ( )
A. 1 B. C. D.
8.设f(x)=cosx－sinx把f(x)的图象按向量=(m,0) (m>0)平移后, 图象恰好为函数y=－f '(x)的图象, 则m 的值可以为( )
A. B. C. D. π
9.抛物线y2=ax(a≠0)的准线与x轴交于点P , 直线l 经过点P, 且与抛物线有公共点,则直线l 的倾斜角的取值范围是( )
A. [0, ] B. [0, ]∪[,π) C. [,] D. [,]∪(,]
10.正三棱锥底面边长为a, 侧棱与底面成角为60°, 过底面一边作一截面使其与底面成30°的二面角, 则此截面的面积为( )
A. a2 B. a2 C. a2 D. a2
11.定义在R上的函数y=f(x)满足: f(－x)=－f(x), f(1＋x)=f(1－x), 当x∈[－1,1]时, f(x)=x3,则f(2007)的值是( )
A. －1 B.0 C. 1 D. 2
12. 对于任意的x∈R, 不等式 2x2－a＋3>0恒成立, 则实数a 的取值范围是( )
A. a<2 B. a≤2 C. a<3 D. a≤3
第Ⅱ卷 (非选择题 共90分)
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在横线上。
13.函数y=ex＋1的反函数是_________
14. 已知平面区域D是由以A(1,3),B(2,0), C(3,1)为顶点的三角形内部和边界组成, 若目标函数z=ax＋y(a>0) 在区域D内仅在点(2,0)处取 得最小值, 则a的取值范围为_______
15. 一名同学想要报考某大学, 他必须从该校的7个不同专业中选出5个, 并按第一志愿, 第二志愿, …, 第五志愿的顺序填进志愿表, 若A 专业不能作为第一, 第二志愿, 则他共有______种不同的填法( 用数字作答)
16. 下列四个命题: ①圆(x＋2)2＋(x＋1)2=4 与直线x－2y=0相交, 所得弦长为2;
②直线y=kx 与圆 (x－cosθ)2＋(y－sinθ)2=1恒有公共点;
③ 若棱长为3的正方体的顶点都在同一球面上, 则该球的的表面积为108π.
④若棱长为的正四面体的顶点都在同一球面上, 则该球的体积为π.
其中, 下确命题的序号为_________(写出所有正确命题的序号)
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17.(本小题满分12分)
已知△ABC的三个内角A, B,C 所对的边分别是a,b,c, 向量 = (1,1－sinA) ,
=(cosA, 1) 且⊥.
(1) 求角A; (2) 若b＋c= a , 求sin(B＋)的值.
18. (本小题满分12分)
在一次语文测试中, 有道把我国四大文学名著《水浒传》、《三国演度》、《西游记》、《红楼梦》与它们的作者连线的题目, 每连对一个得3分, 连错不得分, 一位同学该题得ξ分.
(1)求该同学得分不少于6分的概率;
(2)求ξ的分布列及数学期望.
19. (本小题满分12分)
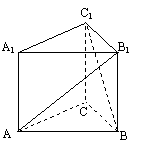如图正三棱柱ABC－A1B1C1中,底面边长为a, 侧棱长为a, 若经过AB1且与BC1平行的平面交上底面于D点.
(1)试确定点D的位置, 并证明你的结论;
(2)求二面角A1－AB1－D的大小
20.( 本小题满分12分)
已知函数f(x)= , 数列{an}满足a1=1, an＋1=f(an) (n∈N*)
(1) 求数列{an}的通项公式;
(2)若数列{bn}满足bn= anan＋1·3n, Sn=b1＋b2＋…＋bn, 求Sn .
21. ( 本小题满分12分)
椭圆C 中心为坐标原点O , 焦点在y轴上, 焦点到相应的准线的距离以及离心率均为, 直线l 与y轴交于点P(0,m) 与椭圆O交于相异两点A、B, 且=λ.
(1)求椭圆方程;
(2)若＋λ =4, 求m 的取值范围.
22. ( 本小题满分12分)
已知函数f(x)=ax－x (a>1)
(1) 求函数f(x)的最小值, 并求最小值小于0时a的取值范围.
(2)令S(n)=Cn1f '(1)＋Cn2f '(2)＋ … ＋Cnn－1f '(n－1),
证明: S(n)>(2n－2)·f '()
参考答案
1.C 2.B 3.C 4.A 5.D 6.B 7.A 8.B 9.B 10.D 11.A 12.C
13. y=lnx－1(x>0) 14. (0,3) 15. 1800 16. ②④
17.解: (1) ∵⊥, ∴·=0, ∴cosA＋1－sinA=0 sinA－cosA=1,
sin(A－)= . ∵0<A<π, ∴－< A－<, ∴A－ = , ∴A=
(2) ∵b＋c= a, ∴由正弦定理得: sinB＋sinC= sinA =
∵B＋C= , ∴sinB＋sin(－B)= , cosB＋sinB=
即 sin(B＋) =
18.解: (1)ξ的可能取值为0, 3, 6, 12 P(ξ=12)= = , P(ξ= 6) = = =
该同学得分不少于6分的概率为P=P(ξ= 6) ＋ P(ξ=12) =
(2)P(ξ=3)= = , P(ξ=0)=1－ － － =
| ξ | 0 | 3 | 6 | 12 |
| P |
ξ的分布列为:
数学期望:Eξ=0× ＋ 3× ＋ 6× ＋ 12× =3
19. 解: (1) D为A1C1的中点, (D也可以是△A1B1C1的边A1C1中线上任一点).连结A1B与AB1交于E. 则E为A1B的中点, DE为平面ABB1A1D与平面A1BC1的交线,
∵BC1∥平面AB1D, ∴BC1∥DE, ∴D为为A1C1的中点
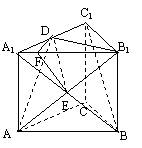(2)过D作DF⊥A1B于F, 由正三棱柱的性质, AA1⊥DF, ∴DF⊥平面ABB1,
连结EF, DE, 在正三角形A1B1C1中, ∵D是A1C1的中点, ∴B1D= A1B1= a, 又在直角三角形AA1D中, ∵AD= = a , ∴AD=B1D,
∴DE⊥AB1, ∴可得EF⊥AB1, 则∠DEF为二面角A1－AB1－D的平面角. 可求得DF= a ∵△B1FE∽ △B1AA1, 得EF=a
∴ ∠DEF= , 即为所求.
20. 解: (1) 由已知: an＋1= , ∴ = ＋1, ∴ + = 3( ＋ ), 并且
＋ = ∴数列{ ＋ }为以为首项, 3为公比的等比数列
∴ ＋ = ·3n－1, ∴ an=
(2)bn= = －
∴Sn= b1＋b2＋…＋bn = － ＋ － ＋ …＋ －
= －
21.解: (1) 设＋ = 1 (a>b>0), 设c>0, c2=a2－b2, 由条件知: －c = = ,
∴a=1, b=c= 故C的方程为: y2＋ =1
(2) 由=λ 得－ =λ(－) ∴(1＋λ) = ＋ λ
∴ 1＋λ =4 , λ=3, 设l与椭圆C交点为A(x1,y1),B(x2,y2)
得 (k＋2)x2＋2kmx＋(m2－1)=0
△= (2km)2－4(k2＋2)(m2－1)=4(k2－2m2＋2)>0 (*)
x1＋x2= , x1x2= ∵=3 ∴－x1=3x2, ∴ x1＋x2=－2x2, x1x2=－3x22,再消去x2, 得3(x1＋x2)2＋4x1x2=0 , ∴3()2＋4=0 整理得4k2m2＋2m2－k2－2=0
m2= 时, 上式不成立, m2≠ 时, k2= 由(*)式得k2>2m2－2 因λ=3, ∴k≠0,
∴k2= >0, ∴－1<m<－, 或<m<1
即所求m的取值范围为(－1,－)∪( , 1)
22.(1) 由f '(x)=axlna－1 f '(x)>0 即: axlna>1, ∴ax> , 又a>1, ∴x>－logalna
同理: f '(x) <0, 有x<－logalna 所以f '(x)在(－∞, －logalna)上递减, 在(－logalna, ＋∞)
上递增, 所以f(x)max=f(－logalna) = , 若f(x)max<0, 即 <0, 则
ln(lna)<－1, ∴lna< ∴ a 的取值范围是 1<a< 
(2) S(n)=Cn1(alna－1)＋Cn2(a2lna－1)＋ … ＋Cnn－1(an－1lna－1),
= (Cn1a＋Cn2a2＋…＋Cnn－1an－1)lna－(Cn1＋Cn2＋…＋Cnn－1)
= [Cn1(a＋an－1)＋Cn2(a2＋an－2)＋＋Cnn－1(an－1＋a)]lna－(2n－2)
≥ 
= 
∴ 不等式成立.