高考数学第二轮数学专题训练一
(理)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分,考试时间为120分钟.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(AB)=P(A)P(B)
如果事件A在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率是
次的概率是![]()
球的表面积公式![]() 、球的体积公式
、球的体积公式![]() ,其中
,其中![]() 表示球的半径
表示球的半径
第I卷(选择题,共50分)
一.选择题(本大题共10小题,每小题5分,50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设全集U=R,已知集合![]() ,集合
,集合![]() Z
Z![]() Z
Z![]() ,则
,则![]() (B)
(B)
A.![]() B.
B.![]() C.{0,1,3} D.
C.{0,1,3} D.![]()
提示:由![]()
![]() ,
,![]() ,求得正确选项为B.
,求得正确选项为B.
2.已知三个力![]() ,
,![]() ,
,![]() 同时作用于某物体上一点,现加上一个力
同时作用于某物体上一点,现加上一个力![]() 后恰使得物体保持平衡,则
后恰使得物体保持平衡,则![]() (B)
(B)
A.7 B.1 C.-1 D.![]()
提示:要求四个力的和为零向量,∴![]() (1,2),故
(1,2),故![]() ,选B.
,选B.
3.设复数![]() 的共轭复数用
的共轭复数用![]() 表示,已知复数
表示,已知复数![]() 在映射f下的象为
在映射f下的象为![]() ,且
,且![]() 在
在![]() 下存在原象,则它的原象为( A )
下存在原象,则它的原象为( A )
A.2 B.![]() C.
C.![]() D.
D.![]()
提示:令![]()
![]() ,则
,则![]() ,∴
,∴![]() ,故原象为
,故原象为![]() ,故选A.
,故选A.
4.如果一个点既在一个指数函数的图象上又在一个对数函数的图象上,那么就称这个点为“优质点”.在下面五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,![]() )中,“优质点”的个数为(B)
)中,“优质点”的个数为(B)
A.1个 B.2个 C.3个 D.4个
提示:若为对数函数图象上的点,则当![]() 时,
时,![]() ,∴M、N两点不符合条件,若为指数函数图象上的点,则当
,∴M、N两点不符合条件,若为指数函数图象上的点,则当![]() 时才有
时才有![]() ,∴P点不符合条件,反之在找到指数函数
,∴P点不符合条件,反之在找到指数函数![]() ,使
,使![]() 和
和![]() 成立的同时可以找到对数函数
成立的同时可以找到对数函数![]() ,使
,使![]() 和
和![]() 成立,故选B.
成立,故选B.
5.用一个平面去切一个正四面体,使之得到形状大小都相同的两个几何体,则这样的平面共有(D)
A.3个 B.6个 C.12个 D.无数个
提示:过其中一组对棱的两个中点,且与另一组对棱相交的平面都满足条件,选D.
6.已知![]() ,则圆锥曲线
,则圆锥曲线![]() 的一条准线方程是(C)
的一条准线方程是(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
提示:由已知得![]() ,∴
,∴![]() ,∴圆锥曲线的标准方程为
,∴圆锥曲线的标准方程为![]() ,其渐近线方程为
,其渐近线方程为![]() ,故选C.
,故选C.
7.如果数列![]() 满足
满足![]() ,则
,则![]() ( A
)
( A
)
A.2 B.1 C.![]() D.0
D.0
提示:依题意有![]() ,∴
,∴![]() ,即数列
,即数列![]() 是等差数列,公差为
是等差数列,公差为![]() ,首项为
,首项为![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故选A.
,故选A.
8.已知函数![]() 的反函数是
的反函数是![]() ,且
,且![]() ,则
,则![]() 的最小值是(D)
的最小值是(D)
A.2 B.4 C.![]() D.
D.![]()
提示:由已知![]() ,∴
,∴![]() ,即
,即![]() ,即
,即![]() ,且
,且![]() 都为正数,∴
都为正数,∴![]() ,故选D.
,故选D.
9.曲线![]() 上的点到直线
上的点到直线![]() 的最短距离是(A)
的最短距离是(A)
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
提示:令![]() ,则
,则![]() ,∴曲线上过点(1,0)的切线与直线
,∴曲线上过点(1,0)的切线与直线![]() 平行,从而最短距离即为点(1,0)到直线
平行,从而最短距离即为点(1,0)到直线![]() 的距离,由距离公式得
的距离,由距离公式得![]() ,选A.
,选A.
 10.若函数
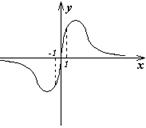
10.若函数![]() 的图象如图所示,则m的取值范围为(B)
的图象如图所示,则m的取值范围为(B)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
提示:![]() ,由图象可知
,由图象可知![]() 必有两个绝对值大于1的实数根,∴
必有两个绝对值大于1的实数根,∴![]() ,又在
,又在![]() 上函数单调递增,∴
上函数单调递增,∴![]() ,故选B.
,故选B.
二.填空题(本大题共5小题,每小题5分,共25分,把答案填在题中横线上)
11.已知函数![]() 的最小正周期为
的最小正周期为![]() ,则
,则![]() ____________.
____________.
[答案]1
提示:![]() ,∴最小正周期
,∴最小正周期![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
12.设O为坐标原点,A(2,1),若P![]() 的坐标满足
的坐标满足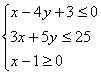 ,则
,则![]() 的最大值为
.
的最大值为
.
[答案]![]()
提示:作出可行域,设取得最大值的点为![]() ,则
,则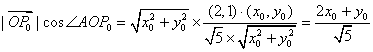 ,令
,令![]() ,由图形可知当该直线系经过
,由图形可知当该直线系经过![]() 与
与![]() 的交点
的交点![]() 时
时![]() 有最大值12,故为
有最大值12,故为![]() .
.
13.设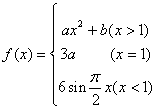 ,若
,若![]() 在
在![]() 处连续,则
处连续,则![]() __________.
__________.
[答案]![]()
提示:当点处的极限值等于其函数值,∴![]() ,∴
,∴![]() ,
,![]() ,故得
,故得![]() .
.
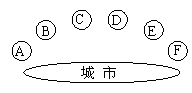 14.某市为改善投资环境,计划对城郊结合部如图所示的A、B、C、D、E、F六个区域进行治理,第一期工程拟从这六个区域中选取三个区域,但要求至多有两个区域相邻,则不同的选取方法共有____________种(用数字作答).其中区域A在第一期得到治理的概率是_______________.
14.某市为改善投资环境,计划对城郊结合部如图所示的A、B、C、D、E、F六个区域进行治理,第一期工程拟从这六个区域中选取三个区域,但要求至多有两个区域相邻,则不同的选取方法共有____________种(用数字作答).其中区域A在第一期得到治理的概率是_______________.
[答案]16,![]()
提示:分两类,第一类,恰有两个区域相邻——当AB或EF相邻时各有3种,当BC、CD、DE相邻时各有2种;三个区域都不相邻——有![]() 种方法;故共有16种方法.
种方法;故共有16种方法.
其中含有A的方法有ABD(E、F),ACD(DE、EF、DF)和ACE(F)9种,故所求概率为![]() .
.
15.对大于2或等于2的自然数![]() 的
的![]() 次幂进行如下方式的“分裂”:
次幂进行如下方式的“分裂”:
![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
则对![]() 进行类似的“分裂”时,“分裂”中的最大的数是____________;若已知
进行类似的“分裂”时,“分裂”中的最大的数是____________;若已知![]() 在“分裂”中的最小数是21,则
在“分裂”中的最小数是21,则![]() 的值为______________.
的值为______________.
[答案]9,5
提示:由![]() 得
得![]() “分裂”中的最大的数是9;又
“分裂”中的最大的数是9;又![]() ,而
,而![]() ,故知若
,故知若![]() 在“分裂”中的最小数是21,则
在“分裂”中的最小数是21,则![]() 的值为5.
的值为5.
三.解答题:(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤)
16.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 且
且![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,求
,求![]() 的值.
的值.
[解答]![]() ,
,
(1)当![]() 时,
时,![]() ,
,
∴当![]() (
(![]() )时
)时![]() 是增函数,
是增函数,
∴![]() 的单调递增区间是
的单调递增区间是![]() (
(![]() );
);
(2)由![]() 得
得![]() ,
,
∴![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 取得最小值为3,
取得最小值为3,
而当![]() 时,
时,![]() 取得最大值为4,
取得最大值为4,
即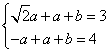 ,解得
,解得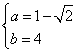 ,∴
,∴![]() .
.
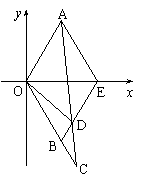 17.(本小题满分12分)如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使BC=t(t>0),连AC交BE于D点.
17.(本小题满分12分)如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使BC=t(t>0),连AC交BE于D点.
(1)用t表示向量![]() 和
和![]() 的坐标;
的坐标;
(2)求向量![]() 和
和![]() 的夹角的大小;
的夹角的大小;
(3)求![]()
![]() 的取值范围。
的取值范围。
[解答](1)![]() =((t+1),-(t+1)),
=((t+1),-(t+1)),
∵![]() =t
=t![]() ,∴
,∴![]() =t
=t![]() ,
,![]() =
=![]() ,又
,又![]() =(,),
=(,),
![]() =
=![]() -
-![]() =(t,-(t+2));∴
=(t,-(t+2));∴![]() =(,-),
=(,-),
∴![]() =(,-);
=(,-);
(2)∵![]() =(,-),
=(,-),
∴![]() ·
·![]() =·+·=,
=·+·=,
又∵![]() ·
·![]() =
=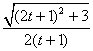 ·
·![]() ,
,
∴cos<![]() ,
,![]() >==,∴向量
>==,∴向量![]() 与
与![]() 的夹角为60°;
的夹角为60°;
(3)由(2)![]() ·
·![]() =
=![]() ,
,
∴![]() ·
·![]() ,且等号不能取得,
,且等号不能取得,
∴![]() ·
·![]() ,所求范围是
,所求范围是![]() 。
。
18.(本小题满分12分)一种电器控制器在出厂时每五件一等品装成一箱,工人在装箱时不小心把两件二等品和3件一等品装入了一箱,为了找出该箱中的二等品,我们把该箱中产品逐一取出进行测试.
(1)求前两次取出都是二等品的概率;
(2)求第二次取出的是二等品的概率;
(3)用随机变量![]() 表示第二个二等品被取出时共取出的产品件数,求
表示第二个二等品被取出时共取出的产品件数,求![]() 的分布列及数学期望.
的分布列及数学期望.
[解答](1)五件产品逐一取出方法共有![]() 种,
种,
前两次取出都是二等品的方法共有![]() 种,
种,
所以前两次取出都是二等品的概率为![]()
(2)第二次取出是二等品方法共有![]() 种,
种,
所以第二次取出是二等品的概率是:![]() ;
;
(3)依题意![]() ,
,
![]() ,
,![]()
|
| 2 | 3 | 4 | 5 |
| P |
|
|
|
|
所以分布列为:
∴![]() .
.
 19.(本小题满分12分)如图,已知三棱柱ABC—A1B1C1的棱长都是2,点A1与AB、AC的距离都等于
19.(本小题满分12分)如图,已知三棱柱ABC—A1B1C1的棱长都是2,点A1与AB、AC的距离都等于![]() ,且A1E⊥B1B于E,A1F⊥C1C于F.
,且A1E⊥B1B于E,A1F⊥C1C于F.
(1)求证:平面A1EF⊥平面B1BCC1;
(2)求点A到平面B1BCC1的距离;
(3)求平面A1EF与平面A1B1C1所成二面角的大小.
[解答](1)![]() ,∴B1B
,∴B1B![]() 平面A1EF,∴平面A1EF⊥平面B1BCC1;
平面A1EF,∴平面A1EF⊥平面B1BCC1;
(2)由于A1A//平面B1BCC1,
故点A、A1与平面B1BCC1的距离相等.
∵四边形ABB1A1为菱形,故A1E=A1F=![]() ,
,
∵B1B⊥平面A1EF,EF![]() 平面A1EF,
平面A1EF,
∴BB1⊥EF,从而EF=BC=2,
∴△A1EF是等腰直角三角形,
取EF中点M,则A1M⊥EF,且A1M=1,
从而A1M⊥平面B1BCC1,即A1到平面B1BCC1的距离为1;
(3)设平面A1EF与平面A1B1C1所成的二面角的棱为直线l,取B1C1的中点N,
则A1N⊥B1C1,但B1C1//EF,∴B1C1//平面A1EF,于是B1C1//l,
在△A1B1C1中,A1N=![]() ,∴A1M⊥l,A1N⊥l,
,∴A1M⊥l,A1N⊥l,
即∠MA1N为所求二面角的平面角,
∵A1M⊥平面B1BCC1,∴A1M⊥MN,∴cos∠NA1M=![]() ,
,
故所求二面角的大小为![]() .
.
20.(本小题满分13分)在平面直角坐标系中,已知A1![]() ,A2
,A2![]() ,P(
,P(![]() ),M
),M![]() ,O为坐标原点,若实数
,O为坐标原点,若实数![]() 使向量
使向量![]() ,
,![]() 和
和![]() 满足
满足![]() .
.
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当![]() 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线![]() 上找到一点C,恰使
上找到一点C,恰使![]() 为正三角形?请说明理由.
为正三角形?请说明理由.
[解答](1)由已知可得![]() ,
,![]() ,
,![]() ,且
,且![]() ,∴
,∴![]() 即
即![]() ,
,
即点P的轨迹方程是![]() ,
,
当![]() 即
即![]() 时,有
时,有![]() ,
,
此时![]() ,∴
,∴![]() ,综合
,综合![]() 知此时点的轨迹即为两点A1和A2;
知此时点的轨迹即为两点A1和A2;
当![]() 即
即![]() 时,方程为
时,方程为![]() ,
,
此时点P的轨迹是双曲线;
当![]() 时,方程为
时,方程为![]() ,且
,且![]() 为两条射线;
为两条射线;
(2)过点A1斜率为1的直线方程为![]() ,
,
当![]() 时,曲线方程为
时,曲线方程为![]() ,其轨迹就是两点A1和A2,
,其轨迹就是两点A1和A2,
此时直线![]() 过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在.
过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在.
21.已知函数![]() ,记
,记![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的前
的前![]() 项和;
项和;
(2)解关于![]() 的不等式
的不等式![]() ;
;
(3)证明![]() .
.
[解答](1)∵![]() ,
,
![]() ,
,
……
![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,∴
,∴![]()
![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
(2)当![]() 时,
时,![]() 成立,故
成立,故![]() 是不等式
是不等式![]() 的一个解,
的一个解,
当![]() 时,
时,![]() 成立,故
成立,故![]() 不是不等式
不是不等式![]() 的解,
的解,
当![]() 时,
时,![]() 成立,故
成立,故![]() 也不是不等式
也不是不等式![]() 的解,
的解,
当![]() ,
,![]() 时,∵
时,∵![]() ,
,
∴故![]() ,故
,故![]() ,
,![]() 都是不等式
都是不等式![]() 的解,
的解,
综合知所求的解集为![]()
![]() ,且
,且![]() ;
;
(3)∵![]() ,
,
且由(2)知![]() ,
,
∴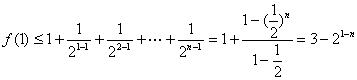 .
.