高考数学第十次综合考试
数学试卷
说明:1.本试卷分第І卷(选择题)和第П卷(非选择题)两部分。满分150分。考试时间120分钟。
2.请将选择题的答案填涂在答题卡上。
第І卷(选择题共50分)
一、选择题:本大题共10小题,每小题5分,共50分。
1.设集合![]() ,
,![]() 则满足
则满足![]() 的集合C的个数是
的集合C的个数是
(A)0 (B)1 (C)2 (D)3
2.已知![]() 、
、![]() 为两个非零向量,有以下命题:①
为两个非零向量,有以下命题:①![]() 2=
2=![]() 2 ②
2 ②![]() ·
·![]() =
=![]() 2 ③
2 ③![]() =
=![]() 且
且![]() //
//![]() ,其中可以作
,其中可以作![]() =
=![]() 的必要但不充分条件的命题的
的必要但不充分条件的命题的
(A)② (B)①③ (C)②③ (D)①②③
3.过抛物线![]() 的焦点的弦AB两端点的横坐标分别是
的焦点的弦AB两端点的横坐标分别是![]() 、
、![]() ,若
,若![]() ,则AB 的长为
,则AB 的长为
(A)10 (B)
4.把函数![]() 的图像向左平移2个单位,再向下平移1个单位,所得图像的函数解析式为
的图像向左平移2个单位,再向下平移1个单位,所得图像的函数解析式为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.在等比数列![]() 中,
中,![]() ,则
,则![]() 的值为
的值为
(A)-432 (B)432 (C)-216 (D)以上都不对
6.已知:![]() 是直线,
是直线,![]() 是平面,给出下列四个命题:(1)若
是平面,给出下列四个命题:(1)若![]() 垂直于
垂直于![]() 内的两条直线,则
内的两条直线,则![]() ;(2)若
;(2)若![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;(3)若
内的所有直线;(3)若![]() 且
且![]() 则
则![]() ;(4)若
;(4)若![]() 且
且![]() 则
则![]() ;(5)若
;(5)若![]() 且
且![]() 则
则![]()
![]() 。
。
其中正确命题的个数是
(A) 0 (B) 1 (C) 2 (D) 3
7.函数![]() 其定义域
其定义域![]() 分成了四个单调区间,则实数
分成了四个单调区间,则实数![]() 满足
满足
(![]() )
) ![]() (
(![]() )
) ![]()
(![]() )
) ![]() (
(![]() )
)![]()
8.数列![]() 中,
中,![]() ,则该数列前100项中的最大项与最小项分别为
,则该数列前100项中的最大项与最小项分别为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.椭圆![]() (
(![]() )的两焦点分别为
)的两焦点分别为![]() 、
、![]() ,以
,以![]()
![]() 为边作正三角形,
为边作正三角形,
若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.若![]() 是双曲线
是双曲线![]() (
(![]() )上一点,且满足
)上一点,且满足![]() ,则该点P一定位于双曲线的
,则该点P一定位于双曲线的
(A)右支上 (B)上支上 (C)右支或者上支上 (D)不能确定
第П卷(非选择题共100分)
二、填空题:本大题共6小题,每小题5分,共30分。
11.曲线在![]() 在
在![]() 处的切线的倾斜角为
。
处的切线的倾斜角为
。
12.与双曲线![]() 有共同的渐近线,且经过点A
有共同的渐近线,且经过点A![]() 的双曲线的一个焦点到一条渐近线的距离是
。
的双曲线的一个焦点到一条渐近线的距离是
。
13.若正数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的最大值为 。
的最大值为 。
14.若点![]() ,点
,点![]() ,且
,且![]() ,则过点P且在两坐标轴上有相等截距的直线方程是
。
,则过点P且在两坐标轴上有相等截距的直线方程是
。
15.如果直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称,则不等式组
对称,则不等式组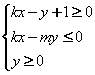 所表示的平面区域的面积是
.
所表示的平面区域的面积是
.
16.给出下列五个命题:①不等式![]() 的解集为
的解集为![]() ;
;
②若函数![]() 为偶函数,则
为偶函数,则![]() 的图象关于
的图象关于![]() 对称;
对称;
③若不等式![]() 的解集为空集,必有
的解集为空集,必有![]() ;
;
④函数![]() 的图像与直线
的图像与直线![]() 至多有一个交点;
至多有一个交点;
⑤若角![]() ,β满足cos
,β满足cos![]() ·cos
·cos![]() =1,则
=1,则![]() +
+![]() )=0.
)=0.
其中所有正确命题的序号是 .
三、解答题:本大题共5小题,共70分。
19.(本小题满分12分)
设向量![]()
![]() ,其中
,其中![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)若函数![]() 的大小.
的大小.
20.(本小题满分14分)已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,其中
,其中![]() 在第一象限,且
在第一象限,且![]() .(Ⅰ)求点
.(Ⅰ)求点![]() 的坐标;
的坐标;
 (Ⅱ)若直线
(Ⅱ)若直线![]() 与双曲线
与双曲线![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,且线段
,且线段![]() 的中点坐标为
的中点坐标为![]() ,求实数
,求实数![]() 的值。
的值。
21.(本小题满分14分)
如图,在底面是菱形的四棱锥P—ABCD中, ![]() ,点E在PD上,且
,点E在PD上,且![]() :
:![]() :
:![]() ,
,
(Ⅰ) 证明 PA⊥平面ABCD;
(II) 在棱PD上是否存在一点F,
使BF∥平面AEC?证明你的结论.
22.(本小题满分14分)
 椭圆的中心是原点O,它的短轴长为
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )的准线
)的准线![]() 与
与![]() 轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点。
轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明![]() 。
。
23.(本小题满分16分)
在直角坐标平面上有一点列![]() ,对每个正整数
,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图象上,且
的图象上,且![]() 的横坐标构成以
的横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)设抛物线列![]() 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于![]() 轴,第
轴,第![]() 条抛物线
条抛物线![]() 的顶点为
的顶点为![]() 且过点
且过点![]() ,记过点
,记过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线的斜率为
只有一个交点的直线的斜率为![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最大数,
中的最大数,![]() ,求
,求![]() 的通项公式。
的通项公式。
江苏省姜堰高级中学2007届第十次综合考试数学试卷答案07。03。18
一、选择题
CDBBA BBCCA
二、填空题
11.![]() 12.2 13.
12.2 13.![]() 14.
14.![]() 或
或![]()
15.![]() 16.②④⑤
16.②④⑤
三、解答题
17.解:(I)∵![]() (2分)
(2分)
∴![]() ,
(4分)
,
(4分)
∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() 。
(6分)
。
(6分)
(II)∵![]() ,
,
![]() , (8分)
, (8分)
∴![]() ,
(10分)
,
(10分)
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 。 (12分)
。 (12分)
18.解:(Ⅰ) 直线![]() 方程为
方程为![]() ,设点
,设点![]() ,
(2分)
,
(2分)
由![]() (4分)
(4分)
及![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() (6分)
(6分)
(Ⅱ)由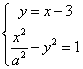 得
得![]() ,
(9分)
,
(9分)
设![]() ,则
,则![]() ,得
,得![]() , (12分)
, (12分)
此时,![]() ,∴
,∴![]() 。
(14分)
。
(14分)
(注:缺少![]() 扣1分,
扣1分,![]() 这个不等式可解可不解。)
这个不等式可解可不解。)
19.证明:(Ⅰ)证明 因为底面ABCD是菱形, ∠ABC=60º,
所以AB=AD=AC=![]() 。
(2分)
。
(2分)
在△PAB中,由![]() , 知PA⊥AB。
(5分)
, 知PA⊥AB。
(5分)
同理, PA⊥AD,所以PA⊥平面ABCD。 (7分)
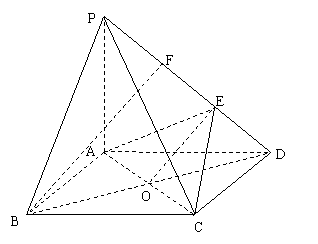 (II)当点F是棱PE的中点时,有BF∥平面AEC。(8分)
(II)当点F是棱PE的中点时,有BF∥平面AEC。(8分)
取PE的中点F,连结AF,∵![]() :
:![]() :
:![]() ,
,
∴E为DF的中点。 (10分)
连结BD,交AC于O,连结OE,则有OE∥BF。(12分)
又OE![]() 平面AEC,BF
平面AEC,BF![]() ∥平面AEC,
∥平面AEC,
故BF∥平面AEC。 (14分)
(若从平行探索到F为中点而没有给出证明,扣2分。)
20.(1)解:由题意,可设椭圆的方程为![]() 。
。
由已知得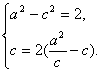
解得![]() (2分)
(2分)
所以椭圆的方程为![]() ,离心率
,离心率![]() 。 (4分)
。 (4分)
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为![]() 。由方程组
。由方程组
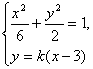
得![]() (5分)
(5分)
依题意![]() ,得
,得![]() 。 (6分)
。 (6分)
设![]() ,则
,则
![]() , ①
, ①
![]() 。 ②
。 ②
由直线PQ的方程得![]() 。于是
。于是
![]() 。 ③
。 ③
∵![]() ,∴
,∴![]() 。 ④ (7分)
。 ④ (7分)
由①②③④得![]() ,从而
,从而![]() 。 (8分)
。 (8分)
所以直线PQ的方程为![]() 或
或![]() 。 (9分)
。 (9分)
(3)证明:![]() 。由已知得方程组
。由已知得方程组
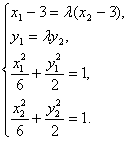 (10分)
(10分)
注意![]() ,解得
,解得![]() (12分)
(12分)
因![]() ,故
,故![]()
![]() ,而
,而![]() ,
,
所以![]() 。 (14分)
。 (14分)
21.解:(1)∵![]() 的横坐标构成以
的横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() ,
,
∴![]() , (2分)
, (2分)
∵![]() 位于函数
位于函数![]() 的图像上,
的图像上,
∴![]() , (3分)
, (3分)
∴点![]() 的坐标为
的坐标为![]() 。 (4分)
。 (4分)
(2)据题意可设抛物线![]() 的方程为:
的方程为:![]() ,
,
即![]() ,
(5分)
,
(5分)
∵抛物线![]() 过点
过点![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() , (6分)
, (6分)
∵过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线即为以
只有一个交点的直线即为以![]() 为切点的切线,
为切点的切线,
∴![]() , (7分)
, (7分)
∴![]() (
(![]() )
)
∴![]()
![]()
∴![]()
![]() 。 (10分)
。 (10分)
(3)∵![]() ,
,![]()
∴![]() 中的元素即为两个等差数列
中的元素即为两个等差数列![]() 与
与![]() 中的公共项,它们组成以
中的公共项,它们组成以![]() 为首项,以
为首项,以![]() 为公差的等差数列,
(11分)
为公差的等差数列,
(11分)
∵![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 是
是![]() 中的最大数,
中的最大数,
∴![]() ,其公差为
,其公差为![]() ,
,
10当![]() 时,
时,![]() ,
,
此时![]() ,∴不满足题意,舍去;(14分)
,∴不满足题意,舍去;(14分)
20当![]() 时,
时,![]() ,
,
此时![]() ,
,
∴![]() ;
;
30当![]() 时,
时,![]() ,
,
此时![]() ,∴不满足题意,舍去。(16分)
,∴不满足题意,舍去。(16分)
综上所述所求通项为![]() 。 (16分)
。 (16分)