高考数学直线与平面专题辅导

直线与平面专题辅导

1．在下列关于直线l、m与平面α、β的命题中,真命题是　　　　　　　　　　 (　　)

(A)若lβ且α⊥β,则l⊥α.　　　　 (B) 若l⊥β且α∥β,则l⊥α.

(C) 若l⊥β且α⊥β,则l∥α.　　　　(D) 若α∩β=m且l∥m,则l∥α.

2．把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的棱锥体积最大时，直线BD和平面ABC所成的角的大小为　　　　　　　　 　　　　　　　　　 (　　)

 （A）90^o　　　 　 （B）60^o　  　　　 （C）45^o　　　 （D）30^o

3．已知平面α与β所成的二面角为80°，P为α、β外一定点，过点P的一条直线与α、β所成的角都是30°，则这样的直线有且仅有　　　　　　　　　　　　　　  (　　)

（A）1条　　　　 （B）2条　　 　　 （C）3条　　 　（D）4条

4．设P是的二面角内一点，垂足，则AB的长为　　　　　　　　　　　　　　　　　　　 （　　）

(A) 　　　　　(B)　　　　　　(C)　　　　(D)

5．在棱长为2的正方体中，O是底面ABCD的中心，E、F分别是、AD的中点。那么异面直线OE和所成的角的余弦值等于________________.

6．已知平面a与平面b交于直线l，P是空间一点，PA⊥a，垂足为A，PB⊥b，垂足为B，且PA=1，PB=2，若点A在b内的射影与点B在a内的射影重合，则点P到l的距离为________.

7．如图，在长方体中，已知，分别是线段上的点，且

(1)求二面角的正切值;　(2)求直线与所成角的余弦值

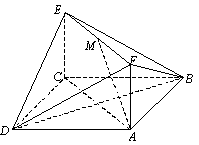8．如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=，AF=1，M是线段EF的中点。
（1）求证AM//平面BDE；

（2）求二面角A-DF-B的大小；
（3）试在线段AC上确定一点P，使得PF与BC所成的角是60°。

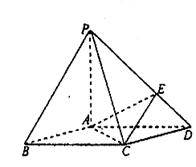
9．如图,在底面是菱形的四棱锥P—ABCD中,点E在PD上,且PE:ED= 2: 1.

(1)证明　PA⊥平面ABCD;

(2)求以AC为棱,EAC与DAC为面的二面角θ的大小:

(3)在棱PC上是否存在一点F, 使BF∥平面AEC?证明你的结论.

10．三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3，

（1） 求证：AB ⊥ BC；　 (2)设AB=BC=，求AC与平面PBC所成角的大小.

答案:1-4 BCDC　　　5.　　 6.　　  7.

8. (1)证明略　　　　(2) 60⁰ 　　(3)P是AC的中点

9. (1)证明略　　　　(2) 30⁰ 　　(3)F是PC的中点

10.(1)证明略　　　　  (2) 30⁰