直线与平面垂直
一. 教学内容：
直线与平面垂直
二. 重点、难点：
1. 直线与平面垂直的判定
（1）
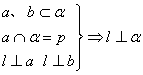判定
（2）
定义
2. 直线与平面垂直的性质
（1）
（2）
（3）*
（4）*
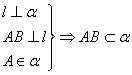
（5）*
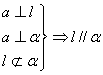
【典型例题】
[例1] 已知
，
，求证：
。
证明：
过
作平面
∴ 
∴ 
∴
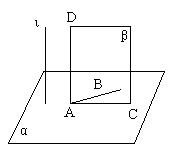
[例2] 已知，
，
，求证：
。
证明：
假设
，过A作AD∥
∵ ∴ AD⊥
确定平面
与已知矛盾 ∴ 假设不成立 ∴
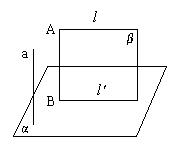
[例3] 
，
，
，求证：
。
证明：
过A作AB∥a交于B ∵ ∴ 
确定平面 
[例4] 以AB为直径的圆在平面内，
于A，C在圆上，连PB、PC过A作AE⊥PB于E，AF⊥PC于F，试判断图中还有几组线面垂直。
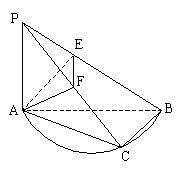
解：
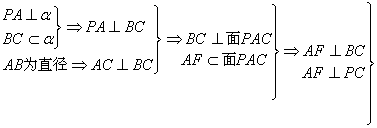
面AEF
[例5] 四面体P—ABC中，PA、PB、PC两两垂直，试判断
的形状。
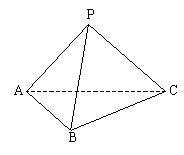
解：
，
，
为锐角，同理内角均为锐角
[例6] 求证，两条异面直线的公垂线有且只有一个。
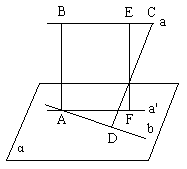
证明：存在性
过
作平面，使
，，E为上一点，过E作EF⊥于F
BE∩EF=E确定平面
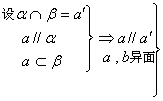
过A作AB∥EF交于B ∴ AB为公垂线
唯一性，假设存在CD为异面直线、公垂线
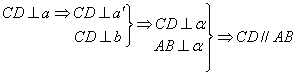
∴ A、B、C、D共面
、共面与已知矛盾
∴ 假设不成立 ∴ 公垂线有且仅有一条
[例7] 求证四个角是直角的四边形为矩形。
证明：四边形ABCD四个角均为
（1）AB、CD共面，显然成立
（2）假设AB、CD为异面直线
∴ AD、BC为AB、CD的公垂线
与两条异面直线的公垂线有且仅有一条矛盾
假设不成立 ∴ ABCD四点共面 ∴ ABCD为矩形
【模拟试题】
1. 下面结论有（ ）个正确的。
① 过定点一点作与已知直线平行的平面有且仅有一个
② 过定点一点作与已知直线垂直的平面有且仅有一个
③ 过定点一点作与已知平面平行的直线有且仅有一条
④ 过定点一点作与已知平面垂直的直线有且仅有一条
A. 1 B. 2 C. 3 D. 4
2. 已知直线、、，平面、，下列结论正确的是（ ）
A. 
B.
C. 
D.
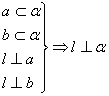
3. 是否存在四个面均为
的四面体？
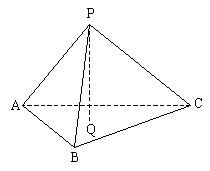
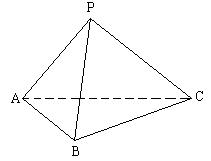
4. 四面体P—ABC中PA⊥BC，PB⊥AC，求证：PC⊥AB
【试题答案】
1. B
2. B
3. 解：存在，例4为所求。
4. 证明：
过P作PQ⊥面ABC于Q
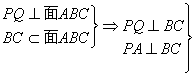
Q为垂心
面PQC
