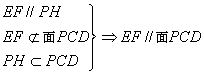直线与平面平行
一. 教学内容
直线与平面平行
二. 重点、难点
1. 直线与平面平行的判定
（1）
定义
（2）
判定
2. 直线与平面平行的性质
（1）
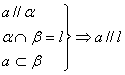
（2）* 
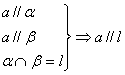
（3）* 
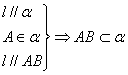
【典型例题】
[例1] 正方形ABCD交正方形ABEF于AB（如图所示）M、N在对角线AC、FB上且AM= FN。求证：MN //平面BCE
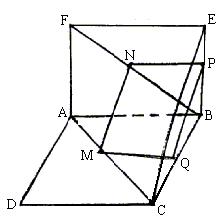
证：过N作NP//AB交BE于P，过M作MQ//AB交BC于Q
又 ∵ 
MQPN
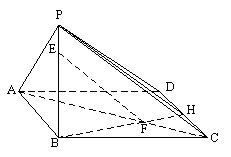
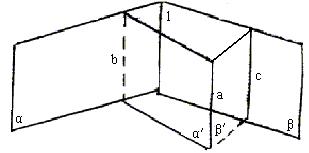
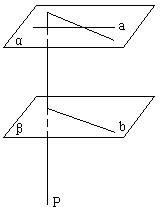
[例2] 如图，异面直线a、b，
，
，H为AB中点，
，
，
，
，
，
。求证：N为PQ中点
证：连AQ交
于M，连HM、NM
∴ 
[例3] ，
，
。求证：
证：过a作
∴ 
过a作
∴ 
∴ 
[例4] 已知
，
，
。求证：
假设
过
、A中确定平面
∵ ∴ 
又 ∵ 
与已知矛盾
∴ 假设不成立 ∴
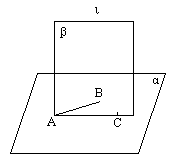
[例5] a、b异面，求证过b与a平行的平面有且仅有一个。
证：存在性：过b上一点P作直线
，
确定平面 ∴
唯一性：假设存在 
由例3 与已知矛盾 ∴ 只有一个
[例6] P为空间一点，a、b异面，过P作与a、b均平行的平面可作几个。
0个或1个 过a存在平面
过b存在平面
① 
或
0个
② 
且
1个 可用反证法证明只有一个
[例7] a、b异面直线，P为空间任一点，过P作直线与a、b均相交，这样的直线可以作多少条？
解：0、1或无数 过a存在唯一个平面
，过b存在唯一个平面
① 若或
有无数条
② 若或且
且
直线不存在
③ 且，有且只有一条
，过P、b作平面
∴
∴ 
连PQ与b相交 ∴ 存在与a、b均相交
假设有两条过P的直线
、
与a、b均相交 
确定平面
a与
各有一个交点 ∴
同理
与a、b异面矛盾
∴ 假设不成立 ∴ 只有一条
[例8] a、b、c两两异面，空间与a、b、c，均相交的直线有多少条。
证：存在
存在
c与a、b异面，c中有无数个点在、外，每一个点可作一条线与a、b均相交
∴ 无数条
【模拟试题】
1. 
，a、b与、均垂直，则a、b的关系为（ ）
A. 平行 B. 相交 C. 异面 D. 以上均可能
2. 已知异面直线a、b成60°角，P为空间一点，则过P且与a、b所成角均为60°的直线有（ ）
A. 2条 B. 3条 C. 4条 D. 无数条
3. 空间直线a，b满足（1）与a异面；（2）与a成45°角；（3）与a距离为10cm，则这样的b有（ ）
A. 1条 B. 2条 C. 4条 D. 无数条
4. P为 ABCD所在平面外一点，
，
，且
求证：
【试题答案】
1. D 2. B 3. D
4. 证：连BF交CD于H，连PH AB//CD ∴ 
∽
∴ 
在
中 
∴ 
