直线与平面平行
一. 教学内容:
直线与平面平行
二. 重点、难点:
1. 直线平面的位置关系:
(1)![]() ,直线在平面内,有无数个公共点,
,直线在平面内,有无数个公共点,
(2)![]() ,直线与平面相交,只有一个公共点。
,直线与平面相交,只有一个公共点。
(3)![]() ,直线与平面平行,无公共点。
,直线与平面平行,无公共点。
2. 直线与平面平行的判定定理:
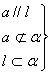
![]()
3. 直线与平面平行的性质定理:
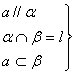
![]()
【典型例题】
[例1] ![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 。
。
证:过![]() 作
作![]()
∴ ![]()
过![]() 作
作![]()
∴ ![]()
∴
![]()
[例2] ![]() 、
、![]() 异面,求证过
异面,求证过![]() 与
与![]() 平行的平面有且仅有一个。
平行的平面有且仅有一个。
证:存在性,过![]() 上一点
上一点![]() 作直线
作直线![]()
![]() 确立平面
确立平面![]()
∴ ![]()
唯一性,假设存在![]() ,
,![]() ,
,![]()
∴
![]() ,
,![]() ,
,![]()
由例1
∴
![]() 与已知矛盾
与已知矛盾
∴ 只有一个
[例3] ![]() 为空间一点,
为空间一点,![]() 、
、![]() 异面,过
异面,过![]() 作与
作与![]() 、
、![]() 均平行的平面可作
均平行的平面可作![]() 个。
个。
![]() 个或
个或![]() 个,过
个,过![]() 存在平面
存在平面![]() ,
,![]() 。
。
过![]() 存在平面
存在平面![]() ,
,![]() 。
。
① ![]() 或
或![]()
![]() 个
个
② ![]() 且
且![]()
![]() 个
个
可用反证法证明只有一个。
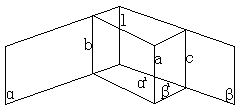
[例4] 正方形![]() 交正方形
交正方形![]() 于
于![]() ,
,![]() 、
、![]() 在对角线
在对角线![]() 、
、![]() 上,且
上,且![]() ,求证:
,求证:![]() 平面
平面![]() 。
。
证:过![]() 作
作![]() 交
交![]() 于
于![]()
过![]() 作
作![]() 交
交![]() 于
于![]()
![]() ,
,
![]()
![]()
![]() 又∵
又∵ ![]()
![]()
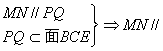 面
面![]()
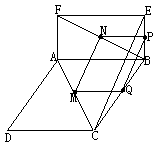
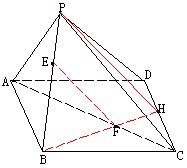
[例5] 如图,异面直线![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求:
,求:![]() 为
为![]() 中点。
中点。
证:连![]() 交
交![]() 于
于![]() ,连
,连![]() 、
、![]()
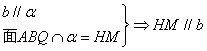
![]()
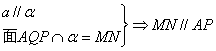
![]()
∴ ![]()
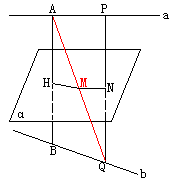
[例6] 三个平面两两相交不共线,求证三条直线交于一点或两两平行。
证:设![]() ,
,![]() ,
,![]()
∴ ![]() 、
、![]()
(1)若![]()
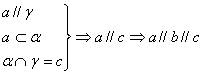
(2)若![]()
∴
![]() 、
、![]() 、
、![]() 交于一点
交于一点
![]() [例7]
[例7] ![]() 为
为 ![]() 所在平面外一点,
所在平面外一点,![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 面
面![]() 。
。
证:连![]() 交
交![]() 于
于![]() ,连
,连![]() ,
,![]()
∴
![]() ∽
∽![]()
∴
![]()
在![]() 中,
中,![]()
∴
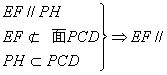 面
面![]()
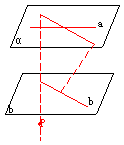
[例8] ![]() 、
、![]() 异面直线,
异面直线,![]() 为空间任一点,过
为空间任一点,过![]() 作直线
作直线![]() 与
与![]() 、
、![]() 均相交,这样的直线可以作多少条。
均相交,这样的直线可以作多少条。
解:![]() ,
,![]() 或无数。
或无数。
过![]() 存在唯一个平面
存在唯一个平面![]()
过![]() 存在唯一个平面
存在唯一个平面![]()
① 若![]() 或
或![]() ,有无数条
,有无数条
②
若![]() 或
或![]() ,且
,且![]() 且
且![]()
直线不存在
③
![]() 且
且![]() ,有且只有一条。
,有且只有一条。
![]() ,过
,过![]() 、
、![]() 作平面
作平面![]()
∴
![]()
![]()
∴
![]()
连![]() 与
与![]() 相交
相交
∴
存在![]() 与
与![]() 、
、![]() 均相交
均相交
假设有两条过![]() 的直线
的直线![]() 、
、![]() 与
与![]() 、
、![]() 均相交
均相交
![]() ,确立平面
,确立平面![]()
![]() 与
与![]() 、
、![]() 各有一个交点
各有一个交点
∴
![]()
同理![]() ,与
,与![]() 、
、![]() 异面矛盾
异面矛盾
∴ 假设不成立
∴ 只有一条
[例9] ![]() 、
、![]() 、
、![]() 两两异面,空间与
两两异面,空间与![]() 、
、![]() 、
、![]() ,均相交的直线有多少条?
,均相交的直线有多少条?
证:存在![]() ,
,![]() ,
,![]() ,
,
存在![]() ,
,![]() ,
,![]()
![]() 与
与![]() 、
、![]() 异面,
异面,![]() 中有无数个点在
中有无数个点在![]() 、
、![]() 外
外
每一个点可作一条线与![]() 、
、![]() 均相交
均相交
∴ 无数条
【模拟试题】
1. 若![]() ,
,![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.
A. 过![]() 在平面
在平面![]() 内可作无数条直线与
内可作无数条直线与![]() 平行
平行
B. 过![]() 在平面
在平面![]() 内仅可作一条直线与
内仅可作一条直线与![]() 平行
平行
C. 过![]() 在平面
在平面![]() 内可作两条直线与
内可作两条直线与![]() 平行
平行
D. 与![]() 的位置有关
的位置有关
2. ![]() ,
,![]() ,则
,则![]() 与
与![]() 的关系为( )
的关系为( )
A. 必相交 B. 必平行 C. 必在内 D. 以上均有可能
3. ![]() ,过
,过![]() 作与
作与![]() 平行的直线可作( )
平行的直线可作( )
A. 不存在 B. 一条 C. 四条 D. 无数条
4. ![]() ,
,![]() 、
、![]()
![]() ,
,![]() ,
,![]() ,则有( )
,则有( )
A. ![]() B.
B.
![]()
C. ![]() 、
、![]() 共面
D.
共面
D. ![]() 、
、![]() 异面,所成角不确定
异面,所成角不确定
5. 下列四个命题
(1)![]() ,
,![]()
![]()
(2)![]() ,
,![]()
![]()
(3)![]() ,
,![]()
![]()
(4)![]() ,
,![]()
![]()
正确有( )个
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
【试题答案】
1. B 2. A 3. D 4. B 5. A