高考数学直线和圆练习

高考数学直线和圆练习

一．考试要求：

(1)理解直线的倾斜角和斜率的概念，掌握过两点的直线的斜率公式.掌握直线方程的点斜式、两点式、一般式，并能根据条件熟练地求出直线方程.

(2)掌握两条直线平行与垂直的条件，两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系.

(3)了解二元一次不等式表示平面区域.

(4)了解线性规划的意义，并会简单的应用.

(5)了解解析几何的基本思想，了解坐标法.

(6)掌握圆的标准方程和一般方程，了解参数方程的概念，理解圆的参数方程.

【注意】本部分内容在高考中主要考查两个类型的问题：①基本概念和求直线方程；②直线与圆的位置关系等综合性试题. 求解有时还要用到平几的基本知识和向量的基本方法

三．基础公式:

1.直线的五种方程

（1）点斜式  

(直线过点，且斜率为)．

（2）斜截式 (b为直线在y轴上的截距).

（3）两点式()(、 ()).

(4)截距式(为直线横纵截距，（5）一般式(其中A、B不同时为0).

2..两条直线的平行和垂直

(1)若，

①_;②.

(2)若,,且A₁、A₂、B₁、B₂都不为零,①；②；

3.夹角公式

(1).

(，,)

(2).(,,).

直线时，直线l₁与l₂的夹角是.

4. 到的角公式 (1).

(，,)

(2).

(,,).

直线时，直线l₁到l₂的角是.

5．四种常用直线系方程

(1)定点直线系方程：经过定点的直线系方程为(除直线),其中是待定的系数; 经过定点的直线系方程为,其中是待定的系数．

(2)共点直线系方程：经过两直线

,的交点的直线系方程为

(除)，

其中λ是待定的系数．

(3)平行直线系方程：直线中当斜率k一定而b变动时，表示平行直线系方程．与直线平行的直线系方程是()，λ是参变量．

(4)垂直直线系方程：与直线 (A≠0，B≠0)垂直的直线系方程是,λ是参变量．

6.点到直线的距离

(点,直线：).

7. 或所表示的平面区域

设直线，

则或所表示的平面区域是：

若，当与同号时，表示直线的上方的区域；当与异号时，表示直线下方的区域.简言之,同号在上,异号在下.

若，当与同号时，表示直线的右方的区域；当与异号时，表示直线的左方的区域. 简言之,同号在右,异号在左.

8. 或所表示的平面区域

设曲线，则或所表示的平面区域是：

所表示的平面区域上下两部分；

所表示的平面区域上下两部分.

9. 圆的四种方程

（1）圆的标准方程 .

（2）圆的一般方程

(＞0).

（3）圆的参数方程 .

（4）圆的直径式方程 (直径端点、).

10. 圆系方程

(1)过点,的圆系方程是

,其中是直线的方程,λ是待定的系数．

(2)过直线:与

圆:的交点的圆系方程是,λ是待定的系数．

(3)过圆:与圆

:交点圆系方程是,λ是待定的系数．

11.点与圆的位置关系

点与圆的位置关系有三种若，则

点在圆外;

点在圆内.

13.直线与圆的位置关系

直线与圆的位置关系有三种:

;

;

.其中.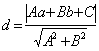

14.两圆位置关系的判定方法

设两圆圆心分别为O₁，O₂，半径分别为r₁，r₂，

;

;

;

;

.

15.圆的切线方程

(1)已知圆．

①若已知切点在圆上，则切线只有一条，其方程是当圆外时,

表示过两个切点的切点弦方程．

②过圆外一点的切线方程可设为

，再利用相切条件求k，这时必有两条切线，注意不要漏掉平行于y轴切线．

③斜率为k的切线方程可设为，再利用相切条件求b，必有两条切线．

(2)已知圆．

①过圆上的点的切线方程为

;

②斜率为的圆的切线方程为

.

16.（1）倾斜角，；

（2）；

（3）直线l与平面；

（4）l₁与l₂的夹角为，，其中l₁//l₂时夹角=0；

（5）二面角；

（6）l₁到l₂的角