高考数学模拟示范卷卷(二)
江西金太阳教育研究所数学研究室 编
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
1.若复数![]() (
(![]() 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若函数![]() 的反函数图象过点
的反函数图象过点![]() ,则函数
,则函数![]() 的图象必过点( ).
的图象必过点( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.“![]() ”是“
”是“![]() ”的( ).
”的( ).
A.必要不充分条件 B.充分不必要条件C.充要条件 D.既不充分也不必要条件
4.设集合![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的取值范围是( ).
的取值范围是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设函数![]() ,则其反函数
,则其反函数![]() 的图象( ).
的图象( ).
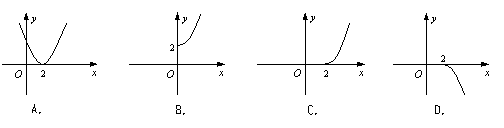 |
6.已知![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() 为直角,则“
为直角,则“![]() ”是“
”是“![]() ”的( ).
”的( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
7.球面上有三点,其中任意两点间的球面距离等于大圆周长的![]() ,经过这三点的小圆周长为
,经过这三点的小圆周长为![]() ,则球的体积为( ).
,则球的体积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若抛物线![]() 与圆
与圆![]() 相切,则公切线的方程为( ).
相切,则公切线的方程为( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
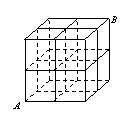
9.某建筑工地搭建的脚手架局部类似于![]() 的长方体,一建筑工人从
的长方体,一建筑工人从![]()
沿脚手架到![]() ,则行走的最近线路有( ).
,则行走的最近线路有( ).
A.![]() 种 B.
种 B.![]() 种
C.
种
C.![]() 种
D.
种
D.![]() 种
种
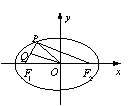 10.如图,
10.如图,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 、
、![]() 是椭圆的左、右焦点,且
是椭圆的左、右焦点,且![]() 是
是![]() 的中点,
的中点,![]() ,则点
,则点![]() 到该椭圆左准线的距离为( ).
到该椭圆左准线的距离为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.若![]() ,且
,且![]() 与
与![]() 的图象关于直
的图象关于直
线![]() 对称,则
对称,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.若向量![]() 、
、![]() 满足
满足![]() ,且
,且![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( ).
的取值范围是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.二项式![]() 的展开式中的
的展开式中的![]() 的系数是
的系数是![]() ,则
,则![]()
![]() .
.
14.设![]() ,变量满足条件
,变量满足条件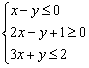 或
或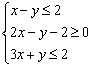 ,若使
,若使![]() 取得最小值的点
取得最小值的点![]() 有且仅有两个,则
有且仅有两个,则![]()
![]() .
.
15.在棱长均相等的正三棱柱![]() 中,
中,![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
16.设数列![]() 满足
满足![]() ,且
,且![]() ,则
,则![]()
![]() .
.
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)已知函数![]() ,求
,求![]() 的取值范围.
的取值范围.
18.(本小题满分12分)某商家进行促销活动,促销方案是:顾客每消费![]() 元,便可以获得奖券一张,每张奖券中奖的概率为
元,便可以获得奖券一张,每张奖券中奖的概率为![]() ,若中奖则商家返还顾客现金
,若中奖则商家返还顾客现金![]() 元.小王购买一套价格为
元.小王购买一套价格为![]() 元的西服,只能得到
元的西服,只能得到![]() 张奖券,于是小王补偿
张奖券,于是小王补偿![]() 元给一同事购买一件价格为
元给一同事购买一件价格为![]() 元的便服,这样小王就得到了
元的便服,这样小王就得到了![]() 张奖券.设小王这次消费的实际支出为
张奖券.设小王这次消费的实际支出为![]() 元,试分析小王出资
元,试分析小王出资![]() 元增加
元增加![]() 张奖券是否划算?
张奖券是否划算?
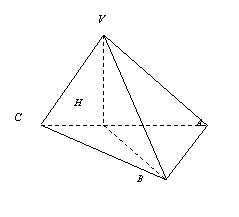 19.(本小题满分12分)在三棱锥
19.(本小题满分12分)在三棱锥![]() 中,底面
中,底面![]() 是以
是以![]() 为直角的等腰三角形.又
为直角的等腰三角形.又![]() 在底面
在底面![]() 上的射影
上的射影![]() 在线段
在线段![]() 上且靠近点
上且靠近点![]() ,
,![]() ,
,![]() ,
,
![]() 和底面
和底面![]() 所成的角为
所成的角为![]() .
.
(Ⅰ)求点![]() 到底面
到底面![]() 的距离;
的距离;
(Ⅱ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知一列非零向量![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)证明:数列![]() 是等比数列;
是等比数列;
(Ⅱ)设![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
21.(本小题满分12分)如图,点![]() 为双曲线
为双曲线![]() 的左焦点,左准线
的左焦点,左准线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 上一点.
上一点.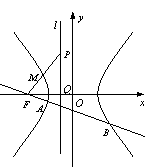 已知
已知![]() ,且线段
,且线段![]() 的中点
的中点![]() 在双曲线
在双曲线![]() 的左支上.
的左支上.
(Ⅰ)求双曲线![]() 的标准方程;
的标准方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左、右两支分别交于
的左、右两支分别交于![]() 、
、![]() 两点,
两点,
设![]() ,当
,当![]() 时,求直线
时,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
22.(本小题满分14分) 已知函数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
高考数学模拟示范卷(二)
参考答案
一.选择题(本大题12个小题,每小题5分,共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | B | C | C | B | C | C | D | B | A |
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13. ![]() 14.
14. ![]() 15.
15. ![]() 16.
16. ![]()
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)已知函数![]() ,求
,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)由![]() ,得
,得![]() ,即
,即![]() .
.
∵![]() ,∴
,∴![]() .
.
(Ⅱ)![]() ,∴
,∴![]()
![]() .∵
.∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
18.(本小题满分12分)某商家进行促销活动,促销方案是:顾客每消费![]() 元,便可以获得奖券一张,每张奖券中奖的概率为
元,便可以获得奖券一张,每张奖券中奖的概率为![]() ,若中奖则商家返还顾客现金
,若中奖则商家返还顾客现金![]() 元.小王购买一套价格为
元.小王购买一套价格为![]() 元的西服,只能得到
元的西服,只能得到![]() 张奖券,于是小王补偿
张奖券,于是小王补偿![]() 元给一同事购买一件价格为
元给一同事购买一件价格为![]() 元的便服,这样小王就得到了
元的便服,这样小王就得到了![]() 张奖券.设小王这次消费的实际支出为
张奖券.设小王这次消费的实际支出为![]() 元,试分析小王出资
元,试分析小王出资![]() 元增加
元增加![]() 张奖券是否划算?
张奖券是否划算?
解:![]() 的可能取值为
的可能取值为![]() .
.![]() ,
,![]() ,
,
![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
∴![]() 的分布列为
的分布列为
![]() (元). 同理设小王不出资
(元). 同理设小王不出资![]() 元
元
增加![]() 张奖券消费的实际支出为
张奖券消费的实际支出为![]() 元,
元,![]() .
.
![]() ,故小王出资
,故小王出资![]() 元增加
元增加![]() 张奖券划算.
张奖券划算.
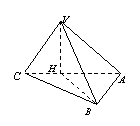 19.(本小题满分12分)在三棱锥
19.(本小题满分12分)在三棱锥![]() 中,底面
中,底面![]() 是以
是以![]() 为直角的等腰三角形.又
为直角的等腰三角形.又![]() 在底
在底
面![]() 上的射影
上的射影![]() 在线段
在线段![]() 上且靠近点
上且靠近点![]() ,
,![]() ,
,![]() ,
,
![]() 和底面
和底面![]() 所成的角为
所成的角为![]() .
.
(Ⅰ)求点![]() 到底面
到底面![]() 的距离;
的距离;
(Ⅱ)求二面角![]() 的大小.
的大小.
解:(Ⅰ)∵![]() 在底面
在底面![]() 上的射影
上的射影![]() 在线段
在线段![]() 上且靠近点
上且靠近点![]() ,
,
∴![]() 底面
底面![]() .连
.连![]() ,则
,则![]() .设
.设![]() ,
,![]() 为
为![]() 的中点,
的中点,
则![]() ,
,![]() .∴在
.∴在![]() 中,
中,![]() .在
.在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,解得
,解得![]() .故点
.故点![]() 到底面
到底面![]() 的距离为
的距离为![]() .
.
(Ⅱ)∵![]() ,∴
,∴![]() .过
.过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() 为二面角
为二面角
![]() 的平面角.∵
的平面角.∵![]() ,∴
,∴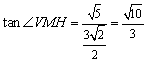 ,
,
∴二面角![]() 的大小为
的大小为![]() .
.
20.(本小题满分12分)
已知一列非零向量![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)证明:数列![]() 是等比数列;
是等比数列;
(Ⅱ)设![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
(Ⅰ)证明:![]() ,
,
∴![]() ,且
,且![]() ,∴数列
,∴数列![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(Ⅱ)解:∵![]() ,
,
∴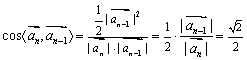 ,∴
,∴![]() ,∴
,∴![]() .
.
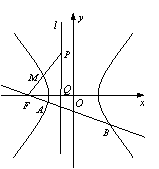 即
即![]() .
.
21.如图,点![]() 为双曲线
为双曲线![]() 的左焦点,左准线
的左焦点,左准线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]()
是![]() 上一点.已知
上一点.已知![]() ,且线段
,且线段![]() 的中点
的中点![]() 在双曲
在双曲
线![]() 的左支上.
的左支上.
(Ⅰ)求双曲线![]() 的标准方程;
的标准方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左、右两支分别交于
的左、右两支分别交于![]() 、
、![]() 两
两
点,设![]() ,当
,当![]() 时,求直线
时,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
解:(Ⅰ)设双曲线的方程为![]() ,则
,则![]() ①,
①,
![]() ,∴
,∴![]() ②.又
②.又![]() 在双曲线上,
在双曲线上,
∴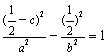 ③.由①②③解得,
③.由①②③解得,![]() ,故双曲线的方程为
,故双曲线的方程为![]() .
.
(Ⅱ)![]() ,设
,设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,则由
,则由![]() ,得
,得
![]() ,
,![]() .由
.由![]() ,得
,得![]() .∴
.∴![]() ,
,
![]() ,
,![]() .由
.由![]() ,
,![]() ,
,![]() ,
,
消去![]() ,得
,得![]() .∵
.∵![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
∴![]() ,
,![]() .又直线
.又直线![]() 与双曲线交于两支,
与双曲线交于两支, ![]() 的
的
两根同号,∴![]() .∴
.∴![]() ,解得
,解得![]() 或
或![]() .
.
故斜率![]() 的取值范围为
的取值范围为![]() .
.
22.(本小题满分14分) 已知函数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)由题意得,![]() .由函数的定义域为
.由函数的定义域为![]() ,
,
∴![]() ,
,![]() .∴函数
.∴函数![]() 有极小值
有极小值![]() .
.
(Ⅱ)∵![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .即
.即![]() 时,
时,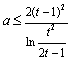 恒成立.又易证
恒成立.又易证![]() 在
在![]()
上恒成立,∴![]() 在
在![]() 上恒成立.当
上恒成立.当![]() 时取等号,
时取等号,
∴当![]() 时,
时,![]() ,∴由上知
,∴由上知![]() .故实数
.故实数![]() 的取值范围是
的取值范围是![]() .
.