高考数学模拟示范卷(三)
江西金太阳教育研究所数学研究室 编
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
1.复数![]() 的实部为( ).
的实部为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知函数![]() 的反函数
的反函数![]() 的图象经过一个定点,则这个定点的坐
的图象经过一个定点,则这个定点的坐
标为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 是( ).
是( ).
A.最小正周期为![]() 的偶函数
B.最小正周期为
的偶函数
B.最小正周期为![]() 的奇函数
的奇函数
C.最小正周期为![]() 的偶函数
D.最小正周期为
的偶函数
D.最小正周期为![]() 的偶函数
的偶函数
4.若![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() 的值为( ).
的值为( ).
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若点![]() 在以
在以![]() 为顶点的
为顶点的![]() 的内部运动(不包含边界),则
的内部运动(不包含边界),则![]() 的取值范围( ).
的取值范围( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知椭圆![]() ,顺次连结椭圆
,顺次连结椭圆![]() 的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率
的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
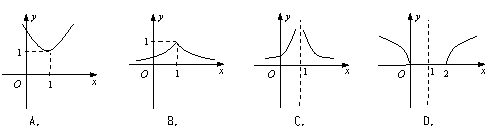 7.若实数
7.若实数![]() 满足
满足![]() ,则
,则![]() 关于
关于![]() 的函数的图象大致是( ).
的函数的图象大致是( ).
8.四面体![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,面
,面![]() 与面
与面![]() 所成的二面角为
所成的二面角为![]() ,则四面体的体积为( ).
,则四面体的体积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() ,满足
,满足![]() ,
,![]() ,则有( ).
,则有( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.从由正数组成的集合![]() 中随机地选出一个数字,且选取数字
中随机地选出一个数字,且选取数字![]() 的概率为
的概率为![]() ,下面给出四个集合:①
,下面给出四个集合:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则能当成集合的个数为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.若方程![]() (
(![]() 为常数,
为常数,![]() ),则下列判断正确的是( ).
),则下列判断正确的是( ).
A.当![]() 时,没有实根
B.当
时,没有实根
B.当![]() 时,有一个实根
时,有一个实根
C.当![]() 时,有三个实根
D.当
时,有三个实根
D.当![]() 时,有两个实根
时,有两个实根
12.用![]() ,
,![]() 分别表示
分别表示![]() 中的最大与最小者,有下列结论:
中的最大与最小者,有下列结论:
①![]() ;
;
②![]()
![]() ;
;
③若![]() ,则
,则![]() ;
;
④若![]() ,
,
则![]() .其中正确结论的个数是( ).
.其中正确结论的个数是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.![]() 的展开式中所有奇次项系数的和为
的展开式中所有奇次项系数的和为![]() .
.
14.函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
15.在圆![]() 内,过点
内,过点![]() 有
有![]() 条弦的长度成等差数列,最短弦长为数列的首项
条弦的长度成等差数列,最短弦长为数列的首项![]() ,最长弦为
,最长弦为![]() ,若公差
,若公差![]() ,则
,则![]() 的取值集合为
的取值集合为![]() .
.
16.给出下列命题:①函数![]() 与
与![]() 是同一个函数;②在
是同一个函数;②在![]() 中,若
中,若![]() ,则
,则![]() ;③
;③![]() ;④随机变量
;④随机变量![]() ,若
,若![]() ,则
,则![]() .其中正确命题的序号为
.其中正确命题的序号为![]() .(填所有正确命题的序号)
.(填所有正确命题的序号)
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知函数![]() 的反函数为
的反函数为![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的取值集合
的取值集合![]() ;
;
(Ⅱ)设函数![]() ,当
,当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
18.(本小题满分12分)(Ⅰ)在![]() 中,若
中,若![]() ,求角
,求角![]() 的大小.
的大小.
(Ⅱ)对于(Ⅰ)中的角![]() ,函数
,函数![]() 的图象按向量
的图象按向量![]() 平移后,对应的函数为偶函数,求
平移后,对应的函数为偶函数,求![]() 取最小值时的向量
取最小值时的向量![]() .
.
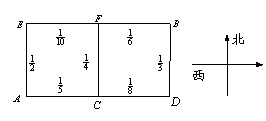 19.(本小题满分12分)某人居住在城镇的
19.(本小题满分12分)某人居住在城镇的![]() 处,准备开车到单位
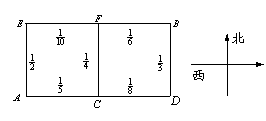
处,准备开车到单位![]() 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
![]() 算作两个路段:路段
算作两个路段:路段![]() 发生堵车事件
发生堵车事件
的概率为![]() ,路段
,路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ).
).
(Ⅰ)请你为其选择一条由![]() 到
到![]() 的最短路线(即此人只
的最短路线(即此人只
选择从西向东和从南向北的路线),使得途中发生
堵车事件的概率最小;
(Ⅱ)若记路线![]() 中遇到堵车次数为随机变量
中遇到堵车次数为随机变量![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
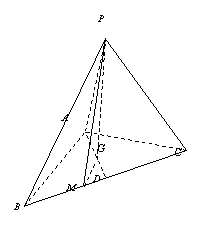 20.(本小题满分12分)已知三棱锥
20.(本小题满分12分)已知三棱锥![]() 中,
中,![]() 在底面
在底面![]() 上的射影
上的射影![]() 为
为![]() 的重心,且
的重心,且![]() .
.
(Ⅰ)求![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)当二面角![]() 的大小最小时,求三棱锥
的大小最小时,求三棱锥![]() 的体积.
的体积.
21.(本小题满分12分) 已知椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(
两点(![]() 均异于点
均异于点![]() ),且有
),且有![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点.
过定点.
22.(本小题满分14分)已知函数![]() 关于点
关于点![]() 成中心对称,且
成中心对称,且![]() .
.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)设数列![]() 满足条件:
满足条件:![]() ,
,![]() .
.
求证:![]() .
.
高考数学模拟示范卷(三)
参考答案
江西金太阳教育研究所数学研究室 编
一.选择题(本大题12个小题,每小题5分,共60分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | B | D | A | B | B | A | C | A | D | B |
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.![]() 14.
14.![]() 15.
15.![]() 16.②
16.②
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知函数![]() 的反函数为
的反函数为![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的取值集合
的取值集合![]() ;
;
(Ⅱ)设函数![]() ,当
,当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
解:(Ⅰ)![]() ,
,![]() .又
.又![]() ,∴
,∴![]() .
.
∴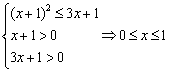 ,故集合
,故集合![]() .
.
(Ⅱ)由(Ⅰ),![]() .设
.设![]() ,则
,则![]() 为增函数.
为增函数.
∵![]() ,∴
,∴![]() ,即
,即![]() .故函数
.故函数![]() 的值域为
的值域为![]() .
.
18.(本小题满分12分)(Ⅰ)在![]() 中,若
中,若![]() ,求角
,求角![]() 的大小.
的大小.
(Ⅱ)对于(Ⅰ)中的角![]() ,函数
,函数![]() 的图象按向量
的图象按向量![]() 平移后,对应的函数为偶函数,
平移后,对应的函数为偶函数,
求![]() 取最小值时的向量
取最小值时的向量![]() .
.
解:(Ⅰ)∵![]() ,∴
,∴![]() .∵
.∵![]() 为三角形的内角,∴
为三角形的内角,∴![]() .
.
(Ⅱ)![]() .设
.设![]() ,则按向量
,则按向量![]() 平移后得,
平移后得,![]() .
.
当此函数为偶函数时,有![]() ,∴
,∴![]() .又
.又![]() 最小,
最小,
∴![]() ,故
,故![]() .
.
19.(本小题满分12分)某人居住在城镇的![]() 处,准备开车到单位
处,准备开车到单位![]() 处上班,若该地各路段发生堵车事
处上班,若该地各路段发生堵车事
 件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
![]() 算作两个路段:路段
算作两个路段:路段![]() 发生堵车事件
发生堵车事件
的概率为![]() ,路段
,路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ).
).
(Ⅰ)请你为其选择一条由![]() 到
到![]() 的最短路线(即此人只
的最短路线(即此人只
选择从西向东和从南向北的路线),使得途中发生
堵车事件的概率最小;
(Ⅱ)若记路线![]() 中遇到堵车次数为随机变量
中遇到堵车次数为随机变量![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
解:(Ⅰ)由![]() 到
到![]() 的最短路线有
的最短路线有![]() 条,即为:
条,即为:![]() ,
,![]() ,
,![]() .
.
![]() ;
;![]() ;
;
![]() .故路线
.故路线![]() 发生堵车事件的概率最小.
发生堵车事件的概率最小.
(Ⅱ)路线![]() 中遇到堵车次数
中遇到堵车次数![]() 可取值为
可取值为![]() .
.![]() ;
;
![]() ;
;![]() ;
;
![]() . 故
. 故![]() .
.
 20.(本小题满分12分)已知三棱锥
20.(本小题满分12分)已知三棱锥![]() 中,
中,![]() 在底面
在底面![]() 上的射影
上的射影![]() 为
为
![]() 的重心,且
的重心,且![]() .
.
(Ⅰ)求![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)当二面角![]() 的大小最小时,求三棱锥
的大小最小时,求三棱锥![]() 的体积.
的体积.
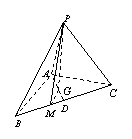
解:(Ⅰ)如图,连![]() 并延长交
并延长交![]() 于点
于点![]() ,依题意知,
,依题意知,![]() 就是
就是![]() 与底
与底
面![]() 所成的角,且
所成的角,且![]() 为
为![]() 的中点.∴
的中点.∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,故
,故![]() 与底面
与底面![]() 所成的角
所成的角![]() .
.
(Ⅱ)过点![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,斜边
中,斜边![]() 上的高为
上的高为![]() ,∴
,∴![]() .
.
在![]() 中,
中,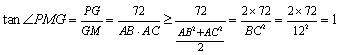 .∴二面角
.∴二面角![]()
的最小值为![]() ,当且仅当
,当且仅当![]() .∴
.∴![]() .
.
21.(本小题满分12分) 已知椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 与
与
椭圆![]() 交于
交于![]() 两点(
两点(![]() 均异于点
均异于点![]() ),且有
),且有![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点.
过定点.
(Ⅰ)解:易知![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,![]() .故方程为
.故方程为![]() .
.
(Ⅱ)证明:设![]() :
:![]() 与椭圆
与椭圆![]() 的方程联立,消去
的方程联立,消去![]() 得,
得,![]() .
.
设![]() ,则
,则![]() .
.![]()
![]()
![]()
![]() ,
,
∴![]() .若
.若![]() ,则
,则![]() :
:![]() ,
,
∴直线![]() 过定点
过定点![]() .若
.若![]() ,则
,则![]() :
:![]() ,∴直线
,∴直线![]() 过定点
过定点![]() ,
,
即为![]() 点(舍去).若斜率
点(舍去).若斜率![]() 不存在,易知
不存在,易知![]() ,符合题意. 综上,直线
,符合题意. 综上,直线![]() 过定点
过定点![]() .
.
22.(本小题满分14分)已知函数![]() 关于点
关于点![]() 成中心对称,且
成中心对称,且![]() .
.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)设数列![]() 满足条件:
满足条件:![]() ,
,![]() .
.
求证:![]() .
.
(Ⅰ)解:由题意,![]() ,即
,即![]() ,∴
,∴![]()
![]() 对一切实数
对一切实数![]() 恒成立.得
恒成立.得![]() ,又由
,又由![]() 得
得![]() ,
,
![]() .故函数
.故函数![]() 的表达式为
的表达式为![]() .
.
(Ⅱ)证明:![]() ,∴
,∴![]() .令
.令![]() ,
,
则![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
故![]()
![]() .
.