高考数学模拟考试 (一)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,
考试用时120分钟。
第Ⅰ卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题意要求的.
1.“![]() ”是“
”是“![]() ”的
( )
”的
( )
![]() 充分不必要条件
充分不必要条件 ![]() 必要不充分条件
必要不充分条件 ![]() 充要条件
充要条件 ![]() 既不充分也不必要条件
既不充分也不必要条件
2.若二项式![]() 的展开式中含
的展开式中含![]() 的项是第8项,则正整数
的项是第8项,则正整数![]() 的值为( )
的值为( )
![]()
![]()
![]()
![]()
3.已知函数![]() 的图象与直线
的图象与直线![]() 的交点中,距离最近两点的距离为
的交点中,距离最近两点的距离为![]() 则
则![]() ( )
( )
![]()
![]()
![]()
![]()
4.已知方程![]() =1的图象是双曲线,则m的取值范围是
( )
=1的图象是双曲线,则m的取值范围是
( )
![]()
![]()
![]()
![]() 或
或![]()
5.已知函数![]() 的反函数为
的反函数为![]() 则 (
)
则 (
)
![]()
![]()
![]()
![]()
6.互不相等的三个正数![]() 成等比数列,且点
成等比数列,且点![]()
![]() ,
,![]() 共线(
共线(![]() ),则
),则![]() 成 ( )
成 ( )
![]() 等差数列,但不成等比数列
等差数列,但不成等比数列
![]() 等比数列而非等差数列
等比数列而非等差数列
![]() 等比数列,也可能成等差数列
等比数列,也可能成等差数列
![]() 既不是等比数列,又不是等差数列
既不是等比数列,又不是等差数列
7.把直线![]() 绕原点逆时针方向转动,使它与圆
绕原点逆时针方向转动,使它与圆![]() 相切,则直线转动的最小正角是
( )
相切,则直线转动的最小正角是
( )
![]()
![]()
![]()
![]()
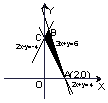
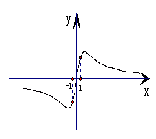 8.若函数
8.若函数![]() 的图象如右,则
的图象如右,则![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
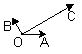 9.如图,在平面内有三个向量
9.如图,在平面内有三个向量![]() 满足
满足![]() 与
与![]() 的夹角为
的夹角为![]() 与
与![]() 的夹角为
的夹角为![]() 设
设![]() 则
则![]() 的值为( )
的值为( )
![]()
![]()
![]()
![]()
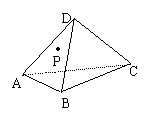 |
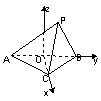
10.如图正四面体D-ABC中, P∈面DBA, 则在平面DAB内过点P与
直线BC成60°角的直线共有 ( )
A.0条 B.1条 C.2条 D.3条
11.函数y=2sinxsin2x的最大值是 ( )
A.![]() B.
B.![]() C.2
C.2![]() D.
D.![]()
12.已知函数![]() 满足:对任意实数
满足:对任意实数![]() ,当
,当![]() 时,总有
时,总有![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
第II卷(非选择题,90分)
二、填空题(本题满分16分,每小题4分,共4个小题。请将答案直接填入题后的横线中)
13.某学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .
14.已知实数![]() 满足
满足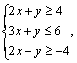 则
则![]() 的取值范围为
.
的取值范围为
.
15.考察下列三个命题,是否需要在“ ”添加一个条件,才能构成真命题(其中![]() 为直线,
为直线,![]() 为平面)?如需要,请填上所添条件,如不需要,请将“ ”划掉。
为平面)?如需要,请填上所添条件,如不需要,请将“ ”划掉。
(1)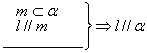 (2)
(2)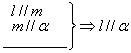 (3)
(3)![]()
16.曲线![]() 的两条切线
的两条切线![]() 都过点
都过点![]() ,若两切线
,若两切线![]() 的夹角为
的夹角为![]()
则![]() 。
。
三、解答题(本大题共6个小题,共74分。解答应写出文字说明,推证步骤或演算过程)
17.(12分)已知函数![]() (1)当
(1)当![]() 时,求函数
时,求函数![]() 的值域;(2)将函数
的值域;(2)将函数![]() 的图象按向量
的图象按向量![]() 平移,使得平移后的函数
平移,使得平移后的函数![]() 的图象关于直线
的图象关于直线![]() 对称,求函数
对称,求函数![]() 的单调递增区间。
的单调递增区间。
18.(12分)盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,每张卡片被抽出的可能性都相等,求: (Ⅰ)抽出的3张卡片上最大的数字是4的概率; (Ⅱ)抽出的3张中有2张卡片上的数字是3的概念;(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
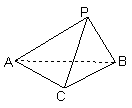 19.(12分)如图,已知三棱锥
19.(12分)如图,已知三棱锥![]() 中,
中,![]() 平面
平面![]() 平面
平面![]()
![]() (1)求二面角
(1)求二面角![]() 的大小;(2)若
的大小;(2)若![]() 为棱
为棱![]() 上的一动点,则直线
上的一动点,则直线![]() 与底面
与底面![]() 能否成
能否成![]() 的角?若能,求出点
的角?若能,求出点![]() 的位置;若不能,说明理由。
的位置;若不能,说明理由。
20.(12分)已知数列![]() 的前
的前![]() 项和
项和![]() 且
且![]() 是
是![]() 和
和![]() 的等差中项。(1)求数列
的等差中项。(1)求数列![]() 和
和![]() 的通项公式;(2)若
的通项公式;(2)若![]() 求
求![]() ;(3)若
;(3)若![]() 是否存在
是否存在![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
21.(本小题满分13分)已知函数f(x)=-x3+ax2+b的图象上任意两点连线的斜率都小于1.
(Ⅰ)判断函数g(x)=f(x)-x的单调性,并加以证明;
(Ⅱ)求实数a的取值范围.
22、(本小题满分13分)已知椭圆C:![]() +
+![]() =1(a>b>0)的左、右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴、y轴分别交于点A、B ,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左、右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴、y轴分别交于点A、B ,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设![]() =λ
=λ![]() .
.
(Ⅰ)证明:λ=1- e2;
(Ⅱ)若![]() ,△PF1F2的周长为6;写出椭圆C的方程.
,△PF1F2的周长为6;写出椭圆C的方程.
高考模拟试卷(一)答案
一、选择题解答及答案:
1.选![]() 但是,
但是,![]() 可能为
可能为![]() 不能得到
不能得到![]()
2.选![]() 由已知:
由已知:![]()
3.选![]() 令
令![]() 然后代入检验即可.
然后代入检验即可.
4.选![]() 由已知:
由已知:![]() 或
或![]()
5.选![]() 对任意的实数
对任意的实数![]() 恒成立,
恒成立,![]() 函数
函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,![]() 即:
即:![]() 在定义域
在定义域![]() 上单调递减,
上单调递减,![]() 排除选项
排除选项![]() 选
选![]()
6选![]() 令
令![]() 的公比为
的公比为![]() 且
且![]() 由已知:
由已知: ![]()
![]()
![]() 同理:
同理: ![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 既成等比数列又成等差数列,否则,仅成等比数列.
既成等比数列又成等差数列,否则,仅成等比数列.
7选![]() 把圆方程配方为:
把圆方程配方为:![]() 圆心
圆心![]() 半径
半径![]() 又
又![]() 直线
直线![]()
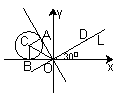
![]() 的倾角为
的倾角为![]() 作出图形, 在
作出图形, 在![]() 中,
中, ![]()
![]()
![]()
![]() ,
,![]() .故选
.故选![]()
8. 解答 B.![]() 时
时![]() .因为函数的定义域为R,即
.因为函数的定义域为R,即![]() 恒不等于零,
恒不等于零,![]() .又在
.又在![]() 上函数
上函数![]() 在
在![]() 处取得最大值,而
处取得最大值,而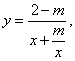
![]() .综上
.综上![]() ,故选择B.
,故选择B.
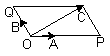 9.选
9.选![]() 如图,以
如图,以![]() 为对角线,作平行四边形,使其它两边所在直线平行于直线
为对角线,作平行四边形,使其它两边所在直线平行于直线![]() 由题意:
由题意:![]() 在
在![]() 中,
中,![]()
![]()
10. 选C、在平面DAB内过点B与直线BC成60°角的直线共有2条,
故在平面DAB内过点P与直线BC成60°角的直线共有2条。
11. 选B ![]()
≤![]() ,
,
当且仅当![]() 时取“=”.
时取“=”.
12.选 D.由题意知函数![]() 在区间
在区间![]() 上是减函数,又
上是减函数,又![]() 在区间
在区间![]() 上也是减函数,
上也是减函数,![]() ,解得
,解得![]() ,故选择D.
,故选择D.
二、填空题解答及答案
13.150.![]() 教师与学生所抽取的人数之比为
教师与学生所抽取的人数之比为![]() 教师人数为
教师人数为![]()
 14.
14.![]() 。作出约束条件的可行域如右图的
。作出约束条件的可行域如右图的![]() 内部,包括边界。令
内部,包括边界。令![]() 则问题转化为:直线
则问题转化为:直线![]() 与可行域有公共点,相当于该直线与线段
与可行域有公共点,相当于该直线与线段![]() 相交,可求出点
相交,可求出点![]() ,
,![]() 解之得:
解之得:![]()
15.(1)![]() ,(2)
,(2) ![]() ,(3)
,(3)![]() 。
。
16.![]() 。设切点
。设切点![]() 坐标为
坐标为![]() 过切点
过切点![]() 的切线方程为:
的切线方程为:
![]() 切线过点
切线过点![]()
![]()
![]() 或
或![]() 解之得:
解之得:![]() 或
或![]()
![]() 切线
切线![]() 的斜率分别为:
的斜率分别为:![]()
三、解答题答案
17.解: ![]()
![]()
(1)![]()
![]()
![]()
![]() 函数
函数![]() 的值域为
的值域为![]()
(2)函数![]() 的图象按向量
的图象按向量![]() 平移后的解析式为:
平移后的解析式为:![]() 即:
即:
![]() 其图象的对称轴方程都可表示为:
其图象的对称轴方程都可表示为:![]()
![]() 又
又![]() 该图象关于直线
该图象关于直线![]() 对称,
对称,![]()
![]() 令
令![]()
![]() 解之得:
解之得: ![]() 函数
函数![]() 的单调递增区间为:
的单调递增区间为:![]()
18. 解:(I)“抽出的3张卡片上最大的数字是4”的事件记为A,由题意
![]()
(II)“抽出的3张中有2张卡片上的数字是3”的事件记为B,则![]()
(III)“抽出的3张卡片上的数字互不相同”的事件记为C,“抽出的3张卡片上有两个数字相同”的事件记为D,由题意,C与D是对立事件,因为![]()
 所以
所以![]() .
.
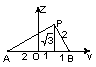 19.(1) 取
19.(1) 取![]() 的中点
的中点![]() 连接
连接![]() .则
.则![]() 面
面![]() 面
面![]() 面
面![]() 以点
以点![]() 为原点,建立空间直角坐标系如图.(在立体图形中取出部分平面图形)易得:点
为原点,建立空间直角坐标系如图.(在立体图形中取出部分平面图形)易得:点![]() 易得:向量
易得:向量![]() 面
面![]() ;设向量
;设向量
![]() 面
面![]() 则
则![]()
![]()
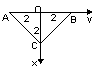
![]()
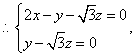 解之得:
解之得: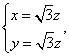 令
令![]() 则:
则:![]()
![]()
![]()
![]()
![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]()
(2)设点![]() 分线段
分线段![]() 之比为
之比为![]() 则点
则点![]() 的坐标为
的坐标为![]()
![]()
![]() 由题意:
由题意:![]()
![]()
![]()
![]() 化简得:
化简得:![]() 满足条件的实数
满足条件的实数![]() 不存在。
不存在。![]() 棱
棱![]() 上不存在满足条件的点
上不存在满足条件的点![]()
20.(1)当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
![]()
又![]() 是
是![]() 和
和![]() 的等差中项,
的等差中项,![]()
(2)![]()
![]()
![]()
……………
![]()
以上![]() 个等式叠加得:
个等式叠加得:![]()
(3)当![]() 为奇数时,
为奇数时,![]()
由已知:![]()
当![]() 为偶数时,
为偶数时,![]()
由已知:![]()
综上,满足条件的正自然数![]() 不存在。
不存在。
21.(Ⅰ)设f(x)上任意两点A(x1,f(x1)),B(x2,f(x2)).不妨令x1>x2.∵![]() ,
,
∴f(x1)-f(x2)<x1-x2,即f(x1)-x1<f(x2)-x2,令g(x)=f(x)-x=-x3+ax2-x+b,∵当x1>x2时,
g(x1)<g(x2),∵g(x)单调递减.
(Ⅱ)∴g(x)单调递减,∴![]() 恒成立,∴-3x2+2ax-1≤0恒成立,∴△=4a2-12≤0,
恒成立,∴-3x2+2ax-1≤0恒成立,∴△=4a2-12≤0,
∴-![]() ≤a≤
≤a≤![]() .
.
(22) (Ⅰ)证法一:因为A、B分别是直线l:![]() 与x轴、y轴的交点,
与x轴、y轴的交点,
所以A、B的坐标分别是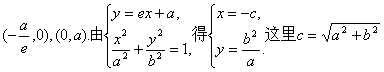 .
.
所以点M的坐标是(![]() ). 由
). 由![]()
即
证法二:因为A、B分别是直线l:![]() 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是![]() 设M的坐标是
设M的坐标是![]()
所以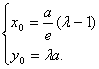 因为点M在椭圆上,所以
因为点M在椭圆上,所以 ![]()
即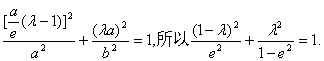
![]() 解得
解得![]()
(Ⅱ)当![]() 时,
时,![]() ,所以
,所以![]() 由△MF1F2的周长为6,得
由△MF1F2的周长为6,得![]()
所以![]() 椭圆方程为
椭圆方程为![]()