高考数学模拟考试试卷
理科数学
一、选择题:(每小题5分,共50分)
1.设复数![]() 满足关系式
满足关系式![]() ,那么
,那么![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的值是
的值是
A.15 B.22 C.31 D.64
3.若命题![]() :
:![]() ,则
,则![]() 是
是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
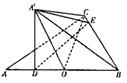
 4.一植物园参观路径如右图所示,若要全部参观并且路线不重复,则不同
4.一植物园参观路径如右图所示,若要全部参观并且路线不重复,则不同
的参观路线种数共有
A. 6种 B. 8种 C. 36种 D. 48种
5.已知空间直角坐标系![]() 中有一点
中有一点![]() ,点
,点![]() 是
是![]() 平面内的直线
平面内的直线
![]() 上的动点,则
上的动点,则![]() 两点的最短距离是
两点的最短距离是
A.![]() B.
B. ![]() C.3
D.
C.3
D.![]()
6.若不等式![]() 对任意正整数
对任意正整数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
7.点![]() 在由不等式组
在由不等式组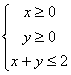 确定的平面区域内,
确定的平面区域内,![]()
![]() 所在平面
所在平面
区域的面积是
A. 1 B. 2 C. 4 D.8
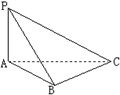 8.如图,三棱锥
8.如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球表面积为
的外接球表面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.设![]() 是
是![]() 内任一点,且
内任一点,且![]() 设
设![]() 的面积分别为
的面积分别为![]() ,且
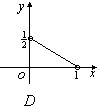
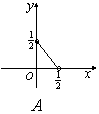
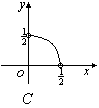
,且![]() ,则在平面直角中坐标系中,以
,则在平面直角中坐标系中,以![]() 为坐标的点
为坐标的点![]() 的轨迹图形是
的轨迹图形是
 | |||||||
 | 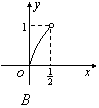 |  | |||||
10.对于集合![]() 、
、![]() , 定义
, 定义![]() ,
,![]() ,设集合
,设集合![]() ,
,![]() ,则
,则![]() 等于
等于
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二、填空题(每小题5分,共25分)
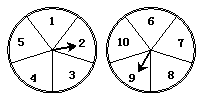 11.如图所示两个带指针的转盘,每个转盘被分成5个
11.如图所示两个带指针的转盘,每个转盘被分成5个
区域,指针落在5个区域的可能性相等,每个区域
内标有一个数字,则两个指针同时落在奇数所在区
域内的概率为 .
12.函数![]() 在
在![]() 上的最大值为
.
上的最大值为
.
13.设![]() ,则
,则![]() .
.
14.点![]() 是双曲线
是双曲线![]() 和圆
和圆![]() 的一个交点,且
的一个交点,且![]() ,其中
,其中![]() 是双曲线
是双曲线![]() 的两个焦点,则双曲线
的两个焦点,则双曲线![]() 的离心率为
。
的离心率为
。
15.函数![]() (其中
(其中![]() ),
),![]() 是
是![]() 的小数点后第
的小数点后第![]() 位数字,
位数字,![]() ,
,
则![]() 的值为
的值为
三、解答题(本大题共6小题,共75分)
16.(本小题满分12分)
已知函数![]() 的图象(部分)如图所示,
的图象(部分)如图所示,
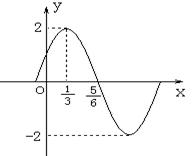 (1)试确定
(1)试确定![]() 的解析式;
的解析式;
(2)若![]() 求
求![]() 的值。
的值。
17.(本小题满分12分)
抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列![]() ,使
,使
 ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,求
,求![]() 的概率.
的概率.
18.(本小题满分12分)
| |
△![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 成30°角.
成30°角.
(1)若点![]() 到直线
到直线![]() 的距离为1,求二面角
的距离为1,求二面角![]() 的大小;
的大小;
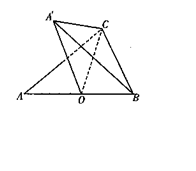 (2)若
(2)若![]() ,求
,求![]() 边的长.
边的长.
19.(本小题满分12分)
已知函数![]() 在
在![]() 上最小值是
上最小值是![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:![]() ;
;
(3)在点列![]() 中是否存在两点
中是否存在两点![]() ,使直线
,使直线![]() 的斜率为1?若存在,求出所有的数对
的斜率为1?若存在,求出所有的数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
20.(本小题满分13分)
某水库年初的存水量为![]() ,其中污染物的含量为
,其中污染物的含量为![]() ,该年每月降入水库的
,该年每月降入水库的
水量与月份![]() 的关系是
的关系是![]() (
(![]() ),且每月流入水库的污水
),且每月流入水库的污水
量![]() ,其中污染物的含量为
,其中污染物的含量为![]() ,又每月库水的蒸发量也为
,又每月库水的蒸发量也为![]() (假设水与污染物能充
(假设水与污染物能充
分混合,且污染物不蒸发,该年水库中的水不作它用).
(1)求第![]() 个月水库含污比
个月水库含污比![]() 的表达式(含污比
的表达式(含污比![]() );
);
(2)当![]() 时,求水质最差的月份及此月份的含污比.
时,求水质最差的月份及此月份的含污比.
21.(本小题满分14分)
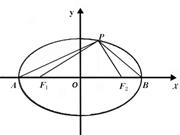
如图,已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 和
和![]() ,椭圆
,椭圆![]() 与
与![]() 轴的两交点分别为A、B,点P是椭圆上一点(不与点A、B重合),且∠APB=
轴的两交点分别为A、B,点P是椭圆上一点(不与点A、B重合),且∠APB=![]() ,∠F1PF2
,∠F1PF2![]() .
.
 (1)若
(1)若![]() ,三角形F1PF2的面积为
,三角形F1PF2的面积为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)当点![]() 在椭圆
在椭圆![]() 上运动,试证明
上运动,试证明![]() 为定值.
为定值.
参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | D | B | A | C | A | A | C |
二、填空题:
11. ![]() ; 12.
; 12. ![]() ; 13. 128; 14.
; 13. 128; 14. ![]() 15. 2;
15. 2;
三、解答题:
16.解:(1)由图象可知![]() , ∴T=2,
, ∴T=2, ![]() …………3分
…………3分
将点P(![]() )代入
)代入![]() ,得
,得![]() ,又
,又 ![]() ,
,
故所求解析式为 ![]() ………………………………………6分
………………………………………6分
(2)∵![]() , ∴
, ∴![]() ,即
,即 ![]() ……………………8分
……………………8分
∴
![]()
![]()
![]() ………12分
………12分
17. 解:(1)设事件![]() 为A,则在7次抛骰子中出现5次奇数,2次偶数,
为A,则在7次抛骰子中出现5次奇数,2次偶数,
而抛骰子出现的奇数和偶数的概率为P是相等的,且为![]()
根据独立重复试验概率公式:![]() ………………………………6分
………………………………6分
(2)若![]() ,即前2次抛骰子中都是奇数或都是偶数.
,即前2次抛骰子中都是奇数或都是偶数.
若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,
其概率:![]() …………………………………………………………8分
…………………………………………………………8分
若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:
![]() …………………………………………………………………………10分
…………………………………………………………………………10分
![]() 所求事件的概率
所求事件的概率![]() …………………………………12分
…………………………………12分
18.解:(I)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.
过点A′作A′D⊥AB,垂足为D,则A′D⊥平面ABC,
∴∠A′ED=30°,又A′O=BO=1,∴∠A′OD=60°,从而A′D=A′Osin60°=![]() .
.
过点D作DE⊥BC,垂足为E,连结A′E,据三垂线定理,A′E⊥BC.
∴∠A′ED为二面角A′—BC—A的平面角.
由已知,A′E=1,在Rt△A′DE中![]()
∴∠A′ED=60°故二面角A′—BC—A的大小为60°. ………………………………6分
(II)设BC=![]() ,∠A′CB=θ,则A′C=
,∠A′CB=θ,则A′C=![]() ,∠OCB=π-θ.
,∠OCB=π-θ.
|
在△A′DB中,A′B=![]()
在△A′BC中,A′B2=A′C2+BC2-2A′C·BC![]()
![]()
![]()
![]() ………………………………………………………12分
………………………………………………………12分
19.解:(1)由![]() 得
得![]() ,令
,令![]() ,
,
当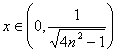 时,
时,![]() ; 当
; 当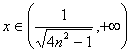 时,
时,![]() ,
,
∴![]() 在
在![]() 上,当
上,当![]() 时取得最小值
时取得最小值![]() ,∴
,∴![]() ………4分
………4分
(2)证明:∵![]()
∴![]()
………………………………………………8分
(3)不存在. 假设存在两点![]() 满足题意,即
满足题意,即![]() ,
,
令![]() ,则
,则![]() ,故点
,故点![]() 都在双曲线
都在双曲线![]() 上,
上,
而双曲线的一条渐近线方程为![]() ,其斜率为1,这显然不可能,所以这样的两点
,其斜率为1,这显然不可能,所以这样的两点![]() 不存在。………………………………………………………………………………………………12分
不存在。………………………………………………………………………………………………12分
20.解:(1)第x月水库含污染物![]() ,库容总量=
,库容总量=![]()
当![]()
此时库容量![]()
当![]()
此时,库容总量![]()
∴ 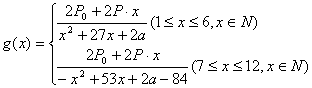 …………………………………6分
…………………………………6分
(2)∵![]() ,
,![]() ,当
,当![]() 时,
时,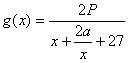
易证![]() 上是减函数,且恒大于零,
上是减函数,且恒大于零,
∴![]() 上是增函数 ∴当
上是增函数 ∴当![]() 时,
时,![]()
当![]() 时,
时,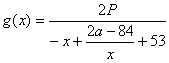
易证![]() 在
在![]() 上是减函数,且恒大于零.
上是减函数,且恒大于零.
∴![]() 上是增函数 , 当x=12时,
上是增函数 , 当x=12时,![]() .
.
∵![]() , ∴
, ∴![]() .
.
∴水质量最差的是12月份,其含污比为![]() ……………………………………13分
……………………………………13分
21.解:(Ⅰ)由于三角形F1PF2为直角三角形,则![]() ,
,
即![]() ,
,
![]() 三角形F1PF2的面积为
三角形F1PF2的面积为![]() ,∴
,∴ ![]() ,即
,即![]() ,
,
![]()
![]() ,即
,即![]() , ∴
, ∴![]() .
.
![]() 椭圆C的离心率为
椭圆C的离心率为![]() ,则
,则![]() ,即
,即![]() , ∴
, ∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .……………………………………………………7分
.……………………………………………………7分
(Ⅱ)不妨设点![]()
![]() 在第一象限,则在三角形
在第一象限,则在三角形![]() 中,
中,
![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
![]()
![]()
![]() .
.
![]()
![]() , ∴
, ∴![]() ,即
,即![]() .
.
作![]() 轴,垂足为
轴,垂足为![]() .
.
![]()
![]() ,
,![]() ,
,
∴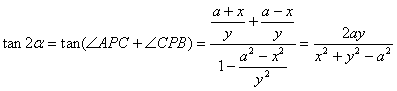 .
.
![]()
![]() , ∴
, ∴![]() . ∴
. ∴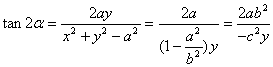 .
.
∴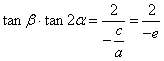 ,
,![]() 离心率
离心率![]() ,∴
,∴![]() .
.
∴![]() 是定值, 其值为
是定值, 其值为![]() . ……………………………………………………14分
. ……………………………………………………14分