高考数学模拟考试题（理科卷2）
时量120分钟 总分150分
一、选择题（每小题5分，共50分）
1．非空集合A、B满足
，U是全集，则下列式子：①
，②
，③（
）
B＝U，④（）（
）＝U中成立的是（ ）．
A．①，② B．③，④ C．①，②，③ D．①，②，③，④
2．已知
＝（3，-2），
＝（-5，-1），则
等于（ ）．
A．（8，1） B．（-8，1） C．（-8，-1） D．
，）
3．函数
的定义域是（ ）．
A．（2，3） B．[2，
C．（2，
D．（2，＋∞）
4．如果数列
的前n项和
，那么这个数列（ ）．
A．是等差数列而不是等比数列 B．是等比数列而不是等差数列
C．既是等差数列又是等比数列 D．既不是等差数列又不是等比数列
5．锐二面角
的棱l上一点A，射线
，且与棱成45°角，又AB与
成30°角，则二面角的大小是（ ）．
A．30° B．45° C．60° D．90°
6．有6个人分别来自3个不同的国家，每一个国家2人。他们排成一行，要求同一国家的人不能相邻，那么他们不同的排法有（ ）．
A．720 B．432 C．360 D．240
7．直线经过点A（2，1），B（1，
）两点
，那么直线l的倾斜角取值范围是（ ）．
A．[0，
B．
，
， C．
，
D．
，
，
8．下列函数中同时具有性质：（1）最小正周期是
，（2）图象关于
对称，（3）在
，
上是增函数的是（ ）．
A．
B．
C．
D．
9．设下表是某班学生在一次数学考试中数学成绩的分布表
| 分数 |
|
|
|
|
|
|
|
|
| 人数 | 2 | 5 | 6 | 8 | 12 | 6 | 4 | 2 |
，
，
，
，
，
，
，
那么分数在[100，110]中和分数不满110分的频率和累积频率分别是（ ）．
A．0.18，0.47 B．0.47，0.18 C．0.18，1 D．0.38，1
10．已知
，则以下选项正确的是（ ）．
A．f（3）＞f（1）＞f（2） B．f（3）＞f（1）＞f（2）
C．f（3）＞f（2）＞f（1） D．f（1）＞f（3）＞f（2）
二、填空题：本大题共5小题；每小题4分，共20分．把答案填在题中横线上
11．已知直线ax+by+1=0中的a，b是取自集合{－3，－2，－1，0，1，2}中的2个不同的元素，并且直线的倾斜角大于60°，那么符合这些条件的直线的共有
A．8条 B．11条 C．13条 D．16条
12．某学校共有学生4500名，其中初中生1500名，高中生3000名，用分层抽样法抽取一个容量为300的样本，那么初中生应抽取 名．
13．不等式(x－2)≥0的解集是 ．
14．若（1＋x＋
）10＝40i=1aix10－i，则a10＝ ．
15．给出下列四个命题：
①过平面外一点，作与该平面成θ角的直线一定有无穷多条；
②一条直线与两个相交平面都平行，则它必与这两个平面的交线平行；
③对确定的两条异面直线，过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行；
④对两条异面的直线，都存在无穷多个平面与这两条直线所成的角相等；
其中正确的命题序号为 （请把所有正确命题的序号都填上）．
三、解答题：本大题共6小题；共74分，解答应写出文字说明，证明过程或演算步骤．
16．(本题满分12分)
已知数列
满足
>0，且对一切n∈N+ ，有ni=1=，其中Sn=ni=1ai，
对一切n∈N+，有－an+1=2Sn； 求数列的通项公式；
17．（本小题满分12分）
已知向量a= (sinωx，cosωx)，b=( cosωx，cosωx)，其中ω＞0，记函数
=a·b，已知的最小正周期为π．
（Ⅰ）求ω；
（Ⅱ）当0＜x≤时，试求f(x)的值域．
18．（本小题满分12分）
对5副不同的手套进行不放回抽取，甲先任取一只，乙再任取一只，然后甲又任取一只，最后乙再任取一只．
（Ⅰ）求下列事件的概率：
①A：甲正好取得两只配对手套；
②B：乙正好取得两只配对手套；
（Ⅱ）A与B是否独立？并证明你的结论．
19．(本小题满分12分)
已知斜三棱柱ABC—A1B1C1的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α（0°＜α＜90°），点
在底面上的射影
落在
上．
（Ⅰ）求证：AC⊥平面BB1C1C；
（Ⅱ）当α为何值时，AB1⊥BC1，且使D恰为BC中点？
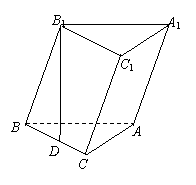（Ⅲ）若α = arccos ，且AC=BC=AA1时,求二面角C1—AB—C的大小．
20．（本小题满分12分）
已知函数f(x)=(x－a)(x－b)(x－c)．
（Ⅰ）求证：f′(x)=(x－a)(x－b)＋(x－a) (x－c)＋(x－b) (x－c)；
（Ⅱ）若f(x)是R上的增函数，是否存在点P，使f(x)的图像关于点P中心对称？如果存在，请求出点P坐标，并给出证明；如果不存在，请说明理由．
21．(本题满分12分)
已知正方形的外接圆方程为 x2+y2－24x+a=0，A、B、C、D按逆时针方向排列，正方形一边CD所在直线的方向向量为(3，1)．
（Ⅰ）求正方形对角线AC与BD所在直线的方程；
（Ⅱ）若顶点在原点，焦点在x轴上的抛物线E经过正方形在x轴上方的两个顶点A、B，求抛物线E的方程．
数学参考答案与评分标准
一、
1．C 2．D 3．A 4．B 5．B 6．D 7．B 8．C 9．A 10．A
二、填空题：本大题共5小题；每小题4分，共20分．
11.16条 12．100 13. {xx=－1或x≥3}， 14. 2101 15.（2）、（4）
三、解答题：本大题共6小题；共80分．
16． (Ⅰ)由ni=1
=Sn2， (1)
由n＋1i=1=Sn＋12，
(2)
(2)－(1)，得
=(Sn+1+Sn)(Sn+1－Sn)=(2 Sn+an+1) an+1．
∵ an+1 >0，∴an＋12－
=2Sn．
……………………………12分
17．（Ⅰ）=sinωxcosωx＋cos2ωx
…………………… 2分
=
sin2ωx＋(1+cos2ωx)
=sin(2ωx+)+ ……………………… 4分
∵ ω>0，∴T=π=，∴ω=1． ……………………… 6分
（Ⅱ）由（1），得=sin(2x+)
+ ,
∴0＜x≤, ∴＜2x+≤． ………………………… 9分
∴∈[1，]．
………………………… 12分
18． (Ⅰ)①P（A）= = ． ……………………… 4分
②
== ．
………………………
8分
(Ⅲ) P（AB）= = , 
=
，
∴≠
，故A与B是不独立的． ……………………… 14分
19. （Ⅰ）∵ B1D⊥平面ABC， AC
平面ABC，
∴ B1D⊥AC,
又AC⊥BC, 
BC∩B1D=D．
∴ AC⊥平面BB1C1C． ………………………… 3分
(Ⅱ) ∵ AC⊥平面BB1C1C ，要使AB1⊥BC1 ，由三垂线定理可知，
只须B1C⊥BC1， ………………………… 5 分
∴ 平行四边形BB1C1C为菱形， 此时，BC=BB1．
又∵ B1D⊥BC, 要使D为BC中点，只须B1C= B1B，即△BB1C为正三角形，
∴ ∠B1BC= 60°． ………………………… 7分
∵ B1D⊥平面ABC，且D落在BC上，
∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且使D为BC中点． ……………………… 8分
（Ⅲ）过C1作C1E⊥BC于E，则C1E⊥平面ABC．
过E作EF⊥AB于F，C1F，由三垂线定理，得C1F⊥AB．
∴∠C1FE是所求二面角C1—AB—C的平面角． …………………… 10分
设AC=BC=AA1=a，
在Rt△CC1E中，由∠C1BE=α=
，C1E=
a．
在Rt△BEF中，∠EBF=45°，EF=
BE=a．
∴∠C1FE=45°，故所求的二面角C1—AB—C为45°．……………… 14分
解法二：（1）同解法一 ……………… 3分
（Ⅱ）要使AB1⊥BC1，D是BC的中点，即
=0，=，
∴
， 
=0，∴
．
∴
，故△BB1C为正三角形，∠B1BC=60°；
∵ B1D⊥平面ABC，且D落在BC上， …………………… 7分
∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且D为BC中点． …………………8分
（Ⅲ）以C为原点，CA为x轴，CB为y轴，经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系，则A（a，0，0），B（0，a，0），C（0，－
，a），
平面ABC的法向量n1=（0，0，1），设平面ABC1的法向量n2=（x，y，z）．
由
n2=0，及
n2=0，得
∴n2=（
，，1）． ……………………10分
cos<n1, n2>＝= ，
故n1 , n2所成的角为45°，即所求的二面角为45°．………………………14分
20. （Ⅰ）∵ f(x)=(x－a)(x－b)(x－c)
＝ｘ3－（a+b +ｃ)x2＋(ab+bc+ac)x－abc ……………3 分
f ′(x)=3 x2－2(a+b +ｃ)x＋(ab+bc+ac)
=[ x2－ (a+b)x＋ab]＋[ x2－ (a+c)x＋ac]＋[ x2－ (b+c)x＋bc]
=(x－a)(x－b)＋(x－a)(x－c) ＋(x－b)(x－c)．……………………………6分
（Ⅱ）∵f(x)是R上的单调函数，∴f ′(x)≥0，对x∈R恒成立，
即 3x2－2(a+b+c)x+(ab+bc+ca)≥0 对x∈R恒成立．
∴△≤0, 4(a+b+c)2－12(ab+bc+ca) ≤0，
∴ (a－b)2＋(a－c）2＋ (b－c)2≤0，∴ a=b=c．
∴ f(x)=(x－a)3 ， ∴f(x)关于点(a，0)对称． ………………………9分
证明如下：设点P(x，y)是 f(x)=(x－a)3图像上的任意一点，y=(x－a)3，
点P关于点(a，0)对称的点P′(2a－x，－y)，
∵(2a－x－a)3=(2a－x)3= －(x－2a)3=－y ，
∴点P′在函数f(x)=(x－a)3的图像上，即函数f(x)=(x－a)3关于点(a，0)对称．
…………………………………………………………14分
21．(Ⅰ) 由（x－12）2+y2=144－a(a<144),
可知圆心M的坐标为(12，0)， …………………………2分
依题意，∠ABM=∠BAM=，kAB= , MA、MB的斜率k满足 =1,
解得
=2，
=－ ．
…………………………………4分
∴所求BD方程为x+2y－12=0，AC方程为2x－y－24=0． ……………6分
(Ⅱ) 设MB、MA的倾斜角分别为θ1，θ2，则tanθ1＝2，tanθ2＝－，
设圆半径为r，则A（12＋
），B（12－
，
），
……9分
再设抛物线方程为y2＝2px (p＞0)，由于A，B两点在抛物线上，
∴ ∴ r=4，p=2．
得抛物线方程为y2＝4x。 ……………………………………14分