高考数学模拟考试题3

高考数学模拟考试题（理科卷3）

时量120分钟　总分150分

 

一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．若集合M={yy=x^-2}，P={yy=}，那么M∩P=

A．(1，+∞)　　　　　　  B．［1，+∞)　　　　 C．(0，+∞)　　 D．［0，+∞)

2．设3^a=4,3^b=12,3^c=36，那么数列a，b，c

Ａ．是等差数列但不是等比数列　　　　　  B．是等比数列但不是等差数列

Ｃ．既是等差数列也是等比数列　　　　　  Ｄ．既不是等差数列也不是等比数列

3．种植两株不同的花卉，它们的存活率分别为p和q，则恰有一株存活的概率为

A．p+q－2p q　　　　　　 B．p+q－pq　　　　　　 C． p+q　　　D． pq

4．函数f(x)=sin(2x+φ)+cos(2x+φ)的图像关于原点对称的充要条件是

A．φ=2kπ－，k∈Z　　　　  　　　　B．φ=kπ－，k∈Z

C．φ=2kπ－，k∈Z　　　　　　　　  D．φ=kπ－，k∈Z

5．将棱长为3的正四面体的各棱长三等份，经过分点将原正四面体各顶点附近均截去一个棱长为1的小正四面体，则剩下的多面体的棱数E为

A．16　　　　　　　  B．17　　　　　  C．18　　　　　　 D．19

6．设ｆ(x)= x²+ax+b，且1≤f(－1)≤2，2≤f(1)≤4，则点(a，b)在aOb平面上的区域的面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．　　　　　　　  B．1　　　　　　  C．2　　　　　　  D．

7．已知向量=(2,1)， =(1,7)， =(5,1)，设X是直线OP上的一点(O为坐标原点)，那么的最小值是

A．－16 B．－8　　　　　  C．0　　　　　　  D．4

8．直线 + =1与椭圆 + =1相交于A、B两点，椭圆上的点P使△PAB的面积等于12．这样的点P共有

A．1个　　　　　　　B．2个　　　　 　 C 3个　　　　　　 D．4个

9．函数y=f(x)与y=g(x)有相同的定义域，且都不是常数函数，对定义域中任何x，有f(x)+f(－x)=0，g(x)·g(－x)=1，且当x≠0时，g(x) ≠1，则＝＋

A．是奇函数但不是偶函数　　　　　　　  B．是偶函数但不是奇函数

C．既是奇函数又是偶函数　　　　　　　  D．既不是奇函数也不是偶函数

10．当x∈［0,2］时，函数f(x)=ax²+4(a－1)x－3在x=2时取得最大值，则a的取值范围是

　　 A．[－,+∞]　　　　 B．[0，+∞]　　　C．[1, +∞]　　　　 D．[,+∞]

 

二、填空题（每小题4分，共20分）

11．设双曲线的右准线与两条渐近线交于A、B两点，右焦点为F，且FA⊥FB，则双曲线的离心率为（　）．

　

12．已知一个球的半径为1，若使其表面积增加到原来的2倍，则表面积增加后球的体积是______________．

13．函数的单调递减区间是______________．

14．已知、是实数，给出下列四个论断：（1），（2），（3），，（4）．以其中的两个论断为条件，其余两个论断作为结论，写出你认为正确的一个命题：________．

15．一天内的不同的时刻，经理把文件交由秘书打字。每次都将文件堆放在秘书的文件堆的上面，秘书有时间就将文件最上面的那份文件取来打字。若有5份文件，且经理是按1，2，3，4，5的顺序交来的，在下列的顺序①12345，②32415，③24351，④54321，⑤45231中，秘书打字的可能顺序是________（只要填上序号）．

三、解答题（本大题共6题80分。解答应写出文字说明，证明过程或演算步骤）

16．（本题共12分，第①小题4分，第②小题4分，第③小题4分）

已知f(x)=2sin(x+)cos (x+)+2cos²(x+)－

①求f(x)的最小正周期

②若0≤≤求使f(x)为偶函数的的值。

③在②条件下，求满足f(x)=1, x∈[－]的x的集合。

17．（本题12分。第①题5分，第②题7分）

如图，正四棱柱ABCD—A₁B₁C₁D₁，AA₁=AB，点E、M分别为A₁B，C₁C的中点，过A₁、B、M三点的平面A₁BMN交C₁D₁于点N。

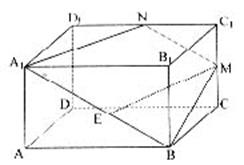①求证：EM∥A₁B₁C₁D₁

②求二面角B—A₁N—B₁正切值。

18、（本题共14分）

　设数列{a_n}和{b_n}满足a₁=b₁=6，a₂=b₂=4，a₃=b₃=3，且数列{a_n+1－a_n}（n∈N*）是等差数列，数列{b_n－2} (n∈N*)是等比数列。

（1）设C_n=a_n+1－a_n，求数列{C_n}的通项公式

（2）求数列{a_n}和{b_n}的通项公式。

（3） 是否存在k∈N*，使得a_k－b_k∈（0，）？若存在，求出k；若不存在，请说明理由。

19．（本题14分）某学校为了解决教职工的住房问题，计划征用一块土地盖一幢总面积为A（m²）的宿舍楼。已知土地的征用费为2388元/m²，且每层的建筑面积相同，土地的征用面积为第一层的2.5倍。经工程技术人员核算，第一、二层的建筑费用相同，都为445元/m²，以后每增高一层，其建筑费用就增加30元/m²。试设计这幢宿舍楼的楼高层数，使总费用最少，并求出其最少费用。（总费用为建筑费用与征地费用之和。）

20．（本题14分。第（1）题7分，第（2）题7分）

　已知椭圆C₁：=1（a>b>0）的一条准线方程为。其左、右顶点分别是A、B；双曲线C₂：=1的一条渐近线方程为3x－5y=0。

（1）求椭圆C₁的方程及双曲线C₂的离心率。

（2）在第一象限内，取双曲线C₂上的一点P，连结AP交椭圆C₁于点M，连结PB并延长交椭圆C₁于点N，若AM=MP，求证：MN·AB=0

21．（本题共14分，第（1）题3分，第（2）题4分，第（3）题7分）

已知函数f(x)=(a∈R且x≠a)

（1）求证：f(x)+2+f(2a－x)=0对定义域内的所有x都成立

（2）当f(x)的定义域为[a+，a+1]时，求f(x)的值域。

（3）设函数g(x)=x²+(x－a)f(x)，求g(x)的最小值。

参考答案

一、选择题：本大题共10小题，每小题5分，共50分．

1．C．　　2．A　　　3．A　 　 4．D　　　5．C　　  6． B 

7．B　　　8．B　　  9．B　　　10．D　

二、

11.　12．　　13．[-1，3]（填（-1，3）也算对）

14．①③②④由①知与同号，故②成立；再由③得故④成立

15．①②③④

三、解答题（本大题共6题80分。解答应写出文字说明，证明过程或演算步骤）

16．解：①f(x)=sin(2x+)+[2cos² (x+－1)]

=sin (2x+)+cos (2x+)=2cos (2x+－)…………………（3分）

（或f(x)=2sin(2x++)）

∴f(x)的最小正周期为…………………………………………4分

②f(－x)=cos (－2x+－)=cos[2x－(－)]=cos2xcos (－)+sin2xsin(－)

f(x)=cos(2x+(－)=cos2xcos(－)－sin2xsin(－)……………………（6分）

∵f(x)是偶函数，∴f(x)=f(－x)即sin2xsin(－)=0，∴sin(－)=0

∵0≤≤，－≤－≤，∴(－)=0，=………………………（8分）

③由f(x)=1得2cos2x=1，∴cos2x=………………………………（10分）

∵x∈[，]，∴x=±或x=±

所以x的集合是{－，，－，}…………………………（12分）

17．解：（I）证明：取A₁B₁的中点F，连EF，C₁F

==

∵E为A1B中点，∴EF∥　BB₁………………………………2分

==

又∵M为CC₁中点　　∴EF∥　C₁M

∴四边形EFC₁M为平行四边形

∴EM∥FC₁……………………4分

而EM平面A₁B₁C₁D₁，FC₁平面A₁B₁C₁D₁

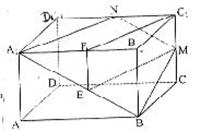∴EM∥平面A₁B₁C₁D₁……………………5分

（II）由（I）EM∥平面A₁B₁C₁D₁　EM平面A₁BMN

平面A₁BMN∩平面A₁B₁C₁D₁=A₁N　　∴A₁N∥EM∥FC₁

∴N为C₁D₁中点

过B₁作B₁H⊥A₁N于H，连BH，根据三垂线定理BH⊥A₁N

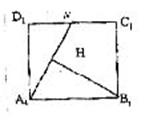∴∠BHB₁即为二面角B—A₁N—B₁的平面角…………………8分

设AA₁=a，则AB=2a，∵A₁B₁C₁D₁为正方形

∴A₁N=a，又∵△A₁B₁H∽△NA₁D₁　 ∴B₁H=

在Rt△BB₁H，tan∠BHB₁===

即二面角B—A₁N—B₁的正切值为……………………………………12分

（B）（I）建立如图所示空间直角坐标系，设AB=2a，AA₁=a（a >0），则

A₁(2a，0，a)，B（2a，2a，0），C（0，2a，0），C₁（0，2a，a）………………2分

∵E为A₁B的中点，M为CC₁的中点　∴E（2a，a，），M（0，2a，）

∴EM∥平面A₁B₁C₁D₁……………………………………5分

（II）设平面A₁BM的法向量为n=（x，y，z）

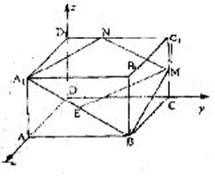
又A₁B=（0，2a，－a）　　BM=（－2a，0，）

由n⊥A₁B，n⊥BM，得

 2ay－az=0

　　　　　　　 ，∴

 －2ax+=0

∴取n=（）………………………………9分

而平面A₁B₁C₁D₁的法向量n₁=（0，0，1），设二面角为，则

又：二面角为锐二面角　　∴cos=，……………11分

从而tan=………………………………………………………………12分

18、解：（I）由已知a₂－a₁=－2，a₃－a₂=－1，则{C_n}的公差为1………………1分

∴a_n+1－a_n=（a₂－a₁）+（n－1）=n－3，即C_n=n－3……………………3分

（II）n≥2时，a_n=（a_n－a_n－1）+（a_n－1－a_n－2）+…+（a₂－a₁）+a₁

　　　 =（n－4）+（n－5）+…+（－1）+（－2）+6=

当n=1也适合上式，∴a_n=（n∈N*）………………………………5分

又b₁－2=4、b₂－2=2。而　 ∴b_n－2=（b₁－2）·

即b_n=2+

∴数列{a_n}、{b_n}的通项公式为：a_n=，b_n=2+…………7分

（III）

解法一：设f(k)=a_k－b_k=k²－K+7－8·=(k－)²+－8·……9分

当k≥4时(k－)²+为k的增函数，－8·也为k的增函数，

∴当k≥4时f(k)=a_k－b_k为k的增函数………………………………10分

而f(4)= ，∴当k≥4时a_k－b_k≥……………………………………11分

又f(1)=f(2)=f(3)=0　　 ∴不存在k，使f(k)∈（0，）……………………12分

解法二：设f(k)= a_k－b_k=k²－K+7－8·…………………………8分

f(k+1)－f(k)

=[(k+1)²－(k+1)+7－8·]－[k²－K+7－8·]

=k－3+2²－k

当k≥4时，f(k+1)－f(k)>0，f(k)为k的增函数，……………………10分

以下同解法一。

19．解：设楼高为n层，总费用为y元，则征地面积为，征地费用为元………………2分

楼层建筑费用为{445+445+（445+30）+（445+30×2）+…+[445+30×（n－2）]}·

=（15n++400）A……………………………………6分

从而y=+15Na++400A…………………………8分

y=（15n++400）A≥1000A（元）………………………………10分

当且仅当15n=，n=20（层）时，总费用y最少。

故当这幢宿舍档的楼高层数为20层时总费用最少，最少总费用为1000A元。……12分

20．解：（I）由已知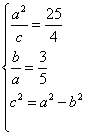　　　　  解之得：　………………………3分

∴椭圆的方程为=1，双曲线的方程

又C=　 ∴双曲线的离心率e₂=………………………6分

（Ⅱ）由（I）A（－5，0），B（5，0）。设M（x）则由得M为AP

的中点

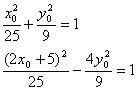∴P点坐标淡（2x）将M、P坐标代入c₁、c₂方程得　消去y₀得2x+5x-25=0解之得x₀=或x₀= -5(舍)　由此可得P（10，3）当P为

（10，3）时，PB：y=

代入　　得：2x²－15x+25=0　　 x=或x=5（舍）

∴x_N=　　  ∴x_N= x_M　　 MN⊥x轴　　 即………………………（12分）

21．（I）证明：f(x)+2+f(2a－x)=

=∴结论成立………………………3分

（Ⅱ）证明：f(x) =………………………………4分

当a+≤x≤a+1时，－a-1≤-x≤-a-,-1≤a-x≤-,-2≤

则－3≤－1+≤－2，即f(x)值域为[－3，－2]…………………7分

（Ⅲ）解：g(x)=x²+x+1－a(x≠a)=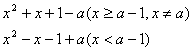……………8分

（1）　　　 当x≥a－1且x≠a时，g(x)=x²+x+1－a=(x+)²+

如果a－1=－即a≧时，则函数在[a－1,a]和（a,+）上单调调递增

g(x)_min=g(a－1)=(a－1)²

如果a－1<－即a<且a≠－时，g(x)_min=g(－)=－a

当a=－时，g(x)最小值不存在………………………………………………10分

（2）当x<a－1时g(x)=x²-x－1+a=(x－)²+a－

如果a－1>即a>时，g（x）_min=g()=a－

如果a－1≤即a≤时g(x)在（－,a－1）上是减函数，g(x)>g(a－1)=

(a－1)²……………………………………………………………………………12分

当a>时(a－1)²－(a－)=（a－）²>0,即（a－1）²>(a—)

当a<且a≠－时，(a－1)²－(－a)=(a－)²>0,即(a－1)²>( －a)……………………………………………………………………………………13分

综合得：

a<且≠－是g(x)最小值是－a

当≤a≤时　g(x)最小值是(a－1)²

当a>时　 g(x)最小值为a－

当a=－时　 g(x)最小值不存在…………………………………………………14分