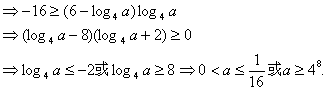高考数学模拟考试题（理科卷4）
时量120分钟 总分150分
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
１．设曲线
在点M处切线斜率为3，则点M的坐标为
A．(0,-2) B．(1,0) C．(0,0) D．(1,1)
２．如果命题“ (p或q)”为假命题，则
A．p、q均为真命题 B．p、q均为假命题
C．p、q中至少有一个为真命题 D．p、q中至多有一个为真命题
３．已知集合M={
，
}，N={
}，P={
}，则下列关系式中成立的是
|
|
|
|
NM B．P＝NM C．PN＝M D．P＝N＝M
４．若函数y=f(x-1)是偶函数，则y=f(x)的图象关于
A．直线x+1=0对称 B．直线x-1=0对称
C．直线x-
=0对称
D．y轴对称
５．{
}为公比q的等比数列，则
>0，q>1是{}为递增数列的
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．以上均不对
６．从正方体的八个顶点中任取4个，其中4点恰能构成三棱锥的概率为
A．
B．
C．
D．
７．将函数y=3sin(2x+
)的图象按向量
平移后所得图象的解析式是
A．y=3sin(2x+
)-1
B．y=3sin(2x+)+1
C．y=3sin2x+1
D．y=3sin(2x+
)-1
８．已知
、
是直线，
是平面，给出以下四命题：
①
；②
；③
；④
其中正确的命题是
A．① ② B．① ② ③ C．① ② ④ D．② ③ ④
９．二项式
展开后所得的x的多项式中，系数为有理数的项共有
A．4项 B．5项 C．6项 D．7项
10. 显示屏有一排7个小孔，每个小孔可显示0或1，若每次显示其中3个孔，但相邻的两孔不能同时显示，则该显示屏能显示信号的种数共有
A．10 B．48 C．60 D．80
二.填空题: 本大题共5小题,每小题4分,共20分,把答案填在题中横线上.
11．对某种产品的6件不同正品和4件不同次品一一进行测试，到区分出所有次品为止。若所有次品恰好在第五次测试被全部发现，则这样的测试方法有
12.在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1=
.
13.一个圆柱形容器的内半径为5cm,两个直径为5的玻璃小球被浸没于容器的水中,当取出这两个小球后, 容器的水面下降了x cm, 则x= .
14.某校有学生宿舍若干间,现安排高三女生居住,若每间住5人,余60人. 若每间住10人,则有一间宿舍不空也不满,则高三女生有 人,宿舍有 间.
15.已知双曲线
的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
三.解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16.( 本小题满分12分)
已知复数z=sinB+(1-cosB)i ,argz=
A, B, C是⊿ABC的内角。
（１）求Ｂ； （２）求sinA+sinC的取值范围。
.
A
17. .( 本小题满分12分)
如图，正三角形ABC与直角三角形BCD成直二面角，
且∠BCD=90
,∠CBD=30.
(１) 求证：AB⊥CD;
B
C
（２）求二面角D-AB-C的正切值。 D
（3） 求异面直线AC和BD所成的角。
18 .( 本小题满分14分)
经过抛物线y
的焦点F的直线L与该抛物线交于A,B两点.
（1） 若线段AB的斜率为k，试求中点M的轨迹方程；
（2）
若直线的斜率k＞2，且点M到直线3 x+4y+m=0的距离为
，试确定m的取值范围。
19. .( 本小题满分14分)
设数列
前项和为
,且(3
,其中m为常数,m
(1) 求证:是等比数列;
(2) 若数列的公比q=f(m),数列
满足
求证:
为等差数列,求
.
20. 随着我国加入WTO，某企业决定从甲、乙两种产品中选择一种进行投资生产，打入国际市场。已知投资生产这两种产品的有关数据如下表（单位：万美元）
|
类 别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多生产的件数 |
| 甲产品 | 30 | a | 10 | 200 |
| 乙产品 | 50 | 8 | 18 | 120 |
项 目 其中年固定成本与生产的件数无关，a为常数，且4≤a≤8。令外，年销售x件乙产品时需上交0.05x
万美元的特别关税。
（１）
写出该厂分别投资生产甲、乙两种产品的年利润y
,y
与生产相应产品的件数x (x
之间的函数关系式；
（２） 分别求出投资生产这两种产品的最大年利润；
（３） 如何决定投资可获最大年利润。
.
21. ( 本小题满分14分)
已知 函数f(x)=
的图像关于原点对称，其中m,n为实常数。
（１） 求m , n的值；
（２） 试用单调性的定义证明：f (x) 在区间[-2, 2] 上是单调函数；
（３） [理科做] 当-2≤x≤2 时，不等式
恒成立，求实数a的取值范围。
参 考 答 案
一、选择题
Ｂ、Ｃ、Ａ、Ａ、Ａ、 Ｃ、Ａ、Ａ、Ｄ、 Ｄ、
二.
11.576种 ; 12. 4,12 13.
.
14.125,13.
15.1<e
.
三.
16.
∵argz=
,∴
∴tan
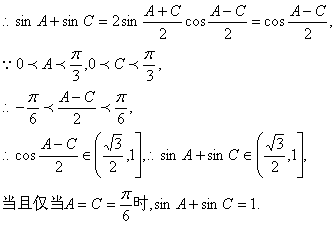
(17) (
1)∵平面ABC⊥平面BCD, ∠BCD=90,∴CD⊥平面ABC.
∵AB
平面ABC, ∴CD⊥AB.
(2)过点C作CM⊥平面ABC于M,连DM,由(1)知CD⊥平面ABC,
∴DM⊥AB.∴
∠CMD是二面角
D-AB-C的平面角.
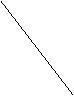设,CD=1,由∠BCD=90,∠CBD=30,BC=
A
∵⊿ABC是正三角形, ∴CM=
M N
∴tan∠CMD=
B
O
C
故二面角D-AB-C的正切值为 
.
D
21. 取三边AB,AD,BC的中点M .N . O,连AO,NO,MN,OD.则OM平行且等于
AC,MN平行且等于BD.
∴直线OM和MN所成的锐角或直角就是直线AC和BD所成的角.
∵⊿ABC是正三角形,且平面ABC⊥平面BCD,
∴AO⊥平面BCD,∴⊿AOD是直角三角形,
ON=
又∵CD⊥平面ABC,
∴AD=
在⊿OMN中,OM=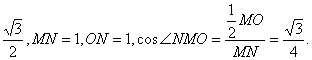
∴直线AC和BD所成角为arccos
.
18.(1)设A(
直线AB的方程为y=k(x-1) (k≠0),代入
,得
kx-(2k+4)x+k=0
设M(x ,y).则
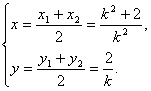
∴点M的坐标为(
消去k可得M的轨迹方程为
(2)由 d=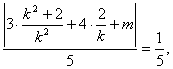
得 
即 0＜
＜,得
0＜
,
即 
或 
故的取值范围为 (-
（19）（1）由
∴是等比数列。
（2）
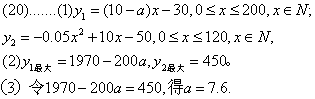
当4
时，投资甲产品；当7.6<a
时，投资乙产品；当a=7.6时，投资甲、乙两产品均可。
21. (1)由于f(x)图象关于原点对称，则f(x)是奇函数,
f(-x)=-f(x)
∴f(x)在[-2,2]上是减函数。
（3）由（2）知f(x)在[-2,2]上是减函数，则-2
时,
故-2
不等式f(x)
恒成立
