高考数学摸底试题试题
注意:答案一律写在答题纸上
一、填空(10×3)
1．若sina=
,a∈(0, π/2),则tga= .
2．数列
满足
，a1=1则
.
3．双曲线的渐近线为
,它的一个顶点为（1，0），则双曲线方程为
。
4．数列是公差不为0的等差数列，且
为等比数列
的连续三项，若b1=1，则b2005= 。
5．在集合
中任取一个元素，所取元素恰好满足方程
的概率是 。
6．若一条曲线既是轴对称图形又是中心对称图形，则称此曲线为双重对称曲线，下列四条曲线①
②
③
④y=sinx中，双重对称曲线的序号是
。
7． F1、F2是椭圆
的左、右两焦点，P为椭圆的一个顶点，若△PF1F2是等边三角形，则a2=
。
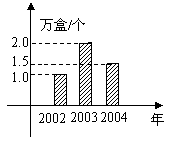8．一个高中研究性学习小组对本地区2002年至2004年快餐公司发展情况进行了调查，根据图中的信息可以得出这三年中该地区每年平均销售盒饭 万盒。
 |
|
|
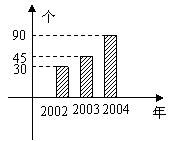9．等比数列的首项
，公比
，记
,则pn达到最大值时，n的值为
。
10．若AB是过二次曲线中心的任一条弦，M是二次曲线上异于A、B的任一点，且AM、BM均与坐标轴不平行，则对于椭圆
有
。类似地，对于双曲线
有
=
。
二、选择(6×3)
11．已知函数
是以
为周期的奇函数, 则f(x)可以是（ ）
（A）sin2x （B）cos2x （C）sinx （D）cosx
12．F1（-1，0）、F2（1，0）是椭圆的两焦点，过F1的直线l交椭圆于M、N，若
△MF2N的周长为8，则椭圆方程为（ ）
（A）
（B）
（C）
（D）
13．定义在R上的函数f(x)对任意两个不相等的实数a、b,总有
成立，则f(x)必定是（ ）
（A）奇函数 （B）偶函数 （C）增函数 （D）减函数
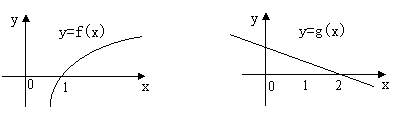14． y=f(x),y=g(x)的图象如下,f(1)=g(2)=0,则不等式
的解集是（ ）
（A）
（B）
（C）
（D）
15． 命题A：若x>0,则
<1, 命题B：函数
在
上为减函数。
若A与B中至少有一个是真命题，则实数a的取值范围是（ ）
（A）
（B）
（C）
（D）
16．等差数列的前n项和为Sn，已知
,则（ ）
（A）n=5时，Sn有最大值 （B）n=6时，Sn有最大值
（C）n=5时，Sn有最小值 （D）n=6时，Sn有最小值
三、解答(5+6+8+10+11+12)
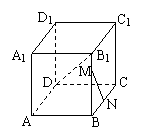17．长方体ABCD-A1B1C1D1中，M，N分别是BB1和BC的中点，AB=4，AD=2，B1D与平面ABCD所成角的大小为60。，求异面直线B1D与MN所成角的大小。
18．曾记否？复数
，
。
已知
,
，求
的取值范围。
19．对于数列
，有
，且
,
求: （1）p的值
（2）的通项公式
20．曲线C上的动点P到定点Q（1，0）与它到直线x+1=0的距离相等。求：
（1）曲线C的方程；
（2）过点Q的直线
与曲线C交于A、B两点，求证：
为定值。
（温馨提示：
，则
）
21．已知
（1）
, 求
的最小值
（2）P、Q关于点（1，2）对称，若点P在曲线C上移动时，点Q的轨迹是函数的图象，求曲线C的轨迹方程。
（3）在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式。如从可抽象出
的性质，试分别写出一个具体的函数，抽象出下列相应的性质
由
可抽象出
由
可抽象出
22．上海电信宽频私人用户月收费标准如下表
| 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 130元 | 无 |
| 乙 | 有限包月制（限60小时） | 80元 | 3元/小时 |
假定每月初可以和电信部门约定上网方案
1）某用户每月上网时间为70小时，应选择哪种方案
2）写出方案乙中每月总费用y(元)关于时间t（小时）的函数关系式
3）费先生一年内每月上网时间t(n)（小时）与月份n的函数为
，问费先生全年的上网费用最少为多少元
川沙中学2006届高三数学摸底考试答题纸
一填空
1.___ 
_____, 2._____2_____,
3.___ 
______, 4._____22004_____,
5.____ 
_____, 6.
_____(1)(2)(4)____, 7.____12_____, 8._____85_____,
9.___10______,
10.____ 
_____,
二选择
11.___D____, 12____A___, 13.___C____, 14.___B____, 15.__B_ , 16.___C____,
三解答
17．
BB1
平面ABCD，
BB1B=60
BB1=BDtg60=2
………………2’
又MN//B1C,DB1C是异面直线B1D与MN做成的角……………………3’
tgDB1C=
DB1C=arctg
…………………………………………4’
异面直线B1D与MN所成角的地小为arctg………………………………5’
18．解：，
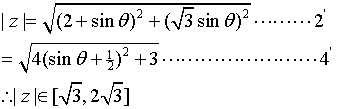
（区间端点错一个扣1分）………………………………６’
19. (1)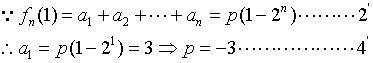 
(2) 
时
……7’
又 
（写成
不扣分）…………8’
20. (1) 
4’
(2)设
代入得
……6’
设A(x1,y1)B(x2,y2),则x1+x2=2+
,x1x2=1
=-3……9’
当
斜率不存在时，也成立
…………10’
21. (1) 
…………3’
等号当x=2时成立， 
…………………………4’
(2)设P(x,y)则Q(2-x,4-y)………………………………………………5’
由4－y=lg(2－x)可得：y=4－lg(2－x)………………………………８’
(3) h(x)=_______y=2x等_______, ９’ φ(x)=____y=lgx等__11’
22. (1)乙方按月费用为：80+10
３＝110元…………………………２’
110<130应选择乙方案；…………………………………………３’
(2) 
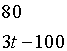
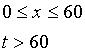…………7’（写成０<x<60不扣分）
(3)由3t－100<130 得：
当
时，选择乙方案，当
时，选甲方案。…………9’
即：前11个月选择乙方案，最后一个月选择甲方案。…………………………10’
总费用＝［80+3(f(1)－60)］+[80+3(f(2)－60)]+…+[80+3(f(n)－60)＋120=1280元…12’