1、已知函数y=![]() 满足
满足![]() ,且方程
,且方程![]() =0有n个实根x1,x2,…xn,则x1+x2+…+xn= 3n 。
=0有n个实根x1,x2,…xn,则x1+x2+…+xn= 3n 。
解:由![]() 可得y=
可得y=![]() 的图像图像关于x=3对称。
的图像图像关于x=3对称。
当n为偶数时,方程![]() =0有n个实根x1,x2,…xn两两成对出现,且成对两根之和为6,
=0有n个实根x1,x2,…xn两两成对出现,且成对两根之和为6,
所以x1+x2+…+xn=6×![]() =3n
=3n
当n为奇数时,方程![]() =0有n个实根中必有一根为3,其余n-1个根两两成对出现,且成对两根之和为6,所以x1+x2+…+xn=3+3(n-1)=3n
=0有n个实根中必有一根为3,其余n-1个根两两成对出现,且成对两根之和为6,所以x1+x2+…+xn=3+3(n-1)=3n
故x1+x2+…+xn=3n。
2、对一个各边不等的凸五边形的各边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.则共有 30 种不同的染色方法。
解:记凸五边形的各边分别为①、②、③、④、⑤
第一步:将五边分成三组且相邻边不在同一组,则有
①、②④、③⑤ ②、①④、③⑤
③、①④、②⑤ ④、①③、②⑤
⑤、①③、②④
故共有五组
第二步:将三种颜色对应三组进行全排列A![]() =6
=6
由分步计数原理得共有5×6=30种。
3、如图1,设P、Q为△ABC内的两点,且![]() ,
,
![]() =
=![]()
![]() +
+![]()
![]() 则△ABP的面积与△ABQ的面积之比为 ( B )
则△ABP的面积与△ABQ的面积之比为 ( B )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
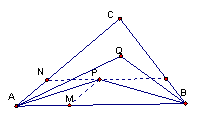
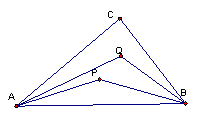
图1 图2
解:如图2设![]() ,
,![]() 则
则![]() 由平行四边形法则知NP∥AB,所以
由平行四边形法则知NP∥AB,所以 =
=![]() ,同理可得
,同理可得![]() 。
。
故![]() 即选B.
即选B.
4、设x>1,S=min{logx2,log2(4x3)}则S的最大值为 3 。
解:由题设知S![]() logx2,S
logx2,S![]() log2(4x3),且S>0则
log2(4x3),且S>0则
S![]() log2(4x3)=2+3log2x=2+
log2(4x3)=2+3log2x=2+![]()
![]() 2+
2+![]() ,
,
于是S2-2S-3![]() 0得-1
0得-1![]() S
S![]() 3当x=
3当x=![]() 时取等号。
时取等号。
5、在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),C点在AB上且OC是∠AOB的角平分线,则![]() = (-
= (-![]() ,
,![]() ) 。
) 。
解:由题设知![]() =(0,1),
=(0,1),![]() =(-3,4)
=(-3,4)
![]() OC是∠AOB的角平分线
OC是∠AOB的角平分线
![]() 可设
可设![]() =
=![]() (
(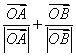 )=
)=![]()
![]() +
+![]()
![]()
![]()
又C点在AB上
所以![]() +
+![]()
![]() =1解得
=1解得![]() =
=![]()
故![]() =
=![]()
![]() +
+![]()
![]() =(-
=(-![]() ,
,![]() )
)
6、在十进制中,若一个至少有两位数字的正整数除了最左边的数字外,其余各个数字都小于其左边的数字时,则称它为递降正整数.所有这样的递降正整数的个数为(D )
(A)1001 (B)1010 (C)1011 (D)1013
解:当正整数为两位数时,有![]() 个
个
当正整数为三位数时,有![]() 个
个
………
当正整数为十位数时,有![]() 个
个
由分类计数原理得共有正整数![]() +
+![]() +…+
+…+![]() =210-
=210-![]() -
-![]() =1013
=1013
故选D。
7、已知![]() ,设
,设![]() ,记
,记![]()
(1)求证:tan![]() =2tan
=2tan![]()
(2)求![]() 的表达式;
的表达式;
(3)定义正数数列{an};a1=2,![]() =2
=2![]()
![]()
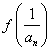 (n
(n![]() )。
)。
试求数列![]() 的通项公式。
的通项公式。
解:(1)由![]() ,得sin
,得sin![]() =3sin
=3sin![]() ,即
,即
sin![]() cos
cos![]() =2cos
=2cos![]() sin
sin![]()
故tan![]() =2tan
=2tan![]()
(2)由tan![]() =2tan
=2tan![]() 得
得![]() 即
即![]() 。解得
。解得
y=![]() 故
故![]() =
=![]()
(3)因为![]() =2
=2![]()
![]()
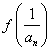 =2
=2![]()
![]()
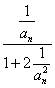 ,
,
所以![]() =
=![]()
![]() +1即
+1即![]() -2=
-2=![]() (
(![]() -2)
-2)
因此{![]() -2}是首项为2,公比为
-2}是首项为2,公比为![]() 的等比数列。
的等比数列。
所以![]() -2=2
-2=2![]() 故an=
故an=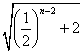 。
。
8、平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足 ![]() 、
、![]()
(1)求点C的轨迹方程;
(2)设点C的轨迹与椭圆![]() 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证:![]()
(3)在(2)的条件下,若椭圆的离心率不大于![]() ,求椭圆实轴长的取值范围.
,求椭圆实轴长的取值范围.
解:(1)设![]()
![]()
即点C的轨迹方程为x+y=1 。
(2)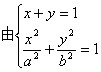 得:(a2+b2)x2-2a2x+
a2- a2b2=0
得:(a2+b2)x2-2a2x+
a2- a2b2=0
设M(x1,y1),N(x2,y2),则“
x1+ x2=![]() , x1x2=
, x1x2=![]()
因为以MN为直径的圆过原点为,
所以![]() =0,即x1x2+y1y2=0
=0,即x1x2+y1y2=0
∴x1x2+(1-x1)(1-x2)=1-(x1+
x2)+2 x1x2=1-![]() +2
+2![]() =0
=0
即a2+b2-2 a2b2=0
∴![]()
(3)![]()
![]()
∴椭圆实轴长的取值范围是(0,![]()
![]() 。
。