1. 函数 
R) 的最小值是
.
解：令 
，则 
．
当 
时， 
，得 
；
当 
时， 
，得 
又 
可取到 
, 故填 ．
2．手表的表面在一平面上。整点1，2，…，12这12个数字等间隔地分布在半径为
的圆周上。从整点i到整点（i＋1）的向量记作
，则
＝ 
。
解：连接相邻刻度的线段构成半径为的圆内接正12边形。相邻两个边向量的夹角即为正12边形外角，为30度。各边向量的长为
。 则
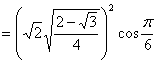
。共有12个相等项。所以求得数量积之和为 。
3．设
，则对任意实数
，
是
的（ A ）
A. 充分必要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
解：显然为奇函数，且单调递增。于是
若，则
，有
，即
，从而有.
反之，若，则
,推出 ，即 。
故选A。
4．椭圆
的中心，右焦点，右顶点，右准线与
轴的交点依次为
，则 
的最大值为（ ）.
不能确定.
答：
．
解：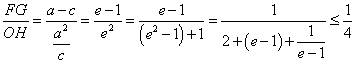 
.（
时取等号）
5．过椭圆
的一个焦点 F作弦AB，则
=
。
解：不妨设焦点F为右焦点，则F（4，0）。当AB
x轴时，A（4，
），B（4，-）
所以
=，故=
6．已知常数
，经过定点A（0，-a）以（l，a）为方向向量的直线与经过定点B（0，a）以（1，－2la）为方向向量的直线相交于点P，其中
试问：是否存在两个定点E、F，使得PE+PF为定值.若存在，求出E、F的坐标；若不存在，说明理由.
解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到两定点距离的和为定值．
因此，直线AP和BP的方程为
l（y+a）=ax 和 y－a＝－2lax．
消去参数l，得点P（x，y）的坐标满足方程y2-a2=－2a2x2，
整理得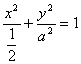 
． ①
因为a>0，所以得：
（ⅰ）当
时，方程①是圆方程，故不存在合乎题意的定点E和F；
（ⅱ）当
时，方程①表示椭圆，焦点
和
为合乎题意的两个定点：
（ⅲ）当
时，方程①也表示椭圆，焦点
和
为合乎题意的两个定点．
7.已知A（2cos
,
），B（2cos
,
），C（-1,0）是平面上三个不同的点，若存在
，使得
，试求的取值范围。
解：由已知，可得
（2cos+1, ）=（-1-2cos,-）,
,
,
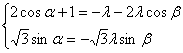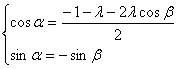由
=1，得
，
即
，
若=-1，则
，得
，这与A，B两点不重合矛盾，
因此，
-1，于是
，可知0，
，得
，
解得
3。