高考数学最后冲刺训练2

高考数学最后冲刺训练

　　　　　　　　  撰稿：王思俭（苏州中学  特级教师 教研组长）

联想与激活（3）

1．已知集合A｛0，1，2，3｝，且A中至少有一个奇数，这样的A有（　　 ）

　A．11个　　　　 B．12个　　　　 C．9个　　　　D．以上都不对

联想：（1）集合A=｛｝，则集合A的子集共有　　　　个。

（2）用数字1，2，3组成没有重复数字的自然数，以这些自然数的若干个为元素的集合（非空）的个数为　　　 个。

（3）已知集合M=｛－1，1，2，4｝，N=｛0，1，2｝，给出下列四个对应法则：①y=x²,②y=x+1,③y=2^x,④y=log₂，其中能构成从M到N的函数的是（　　 ）

　A．①　　　　　　B．②　　　　　　C．③　　　　　　D．④

2．已知y=f (x+1)是奇函数，且f (x)的图象关于直线x=2对称，当0≤x≤1时，f (x)=2^x，则f (log₂24)的值为（　　 ）

　A．　　　　　  B．　　　　　　 C．　　　　　 D．

联想：（1）函数y=x³的图象在点（1，1）处的切线方程为（　　 ）

　A．y=x　　　　　  B．y=2x－1　　　　C．y=3x－2　　　D．y=4x－3

（2）函数y=lg(1－)的图象（　　 ）

　A．关于原点对称　　B．关于x轴对称　 C．关于y轴对称　　D．关于直线x=1对称

（3）函数f (x)=的奇偶性是（　　 ）

　A．奇函数　　　　　 B．偶函数　　　　  C．奇偶兼备　　　　D．非奇非偶函数

（4）已知函数f (x)满足f (x²－3)=lg，则y=f (x)在定义域内（　　 ）

　A．是奇函数且是增函数　　　　　　　 B．是奇函数且是减函数

C．是偶函数　　　　　　　　　　　　 D．是增函数，但既不是奇函数也不是偶函数

3．设函数y=(cosx－m)²－1，当cosx=－1时，取最大值，当cosx=m时，取最小值，则实数m必是（　　 ）

　A．0≤m≤1　　　　　 B．－1≤m≤0　　　　 C．m≤－1　　　　　 D．m≥1

联想：（1）函数y=asinx+bcosx(x∈R)的最大值为，则a+b的最小值为（　　 ）

　A．2　　　　　　  B．－2　　　　　 C．　　　　　　　 D．－

（2）若函数y=2sinx+cosx+4的最小值为1，则a=　　　 。

（3）若函数y=cos2x+asinx+1的最大值为2，则a=　　　 。

（4）函数y=sinx+cosx+sinxcosx的最大值为　　　　，最小值为　　　 。

4．已知a、b是直线，α、β、 是平面。给出下列命题：①a∥α，a∥β，α∩β=b，则a∥b；②α⊥，β⊥，α∥β；③a⊥α，b⊥β，a⊥b，则α⊥β；④α∥β，β∥，a⊥α，则a⊥。其中正确命题的序号是（　　 ）

　A．①②④　　　　　B．①③④　　　　　　　C．②④　　　　　D．②③

联想：（1）已知直线⊥平面α，直线mβ，有下面四个命题：

①α∥β⊥m；②α⊥β∥m；③∥mα⊥β；④∥mα∥β。其中正确的两个命题是（　　 ）

　A．①与②　　　　B．③与④　　　　C．②与④　　　　D．①与③

（2）已知集合A、B、C，A=｛直线｝，B=｛平面｝，C=A∪B若a∈A，b∈B，c∈C，在下面命题中

a⊥b　　　　　　　　  a⊥b　　　　　　　 a∥b　　　　　　　  a∥b

①　　　　a∥c　　　②　　　 a⊥c　　③　　　a∥c　 　④　　　 a⊥c　

c⊥b　　　　　　　　  c∥b　　　　　　　 b∥c　　　　　　　  c⊥b

正确命题的序号是　　　　　　　 。（注：把你认为正确的序号都填上）

（3）若a、b是两条异面直线，则存在惟一的平面β，满足（　　 ）

　A．a∥β且b∥β　　 B．aβ且b∥β　　 C．a⊥β且b⊥β　　　D．aβ且b⊥β

5．若以连续掷两次骰子分别得到的点数m、n分为点P的坐标，则点P落在圆x²+y²=16内的概率为（　　 ）

　A．　　　 B．　　  C．　　  D．

联想：（1）有红、黄、蓝三种颜色的旗帜各3面，在每种颜色的3面旗帜上分别标上号码1、2和3。现在取出3面，它们的颜色与号码均不相同的概率是　　　 。

（2）从集合｛0，1，2，3，5，7，11｝中任取3个元素分别作为方程Ax+By+C=0中的A、B、C所得恰好总经过坐标原点的直线的概率是　　　 。

（3）袋内装有大小相同的4个白球和3个黑球，从中任意摸出3个球，其中只有一个黑球的概率是

　　　　 。

（4）在大小相同的6个球中，2个是红球，4个是白球，若从中任意选取3个，则所选取的3个球中至少有一个红球的概率是　　　 。

6．在等差数列｛a_n｝中，a₁₀＜0 ，a₁₁ ＞0 ，且a₁₁＞，数列｛a_n｝的前n项和为S_n,则使S_n＜0的n的最大值是（　　 ）

　A．19　　　　  B．20　　　　 C．21　　　　  D．无穷大

联想：（1）在A·P｛a_n｝中，若a₄+a₆+a₈+a₁₀+a₁₂=120, 则2a₁₀－a₁₂的值为（　　　　）

A．20　　　　  B．22　　　　　  C．24　　　　　  D．28

（2）若正数a、b、c依次构成公比大于1的等比数列，当x＞1时，log_ax, log_bx,log_cx依次成（　　　　）

A．等差数列　　　　 B．等比数列　　　　C．各项倒数成A·P　　 D．各项倒数成G·P

（3）已知A·P｛a_n｝,｛b_n｝前n项和分别是S_n、T_n，若，则等于（　　　）

A．　　　　  B．　　　　 C．　　　　  D．

7．设函数f(x)=,利用课本中推导等差数列前n项和的公式的方法，可求得

f(－5)+f(－4)+…+f(0)+…+f(5)+f(6)的值为_______________________.

联想：（1）已知函数f(x)=,那么+(的值为___________________________。

　（2）已知函数f(x)满足：f(p+ q)=f(p)·f( q ),f(1)=3,则

+_____________________

（3）对于定义在实数集R上的函数f(x)，如果存在实数x₀, 使f(x₀)=x₀，那么x₀叫做函数f(x)的一个不动点。已知，函数f(x)=x²+2ax+1不存在不动点，那么实数a的取值范围是(　　)

A.(－)　　　　　　 B.()　　　　　  C.(－1,1)　　　 D.(－)v(1+)

8.已知a+b＞0，b=4a，（a+b）ⁿ展开式按a的降幂排列，其中第n项与第n－1项相等，那么正整数n等于（　　　）

A．4　　　　 B．9　　　　  C．10　　　　  D．11

联想：（1）在（x²+x－2）⁵的展开式中，x的系数是________________.

(2)已知（x+1）⁶(ax－1)²展开式中含x³项的系数为20，则实数a的值为______________.

(3) 若（1+2x）¹⁰⁰=a₀+a₁(x－1)+a₂(x－1)²+…＋a₁₀₀(x－1)¹⁰⁰,则a₁+a₃+a₅+…＋a₉₉=______________.

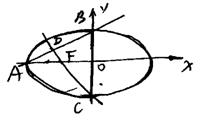9. 如图，椭圆(a＞b＞o)的离心率e=左焦点为F，A，B，C为其三个顶点，直线CF与AB交于D，则tan∠BDC的值等于（　　　　）

A．　　　　　　　 B．　　　　

C．　　　　 　　　D．

联想：（1）设双曲线的一条准线与两条渐近线交于A、B两点，相应的焦点为F，若以AB为直径的圆恰好过F点，则离心率为（　　　　  ）

A．　　　　　 B．　　　　 C．2　　　　  D．

（2）双曲线（a＞0，b＞0）的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离，则双曲线的两条渐近线的夹角为（　　  ）

A．30°　　　　B．60°　　　　C．45°　　　　  D．90°

10．设双曲线的左、右焦点为F₁、F₂，左右两顶点为M、N，若△PF₁F₂的一个顶点P在双曲线上，则△PF₁F₂的内切圆与边F₁F₂的切点的位置是（　　　 ）

A．在线段MN的内部　　　　  B．在线段F₁M内部或F₂N的内部

C．点N或M　　　　　　　　　D．以上三种情况都有可能

联想：（1）设F₁，F₂是椭圆的两上焦点，P为椭圆上一点，且∠F₁PF₂=60°，则离心率e的范围是__________________。

（2）若F₂是椭圆的右焦点，点A坐标为（1，1），则在椭圆上使2的值最小的点M的坐标是（　　　 ）

A．（）　　　　B．　　　　　C．（2，0）　　　 D．（1，）

11．这是一个计算机程序的操作说明：

①　　 初始值x=1,y=1,=0, n=0;

②　　 n=n+1.（将当前n+1的值赋予新的n）;

③　　 x=x+2(将当前x+2的值赋予新的x);

④　　 y=2y(将当前2y的值赋予新的y);

⑤　　 z=z +xy(将当前z+xy的值赋予新的z);

⑥　　 如果z＞7000,则执行语句⑦，否则回语句②继续进行；

⑦　　 打印n,z；

⑧　　 程序终止。由语句⑦打印出的数值为____________,___________.(要写出计算过程)

联想：已知数列｛a_n｝中，a₁=且对任意自然数n都有a_n+1=,数列｛b_n｝对任意自然数n都有b_n = a_n+1－a_n

(I) 求证数列｛b_n｝是等比数列；　　　 （II）求数列｛a_n｝的通项公式；

（III）设数列｛a_n｝前n项的和为Sn，求Sn的值。

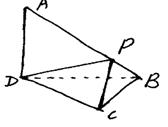
12．如图所示，△ADB和△CBD都是等腰直角三角形。

且它们所在的平面互相垂直，∠ADB=∠CBD=90°，AD=a.

（I）求异面直线AD，BC所成的角； （II）设P是线段

AB上的动点，问P、B两点间的距离多少时， △PCD与

△BCD所在平面成45°角？

（III）证明：A、B、C、D四点所在球面的面积为S，求S的值。

联想与激活（4）

1．设集合A=｛ ≤4，x｝，B=｛ ≤a，x｝，若AB，则实数a的取值范围为 （　 ）

　A．0≤a≤1　　　　  B．a≤1　　　 C．a＜1　　　　D．0＜a＜1

联想：（1）AB是成立的　　　　　  　　　　　条件

　　（2）已知集合A=｛x²－a<0｝，B=｛ x < 2｝，若AB=A，则实数a的取值范围是　　　　　　　　 

　　（3）函数f ( x )是定义在R上的减函数，图象经过点A（0，4）和点B（3，－2），且不等式＜3的解集为（－1，2），则实数a的值为（　 ）

　　　A．1　　　　　  B．－1　　　　  C．2　　　　  D．－2

　　 （4）有以下四个命题：CuAB=U（U为全集）；AB=A；AB=B；CuAB=，这中间与命题：AB等价的有　（　　）

　　　A．1个　　　　  B．2个　　　　 C．3个　　　　  D．4个

2．函数f ( x )= cos ( 3x +θ)的图象关于原点对称的充要条件是 （　　）

　A．　　  B．　　　 C．θ=kπ　　　　D．

联想：（1）已知函数f ( x )=，如果g ( x )的图象与函数y=f^－1(x+1)的图象关于x－y=0对称，那么g（2）的值为（　　）

　　　 A．－1　　　　　  B．－2　　　　　　 C．－0.8　　　　 D．－0.2

　　 （2）下列四个函数中，同时具有性质：①最小正周期为π；②图象关于直线对称的函数是（　　）

　　　A．　　　　　　　  B．

C．　　　　　　　 D．

（3）函数y=sinx－cosx与函数y=sinx＋cosx图象关于（　 ）

A．x轴对称　　　B．y轴对称　　　 C．直线对称　　D．直线对称

（4）函数y=sin2x + cos2x的图象关于直线对称，则a=（　　）

A．　　　　　  B．　　　　　  C．1　　　　　 D．－1

（5）已知x₁是方程x＋lgx=3的根，x₂是x＋10^x=3的解，那么x₁＋x₂等于（　　）

A．6　　　　　 B．3　　　　C．2　　　　　 D．1

3．将圆( x－3 )² ＋( y + 2)²=1按向量平移后，与直线y = x + 1相切，则n=（ 　）

　A．5　　　 B．或　　　　C．6　　　　D．

联想：（1）若函数y =的图象按向量（5, －5）平移后得到的函数图象与原函数的反函数的图象重合，则实数m的值为（　　）

A．2　　　　　  B．6　　　　 C．－6　　　　　　D．不存在

 （2）将函数y = cosx的图象按向量，0）平移后，得到曲线C，又设曲线C与C′关于原点对称，则C′对应的函数解析式为　　　　　　

 （3）如果函数y=ax＋b的反函数是它本身，那么点（a , b）的轨迹是（　 ）

A．定点（1 , 0）　　　　　  B．定点（－1 , 0）

C．直线a=－1　　　　　　  D．直线a=－1和定点（1 , 0）

4．设二次函数f ( x )对x恒有f (1－x) = f ( 1＋x )，且其图象开口向上，若，则p、q、r大小关系为（　 ）

　A．p > q > r　　　　B．q > p > r　　　 C．q > r≥p　　　　 D．q > p≥r

联想：（1）若x < y < 0，A=，B=，C=，D=，它们的关系是（　 ）

A．B<D<C<A　　　 B．A<D<C<B　　　 C．A<C<D<B　　　D．D<B<C<A

（2）α、β是锐角三角形的两个内角，x=sin(α+β)，y=cosα+cosβ，z=sinα+sinβ，则x、y、z的大小关系是（　　）

A．x<y<z　　　　　 B．z<y<x　　　　　 C．x<z<y　　　　  D．z<x<y

（3）△ABC中，三边a、b、c对角为A、B、C，且a>b>c，设p=sinAcosC，q=sinBcosB，r=sinCcosA，则p、q、r的大小为（　　）

A．p>q>r　　　　　  B．p>r>q　　　　　 C．r>p>q　　　　  D．r>q>p

（4）已知函数f ( x )=log₂( x +1 )且a>b>c>0，则的大小为（　 ）

A．　　　　　　　 B．

C．　　　　　　　 D．

5．将正方体的纸盒展开（如图）直线AB、CD在原正

方体中的位置关系是（　 ）

　A．平行　　　 　　　　　 B．垂直　　　

C．相交且成60⁰角　　　　D．异面且成60⁰角

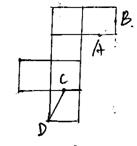
联想：（1）右图是一个正方体的表面展开图，A、B、C

均为棱的中点，D是顶点，则在正方体中，异面直线AB

和CD的夹角的余弦值为（　　）

A．　　　　 　　　　 B．　　　

C．　　　　　　　　 D．

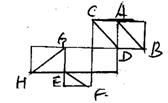
（2）右图表示一个正方体的展开图，图中AB、CD、

EF、GH这四条直线在原正方体中相互异面的有（　 ）

A．2对　　　　　　　　　　　　B．3对　　　　

 C．4对　　　　 　　　　　　　　D．5对

6．函数y=是奇函数，则θ等于（以下k）　（　 ）

　A．　　　　 B．　　　　　 C．　　　　　  D．

联想：（1）函数f ( x )=sin(wx+θ)cos (wx+θ) （w>0），以2为最小正周期，且能在x=2时取得最大值，则θ的一个值是（　 ）

　　 A．　　　　　 B．　　　　　 C．　　　　  D．

　　（2）为了使函数y=sinwx (w>0 )在区间[0，1]上至少出现50次最大值，则w的最小值是（　 ）

　　  A．98π　　　　  B．　　　　　 C．　　　　  D．100π

　　 （3）设函数f ( x ) = sin ( wx+θ) ( w > 0 , )，给出以下四个论断：

①它的图象关于直线x=对称；②它的图象关于点（ , 0）对称；

③它的周期为π；　　　　  ④在区间上是增函数；

以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个正确命题：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

7．已知展开式的第三项为20，则y关于x的函数图象的大致形状为　　　　 。

联想：（1）设f ( x )= ( x－1 )⁵ + 5 ( x －1 )⁴ + 10 ( x－1)³ + 10( x－1 )² + 5x－4的图象关于直线y=x对称图象所对应的函数为g ( x ) ，则g ( x )的解析式为（　 ）

　　　A．x⁵　　　　 B．x　　　　C．x+1　　　 D．(x－2)

　　 （2）已知，则的值为（k是小于n的最大奇数）

　　　A．64　　　　　 B．32　　　　  C．63　　　　  D．31

　　 （3）( x² + x－1)⁹ ( 2x +1 )⁴的展开式中，所有奇数次项的系数和为　　　　　  .

8．某厂生产电子元件，其产品的次品率为5%，现从一批产品中任意地连续取2件，其中次品数η的概率分布是

η	0	1	2
P

联想：（1）一个袋子里装有大小相同的3个红球和2个白球，从中同时取出2个球，则其中含有红球个数η的概率分布是

η	0	1	2
P

　　

（2）四个纪念章A、B、C、D，投掷时正面向上的概率如下表所示，这四个纪念章同时投掷时，出现

纪念章	A	B	C	D
概　率			a	a(0<a<1)

　　　n个正面的概率记作P_n。（Ⅰ）求概率P_i (i=0 , 1 , 2 , 3 , 4 )

　　　（Ⅱ）求在概率P_i中P₂为最大时，a的取值范围。

　　 （3）5个身高均不相同的学生排成一排合影留念，高个子站在中间，从中间到左边一个比一个矮，从中间到右边也一个比一个矮，则这样的排法有 （　 ）

　　　A．6种　　　　　 B．8种　　　　  C．12种　　　　  D．16种

9．椭圆（a>b>0）的半焦距为c，若直线y=2x与椭圆一个交点的横坐标恰为

c，则椭圆的离心率为（　）

　A．　　　 B．　　　　C．　　　　 D．

联想：（1）若椭圆的离心率是，则实数a的值为　　　　  。

　　 （2）椭圆上有n个不同的点P₁、P₂、…、P_n，椭圆的右焦点为F，数列｛｝是公差大于的等差数列，则n的最大值为

　　　A．199　　　　　 B．200　　　　　 C．198　　　　  D．201

　　 （3）若将离心率为的椭圆（a>b>0）绕着它的左焦点按逆时针方向旋转后，所得新椭圆的一条准线方程是3y+14=0，则新椭圆的另一条准线方程是（　）

　　 A．3y－14=0　　　 B．3y－23=0　　　C．3y－32=0　　　 D．3y－50=0

10．已知函数f ( x )=，给出下列命题：①f ( x )必是偶函数；②f ( 0 )=

f ( 2 )时f ( x )的图象必关于直线x=1对称；③若a²－b≤0则f ( x )在区间上是增函数；

④f ( x )有最大值，其中正确命题的序号是　　　　  。

联想：（1）设函数f ( x )=lg ( x² +ax－a－1)给出下述命题：①f ( x )有最小值；②当a=0时，f ( x )的值域为R；③当a>0时，f ( x )在区间上有反函数；④若f ( x )在区间上单调递增，则实数a的取值范围是a≥－4，其中正确的命题是　　　　　　　　　 。

　　 （2）定义在R上的偶函数f ( x )，且f ( x+1 )=－ f ( x )，f ( x )在[0，1]上是增函数，关于f ( x )的判断：①f ( x )是周期函数；②f ( x )的图象关于直线x=1对称；③f ( x )在[－1，0]上是增函数；④f ( x )在[1，2]上是减函数；⑤f ( 0 )= f ( 2 )，则正确命题的序号是　　　　　  。

11．曲线y=x³－3x上切线平行于x轴的交点的坐标是（　　）

　A．（－1，2）　　　 B．（1，－2）　　  C．（1，2）　　  D．（－1，2）或（1，－2）

联想：（1）若函数f ( x )=ax³ + bx² + cx + d（a>0）在R上为增函数，则

　　　A．b²－3ac>0　　　 B．b<0 , c>0　　　 C．b=0 , c>0　　　　D．b²－3ac<0

　　 （2）已知函数f ( x )=x³ + ax² + bx + c在x=－与x=1处都取得极值，若在[－1，2]时f ( x )< c²恒成立，则实数c的取值范围是　　　　　　　　 .

　　 （3）函数f ( x )=ax³ + bx在x=1处有极值－2，点P是函数图象上任意一点，过P的切线的倾斜角为α，则α的取值范围是　　　　　　　 。

　　 （4）抛物线C₁：y=3x²和C₂：y=－x² + 4tx交于原点O和点A，过点A作C₂的切线 ,它与C₁相交于点P，当t在实数范围内变化时，求线段AP的中点M的轨迹方程，并说明轨迹是什么图形？

【参考答案】

联想与激活（3）

1．C 联想：（1）2⁵　　　　  （2）2¹⁵－1　　　　　　 （3）D

2．C 联想：（1）C　　　　  （2）A　　　　　  （3）A　　　　　  （4）A

3．A 联想：（1）D　　　　  （2）5　　　　　　 （3）0　　　　　  （4）

4．B 联想：（1）D　　　　  （2）②　　　　　　 （3）B　

5．A 联想：（1）　　　　（2）　　　　　　 （3）　　　　 （4）

6．A 联想：（1）C　　　　  （2）C　　　　　　　 （3）C　

7． 联想：（1）4　　　　（2）24　　　　  （3）A

8．B 联想：（1）80　　　　  （2）0或5　　　　 （3）　　

9．B 联想：（1）A　　　　  （2）B　  

10．C 联想：（1）　　　　（2）B　　

11．n = 7 , z = 3330　解：当n = I时，x = 1＋2i　y = 2ⁱ　

数列｛x_a｝是A·P　 ｛y_n｝是G·P　　x₀ = 1　,  y₀ = 1

z_i－z₀ = 　估算知当i≤7时， z≤7000　　 故n = 7 , z = = 3330

联想：（1）（Ⅰ）a_n＋1 = ①　　2a_n＋2 = ②

②－①得2a_n＋2­－a_n＋1 =

即b_n＋1 = 　　 ∴为常数　　即｛b_n｝为G·P

（Ⅱ）a_n＋1 =  

= 　

=

= … =

=  =

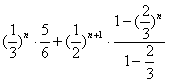即｛a_n｝通项公式为a_n =

（Ⅲ）a_n =

　　 　　　 = 3－1 = 2

12.解：（I）由题知AD⊥DB，CB⊥BD。又二面角A—DB—C为90°， ∴AD、BC成角为

90°。

（II）作PE⊥CD于E，DF⊥DB于F，可知F为P在面DBC内的射影，∴EF⊥CD　二面角P—DC—B的平面角即为∠PEF，当∠PEF=45°时，PF=EF，设PB=BA，则PF=a，DF=（1－）a，EF=　　∴=　 ∴当PB=（2－）a时，△PCD与△BCD所在平面成45°

（III）取AB、DC中点F，E，取点O使OE⊥面BCD及OF⊥AB，则O为所求圆心知r =OC=　　故S=4r²=3a²

联想与激活（4）

1．B　　联想：（1）A　 （2）a≤4　  （3）A　　（4）C

2．D　　联想：（1）B　 （2）D　　　 （3）C　　（4）D　　（5）B

3．D　　联想：（1）B　　（2）y=cos(x+)　　　（3）D

4．D　　联想：（1）A　　（2）A　　（3）A　　（4）B

5．D　　联想：（1）C　　 （2）B

6．D　　联想：（1）A　　 （2）B　　（3）①③②④　　②③①④

7．双曲线　 y=在第一象限内部分

联想：（1）B　　 （2）B　　 （3）41

8．0.9025，0.095，0.0025

联想：（1）

（2）（I）P₀=(1－a)²　　　P₁=(1－a)²+a(1－a)= (1－a)

　　　　 P₂=(1－a)²+a²+4·a(1－a)= (－2a²+2a+1)

　　　　 P₃=a²+a(1－a)= a　　　 P₄=a²

（II）∵0＜a＜1，P₀＜P₁，P₄＜P₃，

P₂－P₁=－≥0，P₂－P₃=－(2a²－1)≥0，

∴　 2a²－4a+1≤0　　　∴　

　 　2a²－1≤0　　　　　　 

∴

（3）A

9．D　　联想：（1）4或－　　　　  （2）A　　　 （3）D

10．③　　联想：（1）②③　　　　（2）①②④⑤

11．D

联想：（1）D　　　（2）c＞2或c＜－1

解：f′(x)=3x²+2ax+b　由题意知，，1是方程f′(x)=0的二根

∴+1=－　且　 ×1=　 ∴a=－,b=－2　 ∴f′(x)=3(x+)(x－1)

∴f (x)在增，减，增　

g(2)=2,g(1)=－ 　　g(－1)=　 g(－)＜0

c²－c＞x³－x²－2x=g(x)　　∴c²－c＞[g(x)]_max　

∴[g(x)]_max=2　　∴c²－c＞2　　∴c＞2或c＜－1

（3）

解：f′(x)=3ax²+b　　∴f′(1)=0且f (1)=－2

∴ 3a+b=0　　　∴ a=1　　　 

　 a+b=－2 　　　 b=－3

∴f (x)=x³－3x　　∴f′(x)=3x²－3≥－3　　 ∴tanα≥－3　 ∴0≤α＜或≤α＜（4）A(t,3t²)　　　L_AP：y=2tx+t²　　 P()

解：M()　 ∴M轨迹为y=15x²是抛物线