六、平面向量
考试要求:1、理解向量的概念,掌握向量的几何表示,了解共线向量的概念。2、掌握向量的加法和减法。3、掌握实数与向量的积,理解两个向量共线的充要条件。4、了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。5、掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直问题,掌握向量垂直的条件。6、掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用,掌握平移公式。
1、已知向量![]() 不共线,且
不共线,且![]() ,则下列结论中正确的是
,则下列结论中正确的是
A.向量![]() 垂直 B.向量
垂直 B.向量![]() 与
与![]() 垂直
垂直
C.向量![]() 与
与![]() 垂直 D.向量
垂直 D.向量![]() 共线
共线
2.已知在△ABC中,![]() ,则O为△ABC的
,则O为△ABC的
A.内心 B.外心 C.重心 D.垂心
3.在△ABC中设![]() ,
,![]() ,点D在线段BC上,且
,点D在线段BC上,且![]() ,则
,则![]() 用
用![]() 表示为
。
表示为
。
4、已知![]() 是两个不共线的向量,而
是两个不共线的向量,而![]() 是两个共线向量,则实数k = .
是两个共线向量,则实数k = .
5、设![]() 、
、![]() 是平面直角坐标系内分别与
是平面直角坐标系内分别与![]() 轴、y轴方向相同的两个单位向量,且
轴、y轴方向相同的两个单位向量,且![]() ,
,![]() ,则△OAB的面积等于 :
,则△OAB的面积等于 :
A.15 B.10 C.7.5 D.5
6、已知向量![]() ,则向量
,则向量![]() 的坐标是
,
的坐标是
,
将向量![]() 按逆时针方向旋转90°得到向量
按逆时针方向旋转90°得到向量![]() ,则向量
,则向量![]() 的坐标是
.
的坐标是
.
7、已知![]() ,则下列k值中能使△ABC是直角三角形的值是
,则下列k值中能使△ABC是直角三角形的值是
A.![]() B.
B.![]() C.-5 D.
C.-5 D.![]()
8、在锐角三角形ABC中,已知![]() 的面积为
的面积为![]() ,则
,则![]()
,![]() 的值为
.
的值为
.
9、已知四点A ( – 2,1)、B (1,2)、C (
– 1,0)、D (2,1),则向量![]() 与
与![]() 的位置关系是
的位置关系是
A. 平行 B. 垂直 C. 相交但不垂直 D. 无法判断
10、已知向量![]() 夹角的范围是:
夹角的范围是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、若![]() 则
则![]() 等于:
等于:
A.5 B.![]() C.
C.![]() D.
D.![]()
12、已知![]() =(6,2),
=(6,2),![]() =
=![]() ,直线l过点A
,直线l过点A![]() ,且与向量
,且与向量![]() 垂直,则直线
垂直,则直线
l的一般方程是 .
13、设![]() 是函数
是函数![]() 的单调递增区间,将
的单调递增区间,将![]() 的图象按
的图象按![]() 平移得到一个新的函数
平移得到一个新的函数![]() 的图象,则
的图象,则![]() 的单调递减区间必是:
的单调递减区间必是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14、把函数![]() 的图象按向量
的图象按向量![]() 平移,得到函数
平移,得到函数![]() 的图象,则
的图象,则![]() 为 ( )
为 ( )
A.(3,-4) B.(3,4) C.(-3,4) D.(-3,-4)
15、如果把圆![]() 平移后得到圆C′,且C′与直线
平移后得到圆C′,且C′与直线![]() 相切,则m的值为
.
相切,则m的值为
.
16、已知P是抛物线![]() 上的动点,定点A(0,-1),若点M分
上的动点,定点A(0,-1),若点M分![]() 所成的比为2,则点M的轨迹方程是_____,它的焦点坐标是_________.
所成的比为2,则点M的轨迹方程是_____,它的焦点坐标是_________.
17、若D点在三角形的BC边上,且![]() ,则
,则![]() 的值为:
的值为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
18、若向量![]() 则
则![]() 一定满足:
一定满足:
A.![]() 的夹角等于
的夹角等于![]() B.
B.![]() C.
C. ![]() D.
D.![]()
19、已知A(3,0),B(0,3),C(cos![]() ,sin
,sin![]() ).
).
(1)若![]() =-1,求sin2
=-1,求sin2![]() 的值;
的值;
(2)若![]() ,且
,且![]() ∈(0,π),求
∈(0,π),求![]() 与
与![]() 的夹角.
的夹角.
20、已知O为坐标原点,![]() 是常数),若
是常数),若![]() (Ⅰ)求y关于x的函数解析式
(Ⅰ)求y关于x的函数解析式![]() (Ⅱ)若
(Ⅱ)若![]() 时,
时,![]() 的最大值为2,求a的值并指出
的最大值为2,求a的值并指出![]() 的单调区间.
的单调区间.
21、已知A(-2,0)、B(2,0),点C、点D满足![]()
(1)求点D的轨迹方程;
(2)过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为![]() ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.
22、如图,已知△OFQ的面积为S,且 ![]() .
.
(1)若![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
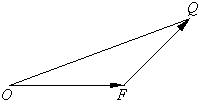 (2)设
(2)设![]() = c(c≥2),S =
= c(c≥2),S =![]() ,若以O为中心,F为焦点的椭圆经过点Q,当
,若以O为中心,F为焦点的椭圆经过点Q,当![]() 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.
六、平面向量参考答案
1、A;2、D;3、![]() ;4、
;4、![]() ;5、D;6、
;5、D;6、![]() ,
,![]() ;7、D;
;7、D;
8、![]() , 2;9、A;10、C;11、D;12、
, 2;9、A;10、C;11、D;12、![]() ;13、D;14、D;15、
;13、D;14、D;15、![]() ;
;
16、![]() ,
,![]() ;17、C;18、B
;17、C;18、B
19(1)解:![]() ,
,![]()
∴![]() =-1
=-1![]()
![]()
∴![]() ,∴
,∴![]() ∴
∴![]()
(2)∵![]() ,∴
,∴![]()
化简得![]() , ∵
, ∵![]() , ∴
, ∴![]()
∴![]() =
=![]()
∴![]() 与
与![]() 的夹角为
的夹角为![]()
20.(1)![]()

21.解:(I)设C、D点的坐标分别为C(![]() ,D
,D![]() ,则
,则![]() ),
),![]()
则![]() ,故
,故![]()
又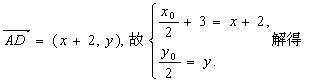
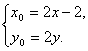
代入![]() 得
得![]() ,即为所求点D的轨迹方程.
,即为所求点D的轨迹方程.
(II)易知直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的方程为
的方程为![]() ①.
①.
又设椭圆方程为![]() ②.
②.
因为直线![]() 与圆
与圆![]() 相切.故
相切.故![]() ,解得
,解得![]()
将①代入②整理得,![]() ,
,
而![]() ,即
,即![]() ,设M(
,设M(![]() ,N(
,N(![]() ,则
,则![]() ,由题意有
,由题意有![]() ,求得
,求得![]() .经检验,此时
.经检验,此时![]()
故所求的椭圆方程为![]()
22.解:(1)由已知,得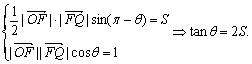
∵![]() <S<2,∴2<tan
<S<2,∴2<tan![]() <4,则
<4,则![]() <
<![]() <arctan4.
<arctan4.
(2)以O为原点,![]() 所在直线为x轴建立直角坐标系,设椭圆方程为
所在直线为x轴建立直角坐标系,设椭圆方程为![]() (a>0,b>0),Q的坐标为(x1,y1),则
(a>0,b>0),Q的坐标为(x1,y1),则![]() =(x1-c,y1),
=(x1-c,y1),
∵△OFQ的面积为![]() ∴y1 =
∴y1 =![]()
又由![]() ·
·![]() =(c,0)·
=(c,0)·![]() =(x1-c)c =
1,
=(x1-c)c =
1,
得x1 =![]() (c≥2).
(c≥2).
当且仅当c
= 2时![]() 最小,此时Q的坐标为
最小,此时Q的坐标为![]() ,
,
由此可得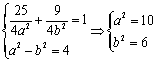 , 故椭圆方程为
, 故椭圆方程为![]() .
.