高考数学复习平面向量测试题
一、平面向量的实际背景与基本概念
1．（人教版P85例2）
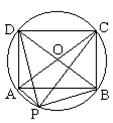
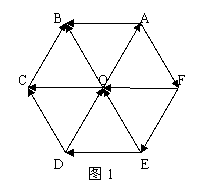
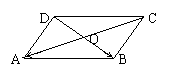
如图1，设O是正六边形的中心，分别写出
图中与
、
、
相等的向量。
变式1：
如图1，设O是正六边形的中心，分别写出
图中与
、
共线的向量。
解：
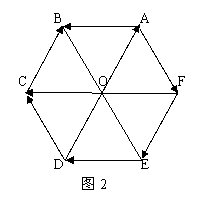
变式2：
如图2，设O是正六边形的中心，分别写出
图中与
的模相等的向量以及方向相同的向量。
解：
二、平面向量的线性运算
2.（人教版第96页例4）
如图，在平行四边形ABCD中，
a ，
b ，
你能用a，b表示向量 
，
吗？
变式1：如图，在五边形ABCDE中，
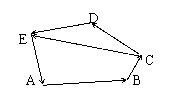
a ，
b ，
c ，
d ，
试用a ，b ， c ， d表示向量
和
.
解：
( a
+ b + d )
( d + a +
b +c )
变式2：如图，在平行四边形ABCD中，若，
a ，
b
则下列各表述是正确的为（ ）
A．
B．
C．
a + b D．
(a + b)
正确答案：选D
变式3：已知
=a，
=b, 
=c,
=d, 且四边形ABCD为平行四边形，则（ ）
A. a+b+c+d=0 B. a－b+c－d=0
C. a+b－c－d=0 D. a－b－c+d=0
正确答案：选A
变式4：在四边形ABCD中，若
，则此四边形是( )
A．平行四边形 B．菱形 C．梯形 D．矩形
正确答案：选C
变式5：已知a、b是非零向量，则a=b是(a+b)与(a－b)垂直的 （ ）
A．充分但不必要条件 B．必要但不充分条件
C．充要条件 D．既不充分也不必要条件
正确答案：选C
变式6：在四边形ABCD中，
=a+2b，
=－4a－b，
=－5a－3b，其中a、b不共线，则四边形ABCD为（ ）
A.平行四边形 B.矩形 C.梯形 D.菱形
【解析】 ∵
=
=－8a－2b=2，∴
.
∴四边形ABCD为梯形.
正确答案：选C
变式7：已知菱形ABCD，点P在对角线AC上（不包括端点A、C），则
等于（ ）
A.λ(+),λ∈(0,1) B.λ(+),λ∈(0,
)
C.λ(－),λ∈(0,1) D.λ(
),λ∈(0,)
【解析】 由向量的运算法则
=+，而点P在对角线AC上，所以与同向，且＜,∴=λ(+),λ∈(0,1).
正确答案：选 A
变式8：已知D、E、F分别是△ABC的边BC、CA、AB的中点，且=
，
=
，=
,则下列各式： ①
=
－ ②
= +
③
=－ + ④++=
其中正确的等式的个数为（ ）
A.1 B.2 C.3 D.4
正确答案：选B
3．（人教版第98页例6）
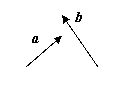如图，已知任意两个非零向量a 、b ，试作a + b，a + 2b，
a + 3b，你能判断A、B、C三点之间的位置关系吗？为什么？
变式1：已知a + 2b，2a + 4b，3a + 6b (其中a 、b是两个任意非零向量) ，证明：A、B、C三点共线．
证明：∵
a + 2b，
2a + 4b，
∴ 
所以，A、B、C三点共线．
变式2：已知点A、B、C在同一直线上，并且a + b，
a + 2b，
a + 3b (其中a 、b是两个任意非零向量) ，试求m、n之间的关系．
解：
a + b ，
a + 2b
由A、B、C三点在同一直线上可设
，
则 
所以 
即 
为所求．
4．（人教版第102页第13题）
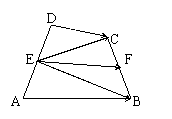已知四边形ABCD，点E、F、G、H分别是AB、BC、CD、DA的中点，求证：
变式1：已知任意四边形ABCD的边AD和BC的中点分别为E、F，
求证：
.
证明：如图，连接EB和EC ，
由
和
可得，
（1）
由
和
可得，
（2）
（1）+（2）得， 
（3）
∵E、F分别为AD和BC的中点，∴
，
，
代入（3）式得，
三、平面向量的基本定理及坐标表示
2.（人教版第109页例6）
已知a = (4，2)，b = (6，y)，且a // b ，求 y ．
变式1：与向量a = (12，5) 平行的单位向量为（ ）
A．
B．
C．
或 D．
或
正确答案：选C
变式2：已知a
，b
，当a+2b与2a－b共线时，
值为 （ ）
A．1
B．2
C．
D．
正确答案：选D
变式3：已知A(0,3) 、B(2,0) 、C(－1,3)
与
方向相反的单位向量是( )
A．(0,1) B．(0,－1) C． (－1,1) D．(1,－1)
正确答案：选A
变式4：已知a = (1，0)，b = (2，1) ．试问：当k为何实数时， ka－b与a+3b平行, 平行时它们是同向还是反向？
解：因为 ka－b 
，a+3b
．
由已知得，
解得 
，
此时，ka－b 
，a+3b，二者方向相反．
2.（人教版第110页例8）
设点P是线段
上的一点，
、
的坐标分别为
，
．
(1) 当点P是线段上的中点时，求点P的坐标；
(2) 当点P是线段的一个三等分点时，求P的坐标
变式1：已知两点
，
，
，则P点坐标是 （ ）
A．
B．
C．
D．
正确答案：选B
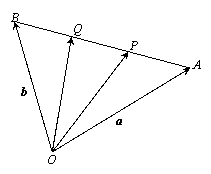变式2：如图，设点P、Q是线段AB的三等分点，
若
＝a，
＝b，则
＝ 
，
＝ 
(用a、b表示)
四、平面向量的数量积
5．（人教版第116页例3）
已知a＝6，b ＝4且a与b的夹角为
，求
(a + 2b)·(a
b) ．
变式1：已知
那么与夹角为
A、
B、
C、
D、
正确答案：选C
变式2：已知向量a和b的夹角为60°， a ＝ 3， b ＝ 4，则（2a – b）·a等于
（A）15 （B）12 （C）6 （D）3
正确答案：选B
变式3：在△ABC中，已知=4，=1，S△ABC=
，则·等于（ ）
A.－2 B.2 C.±2 D.±4
正确答案：选C
变式4：设向量
与向量
的夹角为钝角，求实数t的取值范围.
解：∵
，故
，
解之
．
另有
，解之
，
∴
．
2.（人教版第116页例4）
已知a＝3，b ＝4且a与b不共线，k为何实数时，向量a + kb 与a
b互相垂直？
变式1：已知a⊥b ，a＝2，b ＝3，且向量3a + 2b与ka
b互相垂直，则k的值为（ ）
A．
B．
C．
D．1
正确答案：选B
变式2：已知a＝1，b
＝
且（a－b）⊥a，则a与b夹角的大小为 45º ．
解：
2.（人教版第119页 第11题）
已知a = (4，2)，求与向量a 垂直的单位向量的坐标．
变式1：若i = (1,0), j =(0,1)，则与2i+3j垂直的向量是 ( )
A．3i+2j B．－2i+3j C．－3i+2j D．2i－3j
正确答案：选C
变式2：已知向量
，
，若
与
垂直，则实数
=（ ）
A．1 B．－1 C．0 D．2
正确答案：选B
变式3：若非零向量
互相垂直，则下列各式中一定成立的是 （ ）
A．
B．
C．
D．
正确答案：选B
变式4：已知向量a＝（3，－4），b＝（2，x）， c＝（2，y）且a∥b，a
c．求b－c的值．
解：∵ a∥b，∴ 3x＋8＝0．
∴x＝
． ∴ b＝（2，
） ．
∵
ac，
∴ 6－4y＝0． ∴ y＝． ∴ c＝（2，
）．
而b－c ＝（2，）－（2，）＝（0，－
），
∴ b－c＝．
（人教版第118页例5）
已知A (1，2)，B (2，3)，C (
，5)，试判断
的形状，并给出证明．
变式1：
是所在的平面内的一点，且满足
，则 一定为（ ）
A．正三角形 B．等腰直角三角形 C．直角三角形 D．斜三角形
正确答案：选C
变式2：已知A、B、C三点不共线，O是△ABC内的一点，若＋＋＝0，
则O是△ABC的（ ）
A． 重心 B． 垂心 C． 内心 D． 外心
正确答案：选A
变式3：已知
，则△ABC一定是 （ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰直角三角形
正确答案：选B
变式4：四边形
中，
（1）若
，试求与
满足的关系式；
（2）满足（1）的同时又有
，求
的值及四边形的面积。
解：
（1）
则有
化简得：
（2）
又 则 
化简有：
联立
解得
或
则四边形为对角线互相垂直的梯形
当 
此时
当 
此时
五、平面向量应用举例
（人教版第121页 例1）
题目意图：用平面向量的方法证明平面几何命题：平行四边形两条对角线的平方和等于其两条邻边的平方和的两倍
变式1：如图，矩形ABCD内接于半径为r的圆O，点P是圆周上任意一点，
|
证明：
，
，
，
，
以上各式相加可证．
变式2：已知△ABC中，
，若
，求证：△ABC为正三角形.
证明：
， ∴
， 又∵
， 
，
故
， 知a=b， 同理可知b=c
， 故a=b=c ， 得证．
变式3：已知平行四边形ABCD的两条对角线AC与BD交于E，O是任意一点，求证
.
【证明】 ∵E是对角线AC与BD的交点，∴
.
在△OAC中，
，
同理有
.
四式相加可得：.
变式4：四边形ABCD的边AD和BC的中点分别为E、F，
求证：
【证法一】 ∵E、F分别为DA、BC的中点.
∴
又∵
=0①
=0②
①+②，得2
=0
∴2
∴
【证法二】 连结EC，EB
∵
，①
②
①+②,得2+0=
，
∴
又∵
③
④
③+④,得
又∵
=0，
∴.