高考数学二模选填题专项练习
1.若![]() 且
且![]() ,则
,则![]() 的最大值为
( )
的最大值为
( )
![]()
2.如果![]() 为偶函数,且导数
为偶函数,且导数![]() 存在,则
存在,则![]() 的值为
( )
的值为
( )
A.2 B.1 C.0 D.-1
3. 直线![]() 必过定点
(
)
必过定点
(
)
A.![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
4. 设函数![]() 为奇函数,
为奇函数,![]() ,
,![]() ,则
,则![]() =( )
=( )
A. ![]() B.
1 C.
B.
1 C. ![]() D. 5
D. 5
5. 半径为R的球内接正四面体的全面积为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.
已知不等式![]() 对任意正实数x,y恒成立,则正实数a的最小值是( )
对任意正实数x,y恒成立,则正实数a的最小值是( )
A.2 B.4 C.6 D.8
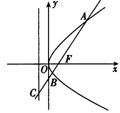
7.定点N(1,0),动点A、B分别在图中抛物线![]() 及椭圆
及椭圆![]()
的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是( )
 A.(
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
 9.
9.
10.已知函数![]() .若实数
.若实数![]() 使
使
得![]() 有实根,则
有实根,则![]() 的最小值为
( )
的最小值为
( )
(A) ![]() (B)
(B)![]() (C) 1 (D)2
(C) 1 (D)2
11. 若定义在![]() 上的不恒为零的函数
上的不恒为零的函数![]() ,满足
,满足![]() ,当
,当![]() 时,
时,![]() ,则,当
,则,当![]() 时,必有( )
时,必有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12. 设M是![]()
m、n、p分别是![]() 的最小值是 ( )
的最小值是 ( )
A.8 B.9 C.16 D.18
13. 若数列![]() 的前8项的值互异,且
的前8项的值互异,且![]() 对任意的
对任意的![]() 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍![]() 的前8项值的数列为( )
的前8项值的数列为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
14. 定义一种运算“*”,对正整数n满足以下等式:①1*1=1;②(n+1)*1=3(n*1),则n*1
=( )
A.3n nnnnj jjj B.3n-1 C.![]() D.
D.![]()
15. 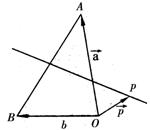 如图,
如图,![]() 是平面上三点,向量
是平面上三点,向量![]()
![]() ,
,![]()
![]() .
.
在平面![]() 上,
上,![]() 是线段
是线段![]() 垂直平分线上任意一点,
垂直平分线上任意一点,
向量![]() =
=![]() ,且
,且![]() 则
则 ![]() 的值是:
的值是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16. 当![]() 、
、![]() 满足条件
满足条件![]() 时,变量
时,变量![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.编辑一个运算程序:1&1 = 2 , m & n = k , m & (n + 1) = k + 2,则 1 & 2006 的输出
结果为
A.4006 B.4008 C.4010 D.4012
18. 过双曲线![]() 的左焦点
的左焦点![]() ,作圆
,作圆![]() 的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是(
)
的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]() 大小不定
大小不定
19.如果 (sinx) ′=cosx , (cosx) ′=-sinx,设 f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2006(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
20. 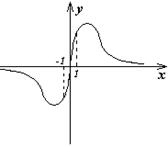 若函数
若函数![]() 的图象如图所示,则m的取值范围为
的图象如图所示,则m的取值范围为
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
21. 定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时
时![]() ,则当
,则当![]() 时,
时,![]() 的最小值是
( )
的最小值是
( )
A. -1 B.![]() C.
C.![]() D.
D.![]()
22. 在数列![]() 中,如果存在非零常数
中,如果存在非零常数![]() ,使得
,使得![]() 对于任意的非零自然数
对于任意的非零自然数![]() 均成立,那么就称数列
均成立,那么就称数列![]() 为周期数列,其中
为周期数列,其中![]() 叫数列
叫数列![]() 的周期。已知数列
的周期。已知数列![]() 满足
满足![]() ,如果
,如果![]() ,当数列
,当数列![]() 的周期最小时,该数列前2005项的和是
( )
的周期最小时,该数列前2005项的和是
( )
A.668 B.669 C.1336 D.1337
23. 已知点Q(2![]() ,0)及抛物线y=
,0)及抛物线y=![]() 上一动点P(x,y),则y+PQ的最小值是( )
上一动点P(x,y),则y+PQ的最小值是( )
A、2 B、3 C、4 D、2![]()
24. 正方体的八个顶点中任取四个顶点构成三棱锥的概率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
25. 若a>3, 则方程x3-ax2+1=0在(0, 2)上恰有( )
A、0个根 B、1个根 C、2个根 D、3个根
26. 使关于![]() 的不等式
的不等式![]() 有解的实数
有解的实数![]() 的取值范围是 (
):
的取值范围是 (
):
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
27. 设函数![]() 的定义哉为实数集R,如果存在实数
的定义哉为实数集R,如果存在实数![]() ,使得
,使得![]() ,那么
,那么![]() 为函数
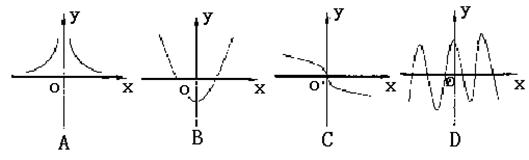
为函数![]() 的不动点,下列图像中表示有且只有两个不动点的函数图像是( )
的不动点,下列图像中表示有且只有两个不动点的函数图像是( )
|
28.当a为任意实数时,直线![]() 恒过定点P,则过点P的抛物线的标准方程是 ( )
恒过定点P,则过点P的抛物线的标准方程是 ( )
A.![]() B.
B.![]()
C.![]()
![]() D.
D. ![]()
29. 如果以原点为圆心的圆经过双曲线![]() 的焦点,并且被直线
的焦点,并且被直线![]() 为双曲线的半焦距)分为弧长为2:1的两段弧,则该双曲线的离心率等于( )
为双曲线的半焦距)分为弧长为2:1的两段弧,则该双曲线的离心率等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
30.函数![]() 是定义在R上的增函数,
是定义在R上的增函数,![]() 的图象经过(0,-1)和下面哪一个点时,能使不等式
的图象经过(0,-1)和下面哪一个点时,能使不等式![]() 的解集是
的解集是![]() ( )
( )
A.(3,2) B.(4,0) C.(3,1) D.(4,1)
31.已知![]() 有实根,则a与b夹角的取值范围是 ( )
有实根,则a与b夹角的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
32.在直角三角形ABC中,∠C=90°,那么sinA·cos2(45°-![]() 为 ( )
为 ( )
A.有最大值![]() 和最小值0 B.有最大值
和最小值0 B.有最大值![]() ,但无最小值
,但无最小值
C.既无最大值也无最小值 D.有最大值![]() ,但无最小值
,但无最小值
33. 12.2002年8月,在北京召开了国际数学家大会,大会会标为右图所示,它是由四个相同的直角三角形与中间的一个小正方形拼成一个大正方形,若直角三角形中较大的锐角为![]() ,大正方形的面积为1,小正方形的面积为
,大正方形的面积为1,小正方形的面积为![]() ,则sin2
,则sin2![]() -cos2
-cos2![]() 的值等于 ( )
的值等于 ( )
 A.1 B.
A.1 B.![]()
C.![]() D.-
D.-![]()
34.设![]() ,实数x、y满足条件
,实数x、y满足条件![]() 则
则![]() 的最大值是( )
的最大值是( )
A.![]() B.3 C.4 D.5
B.3 C.4 D.5
35.对于直角坐标系内任意两点![]() 、
、![]() ,定议运算
,定议运算
![]()
![]() ,若M是与原点相异的点,且
,若M是与原点相异的点,且![]() 则
则![]() 等于 ( )
等于 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
36.
|
A.6种 B.8种
C.36种 D.48种
37.已知函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中对于
.其中对于![]() 定义域内的任意一个自变量
定义域内的任意一个自变量![]() 都存在唯一个个自变量
都存在唯一个个自变量![]() =3成立的函数是 ( )
=3成立的函数是 ( )
A.①②④ B.②③ C.③ D.④
38.已知函数![]() 的定义域是
的定义域是![]()
![]() 值域是
值域是![]() ,则满足条件的整数数对
,则满足条件的整数数对![]() 共有
( )
共有
( )
A.2个 B.5个 C.6个 D.无数个
39.已知函数![]() 的图像上,相邻的一个最大值点与一个最小值点恰好都在圆
的图像上,相邻的一个最大值点与一个最小值点恰好都在圆![]() 上,则
上,则![]() 的最小正周期为 ( )
的最小正周期为 ( )
A.4 B.3 C.2 D.1
40.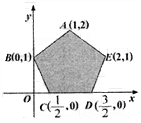 已知以
已知以![]() 为自变量的目标函数
为自变量的目标函数![]() 的可行域
的可行域
如图阴影部分(含边界),若使![]() 取最大值时的最优解有无穷
取最大值时的最优解有无穷
多个,则k的值为 【 】
A.1 B.![]() C.2 D.4
C.2 D.4
41.已知实数x、y满足![]()
![]() 的最大值为---- ----------------( )
的最大值为---- ----------------( )
A.![]() B.
B.![]() C.6 D.12
C.6 D.12
42.3.分别写有![]() 的九张卡片中,任意抽取两张,当两张卡片上的字之和能被3整除时,就说这次试验成功,则一次试验成功的概率为 ( )
的九张卡片中,任意抽取两张,当两张卡片上的字之和能被3整除时,就说这次试验成功,则一次试验成功的概率为 ( )
![]()
![]()
![]()
![]()
43.
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
1.已知的最小![]() 值是 .
值是 .
2.过抛物线![]() 与抛物线交于A、B两点,且△OAB(O为坐标原点)的面积为
与抛物线交于A、B两点,且△OAB(O为坐标原点)的面积为![]() =
=
3.已知函数f(x)满足:![]() +
+
![]() .
.
4.已知点P(x,y)的坐标满足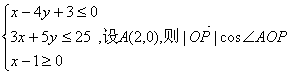 (O为坐标原点)的最大值为 .
(O为坐标原点)的最大值为 .
5.已知F1、F2分别是双曲线![]() 的左、右焦点,P为双曲线左支上任意一点,若
的左、右焦点,P为双曲线左支上任意一点,若![]() 的最小值为8a,则该双曲离心率e的取值范围是
.
的最小值为8a,则该双曲离心率e的取值范围是
.
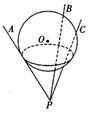 6.如图是个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两
6.如图是个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两
夹角都是60°,一个半径为1的球放在支架上,则球心O到P的
距离是 .
7.函数![]() 的图象和函数
的图象和函数![]() 的图象关于直线
的图象关于直线
![]() 对称,则直线
对称,则直线![]() 的方程是
。
的方程是
。
8.对任意两个集合![]() ,定义
,定义![]() ,
,
![]() 设
设![]() ,
,![]() ,则
,则![]() __ __
__ __
9.编辑一个运算程序:![]() ,
,![]() ,
,![]() ,欲得到
,欲得到![]() 的输出结果,则
的输出结果,则![]() 的值为 。
的值为 。
10.设双曲线![]() 的右焦点为F,右准线
的右焦点为F,右准线![]() 与两条渐线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= 。
与两条渐线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= 。
11.已知实数![]() 满足
满足![]() ,则
,则![]() 的最小值为
;
的最小值为
;
12.对于任意实数x , y ,定义运算![]() ,其中a,
b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*
m=x,则m=
.
,其中a,
b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*
m=x,则m=
.
13.某公司欲投资13亿元进行项目开发,现有下6个项目可供选择;
| 项目 | A | B | C | D | E | F |
| 投资额/亿元 | 5 | 2 | 6 | 4 | 6 | 1 |
| 利润/亿元 | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 0.1 |
设计一个投资方案,使投资13亿元所获利润大于1.6亿元,则应选的项目是 .(只需写出项目的代号)
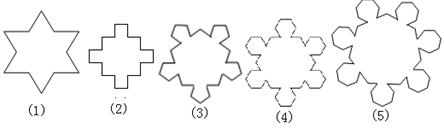
14.如下图,第(1)个多边形是由正三角形“扩展“而来,第(2)个多边形是由正四边形“扩展”而来,……如此类推.设由正![]() 边形“扩展”而来的多边形的边数为
边形“扩展”而来的多边形的边数为![]() ,
,
则![]()
![]() ;
; ![]() =
.
=
.
15.已知![]() 为正数,且满足
为正数,且满足![]() ,则
,则![]() 的最大值是_____.
的最大值是_____.
16.在![]() 中,若
中,若![]() ,则
,则![]() .
.
17.已知函数![]() ,
,![]() ,直线
,直线![]() 与
与![]() 、
、![]() 的图象分别交于
的图象分别交于![]() 、
、![]() 点,则
点,则![]() 的最大值是 _ .
的最大值是 _ .
18.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是①三角形 ②菱形 ③矩形 ④正方形 ⑤正六边形,其中正确的序号是_________
19.设椭圆![]() 的右焦点为F,C为椭圆短轴上端点,向量
的右焦点为F,C为椭圆短轴上端点,向量![]() 绕F点顺时针旋转
绕F点顺时针旋转![]() 后得到向量
后得到向量![]() ,其中
,其中![]() 恰好在椭圆右准线上,则该椭圆的离心率为________
恰好在椭圆右准线上,则该椭圆的离心率为________
20.有一公用电话亭,在观察使用这个电话的人的流量时,设在某一个时刻,有n个人正在使用电话或等待使用的概率为![]() ,且
,且![]() 与时刻t无关,统计得到
与时刻t无关,统计得到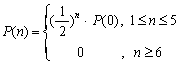 ,那么在某一时刻这个公用电话亭里一个人也没有的概率P(0)的值是 .
,那么在某一时刻这个公用电话亭里一个人也没有的概率P(0)的值是 .
21.对于各数互不相等的整数数组![]() (n是不小于2的正整数),如果在
(n是不小于2的正整数),如果在![]() 时有
时有![]()
![]()
![]() ,则称
,则称![]() 与
与![]() 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”。例如,数组(2,4,3,1)中有逆序“2,1”,“4,3”,“4,1”,“3,1”,其“逆序数”等于4。若各数互不相等的正整数数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”。例如,数组(2,4,3,1)中有逆序“2,1”,“4,3”,“4,1”,“3,1”,其“逆序数”等于4。若各数互不相等的正整数数组![]() 的“逆序数”是2,则
的“逆序数”是2,则![]() 的“逆序数”是__________.
的“逆序数”是__________.
22.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格点函数。下列函数:
①f(x)=sinx; ②f(x)=π(x-1)2+3; ③![]() ④
④![]() ,
,
其中是一阶格点函数的有 .;
 23.已知函数f(x)的图象是两条直线的一部分,其定义域为
23.已知函数f(x)的图象是两条直线的一部分,其定义域为
[-1,0]∪(0,1),则不等式f(x)-f(-x)>-1的解集是 .
24.已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() 满足
满足
![]() ,且
,且![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 为奇函数;③
为奇函数;③![]() 是周期函数;④
是周期函数;④![]() 在
在![]() 内为单调函数其中正确的结论是
(填上所有正确结论的序号)
内为单调函数其中正确的结论是
(填上所有正确结论的序号)
25.定义运算x※y=![]() ,若m-1※m=m-1,则m的取值范围是
,若m-1※m=m-1,则m的取值范围是
26.已知![]() ,记
,记![]() ,(其中
,(其中![]() ),例如:
),例如:![]()
![]() 。设
。设![]() ,且满足
,且满足![]() ,和
,和![]() 则有序数组
则有序数组![]() 是 ________
是 ________
27.定义:若存在常数![]() ,使得对定义域
,使得对定义域![]() 内的任意两个
内的任意两个![]() ,均有
,均有![]() 成立,则称函数
成立,则称函数![]() 在定义域
在定义域![]() 上满足利普希茨条件。若函数
上满足利普希茨条件。若函数![]() 满足利普希茨条件,则常数
满足利普希茨条件,则常数![]() 的最小值为_________。
的最小值为_________。
1. 2. . 3. D 4. C 5. C 6. B 7. B 8. 9. (D)
10. A 11. C 12. D 13. B
14. B 15. 16. B 17. D 18. A 19. B 20. B 21. D 22. D
23. A 24. A 25. B 26. A 27. B 28. A 29. A 30. D 31. B 32. A 33. D 34. D 35. B 36. D 37. C 38. B 39. A 40.A 41. A 42. B 43.
1.![]() 2. 2 . 3. 30 4. 5 5.
2. 2 . 3. 30 4. 5 5. ![]() 6.
6.![]() 7.
7. ![]() 8.
8. ![]() 9.
9. ![]() 10.
10. ![]() 12. (4)
12. (4)
13. [ABE或BDEF(选一种即可)] 14. ![]()
![]() 15.
15. ![]() 16. (6:2:3;)
17.
16. (6:2:3;)
17. ![]()
18. ②③④⑤ 19. ![]() 20.
20. ![]() 21. 13 22. ①②④ 23. -1≤x<-
21. 13 22. ①②④ 23. -1≤x<-![]() 或0<x≤1
或0<x≤1
24. ②③ 25. ![]() 26.
26. ![]() 。
。  27.
27. ![]()