高考数学二轮复习函数三要素的综合考查
一.函数三要素(定义域、值域、对应关系)的求法:(学生做题归纳)
二.高考题热身
1.(06湖北卷)设![]() ,则
,则![]() 的定义域为_______________
的定义域为_______________
解:f(x)的定义域是(-2,2),故应有-2<![]() <2且-2<
<2且-2<![]() <2解得-4<x<-1或1<x<4故选B
<2解得-4<x<-1或1<x<4故选B
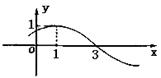
2.(06湖南卷)函数![]() 的定义域是_______ [4, +∞)
的定义域是_______ [4, +∞)
3.(07陕西卷)函数f(x)= (x∈R)的值域是( )
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
4.(06浙江卷)对a,b![]() R,记max{a,b}=
R,记max{a,b}=![]() ,函数f(x)=max{x+1,x-2}(x
,函数f(x)=max{x+1,x-2}(x![]() R)的最小值是____.
R)的最小值是____.
解:当x<-1时,x+1=-x-1,x-2=2-x,因为(-x-1)-(2-x)=-3<0,所以2-x>-x-1;当-1£x<0.5时,x+1=x+1,x-2=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当0.5£x<2时,x+1³2-x;当x³2时,x+1=x+1,x-2=x-2,显然x+1>x-2;
故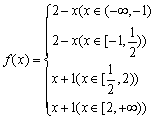 据此求得最小值为
据此求得最小值为![]() 。选C
。选C
5.(07安徽卷)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______。
_______。
解:由![]() 得
得![]() ,所以
,所以![]() ,则
,则![]() 。
。
6. (07山东卷)设f(x)= 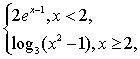 则不等式f(x)>2的解集为_____(1,2)
则不等式f(x)>2的解集为_____(1,2)![]() (
(![]() ,+∞)
,+∞)
解:令![]() >2(x<2),解得1<x<2。令
>2(x<2),解得1<x<2。令![]() >2(x³2)解得xÎ(
>2(x³2)解得xÎ(![]() ,+∞)
,+∞)
7. (05江苏卷2)函数![]() 的反函数的解析表达式为_______________.
的反函数的解析表达式为_______________.![]()
8.已知f(cosx)=cos5x,则f(sinx)=___________.
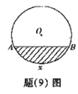 9.(06重庆卷)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是
9.(06重庆卷)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是
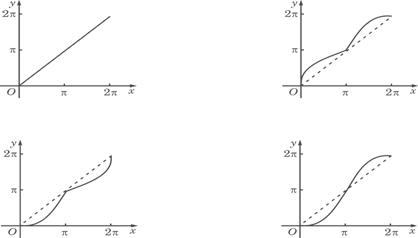
解析:如图所示,单位圆中![]() 的长为x,
的长为x,![]()
![]() 与弦AB所围成的弓形面积的2倍,当
与弦AB所围成的弓形面积的2倍,当![]() 的长小于半圆时,函数y=f(x)的值增加的越来越快,当
的长小于半圆时,函数y=f(x)的值增加的越来越快,当![]() 的长大于半圆时,函数y=f(x)的值增加的越来越慢,所以函数y=f(x)的图像是D.
的长大于半圆时,函数y=f(x)的值增加的越来越慢,所以函数y=f(x)的图像是D.
10. (05浙江理3)设f(x)=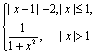 ,则f[f(
,则f[f(![]() )]= ________________
)]= ________________ ![]()
12. (04年北京文8) 函数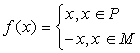 ,其中P、M为实数集R的两个非空子集,又规定
,其中P、M为实数集R的两个非空子集,又规定![]() ,
,![]() ,给出下列四个判断:
,给出下列四个判断:
①若![]() ,则
,则![]() ②若
②若![]() ,则
,则![]()
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]()
其中正确判断有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
三.典型例题
例1.(上海春) 设函数![]() .(1)在区间[-2,6]上画出函数
.(1)在区间[-2,6]上画出函数![]() 的图像;
的图像;
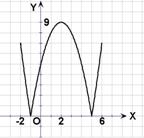 (2)设集合
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明; (3)当
之间的关系,并给出证明; (3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图像位于函数f(x)图像的上方.
的图像位于函数f(x)图像的上方.
解:(1)(要求列表描点) (2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,由于
,由于![]() 在
在![]() 和[2,5]上单调递减,在[-1,2]和
和[2,5]上单调递减,在[-1,2]和![]() 上单调递增,因此
上单调递增,因此
![]() .
.
由于![]() .
.
(3)[解法一] 当![]() 时,
时,![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() . 又
. 又![]() ,
,
① 当![]() ,即
,即![]() 时,取
时,取![]() ,
,
![]()
![]()
. ![]() , 则
, 则![]() .
.
② 当![]() ,即
,即![]() 时,取
时,取![]() ,
, ![]() =
=![]() .
.
由 ①、②可知,当![]() 时,
时,![]() ,
,![]() .
.
因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
[解法二] 当![]() 时,
时,![]() .由
.由![]()
得![]() , 令
, 令 ![]() ,
,
解得 ![]() 或
或![]() ,
,
在区间[-1,5]上,当![]() 时,
时,![]() 的图像与函数f(x)的图像只交于一点
的图像与函数f(x)的图像只交于一点![]() ; 当
; 当![]() 时,
时,![]() 的图像与函数f(x)的图像没有交点. 如图可知,由于直线
的图像与函数f(x)的图像没有交点. 如图可知,由于直线![]() 过点
过点![]() ,当
,当![]() 时,直线
时,直线![]() 是由直线
是由直线![]() 绕点
绕点![]() 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间![]() 上,
上,![]() 的图像位于函数f(x)图像的上方.
的图像位于函数f(x)图像的上方.
例2.(全国卷Ⅱ理17设函数![]() ,求使
,求使![]() 的
的![]() 取值范围.
取值范围.
解:由于![]() 是增函数,
是增函数,![]() 等价于
等价于![]() ①
①
⑴当![]() 时,
时,![]() ,∴①式恒成立。
,∴①式恒成立。
⑵当![]() 时,
时,![]() ,①式化为
,①式化为![]() ,即
,即![]() 。
。
⑶当![]() 时,
时,![]() ,①式无解。
综上,
,①式无解。
综上,![]() 的取值范围为
的取值范围为![]()
例3.已知函数![]() (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式; (2)设k>1,解关于x的不等式;![]()
【正确解答】(1)将![]()
得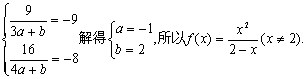
(2)不等式即为![]()
即![]()
①当![]()
②当![]()
③![]() .
.
例4.(全国II卷)设![]() ,函数
,函数![]() 若
若![]() 的解集为A,
的解集为A,![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
解:由f(x)为二次函数知![]() ,令f(x)=0解得其两根为
,令f(x)=0解得其两根为![]()
由此可知![]()
(i)当![]() 时,
时,![]()
![]() 的充要条件是
的充要条件是![]() ,即
,即![]() 解得
解得![]()
(ii)当![]() 时,
时,![]()
![]() 的充要条件是
的充要条件是![]() ,即
,即![]() 解得
解得![]()
综上,使![]() 成立的a的取值范围为
成立的a的取值范围为![]()
例5.(上海文22)(本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分,计18分)对定义域是![]() 、
、![]() 的函数y=f(x)、y=g(x),规定:函数
的函数y=f(x)、y=g(x),规定:函数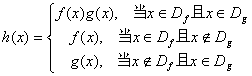 。
。
(1)若函数![]() ,
,![]() ,写出函数
,写出函数![]() 的解析式;(2)求问题(1)中函数
的解析式;(2)求问题(1)中函数![]() 的值域; (3)若
的值域; (3)若![]() ,其中
,其中![]() 是常数,且
是常数,且![]() ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数![]() ,及一个
,及一个![]() 的值,使得
的值,使得![]() ,并予以证明。
,并予以证明。
解(3)[解法一]令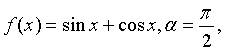 则
则![]()
于是![]()
[解法二]令![]() ,
,
则![]()
于是![]()
例6.设![]() 的值域为[-1,4],求a、b的值.
的值域为[-1,4],求a、b的值.
例7:已知函数f(x)=![]() ,x∈[1,+∞
,x∈[1,+∞![]() ,(1)当a=0.5时,求函数f(x)的最小值
,(1)当a=0.5时,求函数f(x)的最小值![]()
(2)若对任意x∈[1,+∞![]() ,f(x)>0恒成立,试求实数a的取值范围
,f(x)>0恒成立,试求实数a的取值范围![]()
(1)解![]() 当a=
当a=![]() 时,f(x)=x+
时,f(x)=x+![]() +2
+2
∵f(x)在区间[1,+∞![]() 上为增函数,∴f(x)在区间[1,+∞
上为增函数,∴f(x)在区间[1,+∞![]() 上的最小值为f(1)=
上的最小值为f(1)=![]()
![]()
(2)解法一![]() 在区间[1,+∞
在区间[1,+∞![]() 上,f(x)=
上,f(x)=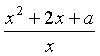 >0恒成立
>0恒成立![]() x2+2x+a>0恒成立
x2+2x+a>0恒成立![]()
设y=x2+2x+a,x∈[1,+∞![]() ,∵y=x2+2x+a=(x+1)2+a-1递增,
,∵y=x2+2x+a=(x+1)2+a-1递增,
∴当x=1时,ymin=3+a,当且仅当ymin=3+a>0时,函数f(x)>0恒成立,故a>-3![]()
解法二![]() f(x)=x+
f(x)=x+![]() +2,x∈[1,+∞
+2,x∈[1,+∞![]()
当a≥0时,函数f(x)的值恒为正; 当a<0时,函数f(x)递增,故当x=1时,f(x)min=3+a,
当且仅当f(x)min=3+a>0时,函数f(x)>0恒成立,故a>-3![]()
点评![]() 本题主要考查函数的最小值以及单调性问题,着重于学生的综合分析能力以及运算能力
本题主要考查函数的最小值以及单调性问题,着重于学生的综合分析能力以及运算能力![]() 解题的关健是把求a的取值范围的问题转化为函数的最值问题.通过求f(x)的最值问题来求a的取值范围,体现了转化的思想与分类讨论的思想
解题的关健是把求a的取值范围的问题转化为函数的最值问题.通过求f(x)的最值问题来求a的取值范围,体现了转化的思想与分类讨论的思想![]()
四.课后练习
1.已知f(xn)=lgx(n∈N*),则f(2)=_________________.
2.已知函数f(x)定义域为R+,且满足条件f(x)=f![]() ·lgx+1,f(x)=_______
·lgx+1,f(x)=_______
3.(04年湖北3)已知![]() 的解析式
的解析式
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(04年湖北7)函数![]() 上的最大值和最小值之和为a,则a的值为( )
上的最大值和最小值之和为a,则a的值为( )
A.0.25 B.0.5 C.2 D.4
5. (04天津12)定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
的值为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7. ![]()
8.方程cos2x+sinx=a有实数解,求实数a的取值范围.
9.已知函数f(x)满足f(logax)=![]() (其中a>0,a≠1,x>0),求f(x)的表达式
(其中a>0,a≠1,x>0),求f(x)的表达式![]()
解![]() (1)令t=logax(a>1,t>0;0<a<1,t<0),则x=at
(1)令t=logax(a>1,t>0;0<a<1,t<0),则x=at![]()
因此f(t)=![]() (at-a-t) ∴f(x)=
(at-a-t) ∴f(x)=![]() (ax-a-x)(a>1,x>0;0<a<1,x<0)
(ax-a-x)(a>1,x>0;0<a<1,x<0)
10(福建卷理19)已知函数![]() 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;(Ⅱ)求函数y=f(x)的单调区间.
解:(1)由函数f(x)的图象在点M(-1f(-1))处的 切线方程为x+2y+5=0,知
![]()
![]()
![]()
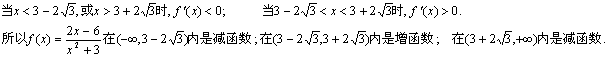
58.(重庆卷) 已知定义域为R的函数f(x)满足![]()
(I)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(II)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式
的解析表达式
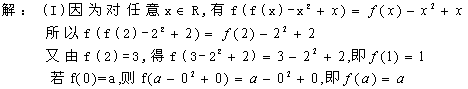
 55、(天津文15)设
55、(天津文15)设![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() 。
。