高考数学二轮复习圆锥曲线考点透析
【考点聚焦】
考点1:圆锥曲线的定义与标准方程的求法;
考点2:离心率与准线方程;
【考点小测】
1.(天津卷)如果双曲线的两个焦点分别为![]() 、
、![]() ,一条渐近线方程为
,一条渐近线方程为![]() ,那么它的两条准线间的距离是( )
,那么它的两条准线间的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:如果双曲线的两个焦点分别为![]() 、
、![]() ,一条渐近线方程为
,一条渐近线方程为![]() ,∴
,∴ 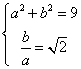 ,解得
,解得 ,所以它的两条准线间的距离是
,所以它的两条准线间的距离是![]() ,选C.
,选C.
2.(福建卷)已知双曲线![]() (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A.( 1,2) B. (1,2) C.[2,+∞] D.(2,+∞)
解析:双曲线![]() 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为![]() 的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率
的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率![]() ,∴
,∴ ![]() ≥
≥![]() ,离心率e2=
,离心率e2=![]() ,∴ e≥2,选C
,∴ e≥2,选C
3.(广东卷)已知双曲线![]() ,则双曲线右支上的点
,则双曲线右支上的点![]() 到右焦点的距离与点
到右焦点的距离与点![]() 到右准线的距离之比等于
到右准线的距离之比等于
A.![]() B.
B. ![]() C.
2
D. 4
C.
2
D. 4
解析:依题意可知 ![]() ,
,![]() ,故选C.
,故选C.
4.(辽宁卷)曲线![]() 与曲线
与曲线![]() 的
的
(A)焦距相等 (B) 离心率相等 (C)焦点相同 (D)准线相同
【解析】由![]() 知该方程表示焦点在x轴上的椭圆,由
知该方程表示焦点在x轴上的椭圆,由![]() 知该方程表示焦点在y轴上的双曲线,故只能选择答案A。
知该方程表示焦点在y轴上的双曲线,故只能选择答案A。
【点评】本题考查了椭圆和双曲线方程及各参数的几何意义,同时着重考查了审题能力即参数范围对该题的影响。
5.(全国卷I)双曲线![]() 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:双曲线![]() 的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为
的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为![]() ,∴ m=
,∴ m=![]() ,选A.
,选A.
6.(全国II)已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是
(A)2 (B)6 (C)4 (D)12
解析(数形结合)由椭圆的定义椭圆上一点到两焦点的距离之和等于长轴长2a,可得![]() 的周长为4a=
的周长为4a=![]() ,所以选C
,所以选C
7.(山东卷)在给定椭圆中,过焦点且垂直于长轴的弦长为![]() ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
解:不妨设椭圆方程为![]() (a>b>0),则有
(a>b>0),则有![]() ,据此求出e=
,据此求出e=![]() ,选B
,选B
8.(四川卷)已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于
的轨迹所包围的图形的面积等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,设P点的坐标为(x,y),
,设P点的坐标为(x,y),
则![]() ,即
,即![]() ,所以点
,所以点![]() 的轨迹所包围的图形的面积等于4π,选B.
的轨迹所包围的图形的面积等于4π,选B.
9.(四川卷)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 两点向抛物线的准线作垂线,垂足分别为
两点向抛物线的准线作垂线,垂足分别为![]() ,则梯形
,则梯形![]() 的面积为
的面积为
(A)48 (B)56 (C)64 (D)72
解析:直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 两点向抛物线的准线作垂线,垂足分别为
两点向抛物线的准线作垂线,垂足分别为![]() ,联立方程组得
,联立方程组得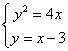 ,消元得
,消元得![]() ,解得
,解得![]() ,和
,和![]() ,∴ AP=10,BQ=2,PQ=8,梯形
,∴ AP=10,BQ=2,PQ=8,梯形![]() 的面积为48,选A.
的面积为48,选A.
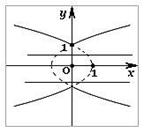 10.(上海卷)若曲线
10.(上海卷)若曲线![]() =
=![]() +1与直线
+1与直线![]() =
=![]() +
+![]() 没有公共点,
没有公共点,
则![]() 、
、![]() 分别应满足的条件是 .
分别应满足的条件是 .
解:作出函数![]() 的图象,
的图象,
如右图所示:
所以,![]() ;
;
【典型考例】
【问题1】求圆锥曲线的标准方程、离心率、准线方程等
例1.设椭圆的中心在原点,坐标轴为对称轴, 一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上较近的端点距离为![]() -4,求此椭圆方程、离心率、准线方程及准线间的距离.
-4,求此椭圆方程、离心率、准线方程及准线间的距离.
解:设椭圆的方程为![]() 或
或![]() ,则
,则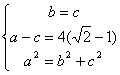 ,解之得:
,解之得:![]() ,b=c=4.则所求的椭圆的方程为
,b=c=4.则所求的椭圆的方程为![]() 或
或![]() ,离心率
,离心率![]() ;准线方程
;准线方程![]() ,两准线的距离为16.
,两准线的距离为16.
例2.(北京卷)椭圆![]() 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,,
P F1=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,,
P F1=![]() ,, P F2=
,, P F2=![]() .(I)求椭圆C的方程;(II)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
.(I)求椭圆C的方程;(II)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
解法一:(Ⅰ)因为点P在椭圆C上,所以![]() ,a=3.
,a=3.
在Rt△PF1F2中,![]() 故椭圆的半焦距c=
故椭圆的半焦距c=![]() ,
,
从而b2=a2-c2=4,
所以椭圆C的方程为![]() =1.
=1.
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2). 由圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1). 从而可设直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得 (4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称. 所以![]() 解得
解得![]() ,
,
所以直线l的方程为![]() 即8x-9y+25=0. (经检验,符合题意)
即8x-9y+25=0. (经检验,符合题意)
解法二:(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1![]() x2且
x2且
![]() ①
①
![]() ②
②
由①-②得
![]() ③
③
因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2,
代入③得![]() =
=![]() ,即直线l的斜率为
,即直线l的斜率为![]() ,
,
所以直线l的方程为y-1=![]() (x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意.)
(x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意.)
 【问题2】圆锥曲线的定义的问题
【问题2】圆锥曲线的定义的问题
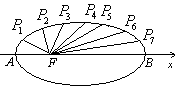
例3.(四川卷)如图,把椭圆![]() 的长轴
的长轴![]() 分成
分成![]() 等份,过每个分点作
等份,过每个分点作![]() 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于![]() 七个点,
七个点,![]() 是椭圆的一个焦点,则
是椭圆的一个焦点,则
![]() ;
;
例4.(江西卷)P是双曲线![]() 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则PM-PN的最大值为( )
A. 6 B.7 C.8 D.9
解:设双曲线的两个焦点分别是F1(-5,0)与F2(5,0),则这两点正好是两圆的圆心,当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大,此时PM-PN=(PF1-2)-(PF2-1)=10-1=9故选B
【问题3】直线与圆锥曲线位置关系问题
利用数形结合法或将它们的方程组成的方程组转化为一元二次方程,利用判别式、韦达定理来求解或证明.
例5.P104例3
例6.(浙江卷),椭圆![]() =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=![]() .(Ⅰ)求椭圆方程;(Ⅱ)设F
.(Ⅰ)求椭圆方程;(Ⅱ)设F![]() 、F
、F![]() 分别为椭圆的左、右焦点,M为线段AF
分别为椭圆的左、右焦点,M为线段AF![]() 的中点,求证:∠ATM=∠AF
的中点,求证:∠ATM=∠AF![]() T.
T.
本题主要考查直线与椭圆的位置关系、椭圆的几何性质,同时考察解析几何的基本思想方法和综合解题能力。
解:(I)过点![]() 、
、![]() 的直线方程为
的直线方程为![]()
因为由题意得 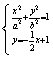 有惟一解,
有惟一解,
即![]() 有惟一解,
有惟一解,
所以![]() (
(![]() ),
),
故 ![]()
又因为 ![]() 即
即 ![]() 所以
所以
![]()
从而得 ![]() 故所求的椭圆方程为
故所求的椭圆方程为 ![]()
(II)由(I)得 ![]() 故
故![]() 从而
从而![]()
由 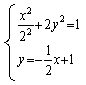 解得
解得![]() 所以
所以 ![]()
因为![]() 又
又![]()
![]() 得
得
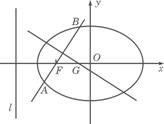
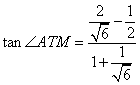
![]() 因此
因此![]()
例7.(福建卷)已知椭圆![]() 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(Ⅰ)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(Ⅱ)设过点F且不与坐标轴垂直交椭圆于A、B两点,线段
AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力。
 解:(I)
解:(I)![]()
![]() 圆过点O、F,
圆过点O、F,
![]() 圆心M在直线
圆心M在直线![]() 上。
上。
设![]() 则圆半径
则圆半径
![]()
由![]() 得
得![]() 解得
解得![]()
![]() 所求圆的方程为
所求圆的方程为![]()
(II)设直线AB的方程为![]()
代入![]() 整理得
整理得![]()
![]() 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,![]() 方程有两个不等实根。
方程有两个不等实根。
记![]() 中点
中点![]() 则
则![]()
![]() 的垂直平分线NG的方程为
的垂直平分线NG的方程为![]() 令
令![]() 得
得
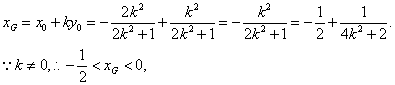
![]() 点G横坐标的取值范围为
点G横坐标的取值范围为![]()
例8.(湖北卷)设![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且![]() 为它的右准线。(Ⅰ)、求椭圆的方程;(Ⅱ)、设
为它的右准线。(Ⅰ)、求椭圆的方程;(Ⅱ)、设![]() 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 的点
的点![]() ,证明点
,证明点![]() 在以
在以![]() 为直径的圆内。
为直径的圆内。
 点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力。
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力。
解:(Ⅰ)依题意得 a=2c,![]() =4,解得a=2,c=1,从而b=
=4,解得a=2,c=1,从而b=![]() .
.
故椭圆的方程为 ![]() .
.
(Ⅱ)解法1:由(Ⅰ)得A(-2,0),B(2,0).设M(x0,y0).
∵M点在椭圆上,∴y0=![]() (4-x02).
1
(4-x02).
1
又点M异于顶点A、B,∴-2<x0<2,由P、A、M三点共线可以得P(4,![]() ).
).
从而![]() =(x0-2,y0),
=(x0-2,y0),![]() =(2,
=(2,![]() ).
).
∴![]() ·
·![]() =2x0-4+
=2x0-4+![]() =
=![]() (x02-4+3y02). 2
(x02-4+3y02). 2
将1代入2,化简得![]() ·
·![]() =
=![]() (2-x0).
(2-x0).
∵2-x0>0,∴![]() ·
·![]() >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内。
解法2:由(Ⅰ)得A(-2,0),B(2,0).设M(x1,y1),N(x2,y2),
则-2<x1<2,-2<x2<2,又MN的中点Q的坐标为(![]() ,
,![]() ),
),
依题意,计算点B到圆心Q的距离与半径的差
![]() -
-![]() =(
=(![]() -2)2+(
-2)2+(![]() )2-
)2-![]() [(x1-x2)2+(y1-y2)2]
[(x1-x2)2+(y1-y2)2]
=(x1-2) (x2-2)+y1y1 3
又直线AP的方程为y=![]() ,直线BP的方程为y=
,直线BP的方程为y=![]() ,
,
而点两直线AP与BP的交点P在准线x=4上,
∴![]() ,即y2=
,即y2=![]() 4
4
又点M在椭圆上,则![]() ,即
,即![]() 5
5
于是将4、5代入3,化简后可得![]() -
-![]() =
=![]() .
.
从而,点B在以MN为直径的圆内。
例9.(上海卷)已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
 (2)若
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)过原点![]() 的直线交椭圆于点
的直线交椭圆于点![]() ,求
,求![]() 面积的最大值。
面积的最大值。
解(1)由已知得椭圆的半长轴a=2,半焦距c=![]() ,则半短轴b=1.
,则半短轴b=1.
又椭圆的焦点在x轴上, ∴椭圆的标准方程为![]()
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
| 由 |
| 得 |
|
| y= | y0=2y- |
由,点P在椭圆上,得![]() ,
,
∴线段PA中点M的轨迹方程是![]() .
.
(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入![]() ,
,
解得B(![]() ,
,![]() ),C(-
),C(-![]() ,-
,-![]() ),
),
则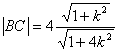 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=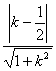 ,
,
∴△ABC的面积S△ABC=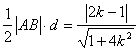
于是S△ABC=![]()
由![]() ≥-1,得S△ABC≤
≥-1,得S△ABC≤![]() ,其中,当k=-
,其中,当k=-![]() 时,等号成立.
时,等号成立.
∴S△ABC的最大值是![]() .
.
例10.(天津卷)如图,以椭圆![]() 的中心
的中心![]() 为圆心,分别以
为圆心,分别以![]() 和
和![]() 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点![]() 作垂直于
作垂直于![]() 轴的直线交大圆于第一象限内的点
轴的直线交大圆于第一象限内的点![]() .连结
.连结![]() 交小圆于点
交小圆于点![]() .设直线
.设直线![]() 是小圆的切线.
是小圆的切线.
(1)证明![]() ,并求直线
,并求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(2)设直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,证明
两点,证明![]() .
.
本小题主要考查椭圆的标准方程的几何性质、直线方程。平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.满分14分.
证明:(Ⅰ)由题设条件知,![]() ∽
∽![]() 故
故
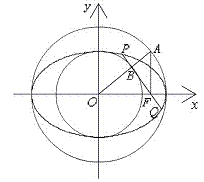
![]() ,即
,即![]()
因此,![]()
在![]() ,
, ![]()
因此,![]()
在![]() 中 ,
中 ,![]() .
.
于是,直线OA的斜率![]() .设直线BF的斜率为
.设直线BF的斜率为![]() ,则
,则![]() .
.
这时,直线BF与![]() 轴的交点为
轴的交点为![]()
(Ⅱ)由(Ⅰ),得直线BF得方程为![]() 且
且![]() ②
②
由已知,设![]() 、
、![]() ,则它们的坐标漫步方程组
,则它们的坐标漫步方程组
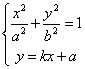 ③
③
由方程组③消去![]() ,并整理得
,并整理得 ![]()
由式①、②和④, 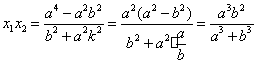
由方程组③消去![]() ,并整理得
,并整理得 ![]() ⑤
⑤
由式②和⑤, 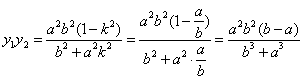
综上,得到![]()
注意到![]() ,得
,得
![]()
![]()
![]()
课后训练
1.(安徽卷)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:椭圆![]() 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线![]() 的焦点为(2,0),则
的焦点为(2,0),则![]() ,故选D。
,故选D。
2.(天津卷)椭圆的中心为点![]() ,它的一个焦点为
,它的一个焦点为![]() ,相应于焦点
,相应于焦点![]() 的准线方程为
的准线方程为![]() ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:椭圆的中心为点![]() 它的一个焦点为
它的一个焦点为![]() ∴
半焦距
∴
半焦距![]() ,相应于焦点F的准线方程为
,相应于焦点F的准线方程为![]() ∴
∴ ![]() ,
,![]() ,则这个椭圆的方程是
,则这个椭圆的方程是![]() ,选D.
,选D.
3. (山东卷)设直线![]() 关于原点对称的直线为
关于原点对称的直线为![]() ,若
,若![]() 与椭圆
与椭圆![]() 的交点为A、B、,点
的交点为A、B、,点![]() 为椭圆上的动点,则使
为椭圆上的动点,则使![]() 的面积为0.5的点
的面积为0.5的点![]() 的个数为( B )
的个数为( B )
(A)1 (B)2 (C)3 (D)4
4. (江苏卷)点P(-3,1)在椭圆![]() 的左准线上.过点P且方向为a=(2,-5)的光线,经直线
的左准线上.过点P且方向为a=(2,-5)的光线,经直线![]() =-2反射后通过椭圆的左焦点,则这个椭圆的离心率为(A )
=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为(A )
( A ) ![]() (
B )
(
B ) ![]() (
C )
(
C ) ![]() ( D )
( D )
![]()
5. (重庆卷)已知![]() ,B是圆F:
,B是圆F:![]() (F为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
(F为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为![]() 。
。
6.(江苏卷)已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0).
(6,0).
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程。
的双曲线的标准方程。
本小题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力。
解:(1)由题意可设所求椭圆的标准方程为![]() (a>b>0),其半焦距c=6
(a>b>0),其半焦距c=6
![]() ∴
∴![]() ,b2=a2-c2=9.
,b2=a2-c2=9.
所以所求椭圆的标准方程为![]()
(2)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为点P,(2,5)、F1,(0,-6)、F2,(0,6).
设所求双曲线的标准方程为![]() 由题意知,半焦距c1=6
由题意知,半焦距c1=6
![]()
![]() ,b12=c12-a12=36-20=16. 所以所求双曲线的标准方程为
,b12=c12-a12=36-20=16. 所以所求双曲线的标准方程为![]()
7.(全国卷I)在平面直角坐标系![]() 中,有一个以
中,有一个以![]() 和
和![]() 为焦点、离心率为
为焦点、离心率为![]() 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与![]() 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量![]() 。求:
。求:
(Ⅰ)点M的轨迹方程; (Ⅱ)![]() 的最小值。
的最小值。
.解: 椭圆方程可写为: + =1 式中a>b>0 , 且 得a2=4,b2=1,所以曲线C的方程为: x2+ =1 (x>0,y>0). y=2(0<x<1) y '=-
设P(x0,y0),因P在C上,有0<x0<1, y0=2, y 'x=x0= - ,得切线AB的方程为:
y=- (x-x0)+y0 . 设A(x,0)和B(0,y),由切线方程得 x= , y= .
由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为:
+ =1 (x>1,y>2)
(Ⅱ) ![]() 2= x2+y2, y2= =4+ ,
2= x2+y2, y2= =4+ ,
∴![]() 2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
故![]() 的最小值为3.
的最小值为3.
8.(上海卷)在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.(15班)
[解](1)设过点T(3,0)的直线![]() 交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线![]() 的钭率不存在时,直线
的钭率不存在时,直线![]() 的方程为x=3,此时,直线
的方程为x=3,此时,直线![]() 与抛物线相交于点A(3,
与抛物线相交于点A(3,![]() )、B(3,-
)、B(3,-![]() ).
∴
).
∴![]() =3;
=3;
当直线![]() 的钭率存在时,设直线
的钭率存在时,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]() ,
,
由![]() 得
得 ![]()
又 ∵ ![]() ,
,
∴![]() ,
,
综上所述,命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线![]() 交抛物线y2=2x于A、B两点,如果
交抛物线y2=2x于A、B两点,如果![]() =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(![]() ,1),此时
,1),此时![]() =3,直线AB的方程为:
=3,直线AB的方程为:![]() ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2)
满足![]() =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).
9.(全国II)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明·为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.(15班)
解:(Ⅰ)由已知条件,得F(0,1),λ>0.设A(x1,y1),B(x2,y2).由=λ,
即得 (-x1,1-y)=λ(x2,y2-1),
将①式两边平方并把y1=x12,y2=x22代入得 y1=λ2y2 ③
解②、③式得y1=λ,y2=,且有x1x2=-λx22=-4λy2=-4,
抛物线方程为y=x2,求导得y′=x.
所以过抛物线上A、B两点的切线方程分别是
y=x1(x-x1)+y1,y=x2(x-x2)+y2,即y=x1x-x12,y=x2x-x22.
解出两条切线的交点M的坐标为(,)=(,-1). ……4分
所以·=(,-2)·(x2-x1,y2-y1)=(x22-x12)-2(x22-x12)=0
所以·为定值,其值为0. ……7分
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=ABFM.
FM===
==+.
因为AF、BF分别等于A、B到抛物线准线y=-1的距离,所以
AB=AF+BF=y1+y2+2=λ++2=(+)2.
于是 S=ABFM=(+)3,
由+≥2知S≥4,且当λ=1时,S取得最小值4.
10.(山东卷)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.。(Ⅰ)求椭圆的方程;
(Ⅱ)直线![]() 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.(15班)
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.(15班)
解:设椭圆方程为![]()
(Ⅰ)由已知得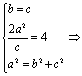
![]() ∴所求椭圆方程为
∴所求椭圆方程为 ![]() .
.
(Ⅱ)解法一:由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
由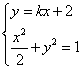 ,消去y得关于x的方程:
,消去y得关于x的方程:![]()
由直线![]() 与椭圆相交于A、B两点,
与椭圆相交于A、B两点,![]() 解得
解得![]()
又由韦达定理得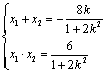
![]()
![]()
原点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
解法1:对![]() 两边平方整理得:
两边平方整理得:![]() (*)
(*)
∵![]() ,
,
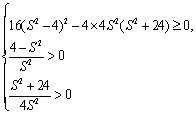 整理得:
整理得:![]()
又![]() ,
, ![]() 从而
从而![]() 的最大值为
的最大值为![]() ,
,
此时代入方程(*)得 ![]()
![]()
所以,所求直线方程为:![]() .
.
解法2:令![]() , 则
, 则![]()
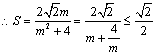
当且仅当![]() 即
即![]() 时,
时, ![]() 此时
此时![]() .
.
所以,所求直线方程为![]()
解法二:由题意知直线l的斜率存在且不为零.设直线l的方程为![]() ,则直线l与x轴的交点
,则直线l与x轴的交点![]() ,
,
由解法一知![]() 且
且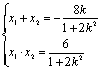 ,
,
解法1:![]() =
=![]()
![]()
![]()
![]() .
.
下同解法一.
解法2:![]()
![]()
![]() =
=![]()
下同解法一.