高考数学二轮复习导数与单调性的综合考查
一、小题（共10题）
1、函数
是减函数的区间为( )
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
2. 在函数
的图象上，其切线的倾斜角小于
的点中，坐标为整数的点的个数（ ）
A．3 B．2 C．1 D．0
3． 对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有（ ）
A.f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
4.设
，曲线
在点
处切处的倾斜角的取值范围为
，则P到曲线对称轴距离的取值范围（ ）
A．
B．
C． 
D． 
5．与直线
的平行的抛物线
的切线方程是 （ ）
A．
B．
C．
D．
6．设
分别是定义在R上的奇函数和偶函数，
，当
时，
且
则不等式
的解集是 （ ）
A．
B．
C．
D．
7．函数f(x)=x(x－1)(x－2)·…·(x－100)在
处的导数值为
（
）
A.0 B.
C.200
.100！
8．过点（－1，0）作抛物线
的切线，则其中一条切线为 （ ）
（A）
（B）
（C）
（D）
小题答案：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | D | B | B | D | D | D | D |
9．设函数
，（
、
、
是两两不等的常数），则
．0
10.解析：曲线
和在它们的交点坐标是(1，1)，两条切线方程分别是y=－x+2和y=2x－1，它们与
轴所围成的三角形的面积是
.
二．解答题
1.已知抛物线C1：y=x2+2x和C：y=－x2+a，如果直线l同时是C1和C2的切线，称l是C1和C2的公切线，公切线上两个切点之间的线段，称为公切线段.
（Ⅰ）a取什么值时，C1和C2有且仅有一条公切线？写出此公切线的方程；
（Ⅱ）若C1和C2有两条公切线，证明相应的两条公切线段互相平分.
解：本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力，满分12分
（Ⅰ）解：函数y=x2+2x的导数y′=2x+2,曲线C1在点P（x1,x
+2x1）的切线方程是：
y－(x+2x1)=(2x1+2)(x－x1),即
y=(2x1+2)x－x ①
函数y=－x2+a的导数y′=－2x, 曲线C2
在点Q（x2,－x
+a）的切线方程是
即y－(－x+a)=－2x2(x－x2). y=－2x2x+x+a .
②
如果直线l是过P和Q的公切线，则①式和②式都是l的方程，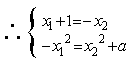
消去x2得方程 2x+2x2+1+a=0.
若判别式△=4－4×2（1+a）=0时，即a=－
时解得x1=－，此时点P与Q重合.
即当a=－时C1和C2有且仅有一条公切线，由①得公切线方程为 y=x－
.
（Ⅱ）证明：由（Ⅰ）可知.当a<－时C1和C2有两条公切线
设一条公切线上切点为：P（x1,y1）, Q（x2 , y2 ）.
其中P在C1上，Q在C2上，则有x1+x2=－1,
y1+y2=x+2x1+(－x+a)= x+2x1－(x1+1)2+a=－1+a .
线段PQ的中点为
同理，另一条公切线段P′Q′的中点也是
所以公切线段PQ和P′Q′互相平分.
2．已知f(x)=x2+ax+b, g(x)=x2+cx+d,又f(2x+1)=4g(x),且
，f(5)=30,则求g(4)。
解：
∵f(2x+1)=4g(x) ∴
∴
又 f(5)=30=25+10+b ∴b=-5 d=
∴g(x)=x2+2x
∴g(4)=
3．已知向量
=（1，0），
=（0，1），函数
的图象在
轴上的截距为1，在=2处切线的方向向量为
，并且函数当
时取得极值。
（1）求
的解析式；（2）求的单调递增区间；（3）求的极值。
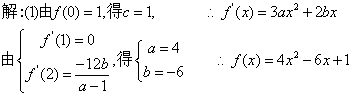
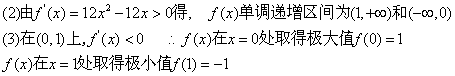
4.(全国卷Ⅱ)设a为实数,函数
(Ⅰ)求的极值.
(Ⅱ)当a在什么范围内取值时,曲线
轴仅有一个交点.
解：(I)
=3
－2－1 若=0，则==－
，=1
当变化时，，变化情况如下表：
|
| (－∞，－ | － | (－ | 1 | (1，+∞) |
|
| + | 0 | － | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
∴的极大值是
，极小值是
(II)函数
，由此可知，取足够大的正数时，有>0，取足够小的负数时有<0，所以曲线=与轴至少有一个交点结合的单调性可知：
当的极大值
<0，即
时，它的极小值也小于0，因此曲线=与轴仅有一个交点，它在(1，+∞)上。
当的极小值－1>0即
(1，+∞)时，它的极大值也大于0，因此曲线=与轴仅有一个交点，它在(－∞，－)上。∴当∪(1，+∞)时，曲线=与轴仅有一个交点。
6．（湖南卷）设
，点P（
，0）是函数
的图象的一个公共点，两函数的图象在点P处有相同的切线.；（Ⅰ）用表示a，b，c；
（Ⅱ）若函数
在（－1，3）上单调递减，求的取值范围.
解：（I）因为函数，
的图象都过点（，0），所以
，
即
.因为
所以
. 
又因为，在点（，0）处有相同的切线，所以
而
将代入上式得
因此
故，
，
（II）解法一
.
当
时，函数单调递减.
由
，若
；若
由题意，函数在（－1，3）上单调递减，则
所以
又当
时，函数在（－1，3）上单调递减.
所以的取值范围为
解法二：
因为函数在（－1，3）上单调递减，且
是（－1，3）
上的抛物线，
所以
即
解得
所以的取值范围为
7.（安徽卷）设函数
，已知
是奇函数。
（Ⅰ）求、的值。（Ⅱ）求的单调区间与极值。
解析：（Ⅰ）∵
，∴
。
从而
＝
是一个奇函数，所以
得
，由奇函数定义得
；
（Ⅱ）由（Ⅰ）知
，从而
，由此可知，
和
是函数是单调递增区间；
是函数是单调递减区间；
在
时，取得极大值，极大值为
，在
时，取得极小值，极小值为
。
8．（北京卷）已知函数
在点
处取得极大值
，其导函数
的图象经过点
，
，如图所示.求：（Ⅰ）的值； （Ⅱ）
的值.
解析：解法一： （Ⅰ）由图象可知，在（－∞，1）上
,在(1,2)上
,在上, 故在
,上递增,在(1,2)上递减,因此在
处取得极大值,所以
.
(Ⅱ)
由
得
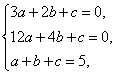解得
解法二:(Ⅰ)同解法一.
(Ⅱ)设
又
所以
由
,即
得
, 所以
.
9．（湖南卷）已知函数
. （Ｉ）讨论函数
的单调性； （Ⅱ）若曲线
上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，求实数a的取值范围.
解 （Ⅰ）由题设知
.令
.
当（i）a>0时，
若
，则
，所以在区间
上是增函数；
若
，则
，所以在区间
上是减函数；
若
，则，所以在区间
上是增函数；
（i i）当a＜0时，
若
，则，所以在区间上是减函数；
若，则，所以在区间上是减函数；
若
，则，所以在区间
上是增函数；
若
，则，所以在区间
上是减函数.
（Ⅱ）由（Ⅰ）的讨论及题设知，曲线上的两点A、B的纵坐标为函数的极值，且函数在
处分别是取得极值
，
.
因为线段AB与x轴有公共点，所以
.即
.所以
. 故
.
解得 －1≤a＜0或3≤a≤4.即所求实数a的取值范围是[-1，0)∪[3，4].
10．（全国卷I）设为实数，函数
在
和
都是增函数，求的取值范围。
解:f'(x)=3x2－2ax+(a2－1),其判别式△=4a2－12a2+12=12－8a2.
(ⅰ)若△=0,即a=±,当x∈(－∞,),或x∈(,+∞)时,
f'(x)>0,f(x)在(－∞,+∞)为增函数.所以a=±.
(ⅱ)若△=12－8a2<0,恒有f'(x)>0,f(x)在(－∞,+∞)为增函数,
所以a2>,即a∈(－∞,－)∪(,+∞)
(ⅲ)若△12－8a2>0,即－<a<,令f'(x)=0,解得x1=,x2=.
当x∈(－∞,x1),或x∈(x2,+∞)时,f'(x)>0,f(x)为增函数;当x∈(x1,x2)时,f'(x)<0,f(x)为减函数.依题意x1≥0且x2≤1.由x1≥0得a≥,解得1≤a<
由x2≤1得≤3－a,解得－<a<,从而a∈[1,)
综上,a的取值范围为(－∞,－]∪[,+∞)∪[1,),即a∈(－∞,－]∪[1,∞).
11．（全国II）设函数f(x)＝(x＋1)ln(x＋1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．
解法一：令g(x)＝(x＋1)ln(x＋1)－ax，
对函数g(x)求导数：g′(x)＝ln(x＋1)＋1－a 令g′(x)＝0，解得x＝ea－1－1， ……5分
(i)当a≤1时，对所有x＞0，g′(x)＞0，所以g(x)在[0，＋∞)上是增函数，
又g(0)＝0，所以对x≥0，都有g(x)≥g(0)，
即当a≤1时，对于所有x≥0，都有 f(x)≥ax．……9分
(ii)当a＞1时，对于0＜x＜ea－1－1，g′(x)＜0，所以g(x)在(0，ea－1－1)是减函数，
又g(0)＝0，所以对0＜x＜ea－1－1，都有g(x)＜g(0)，即当a＞1时，对所有的x≥0，都有f(x)≥ax成立．
综上，a的取值范围是（－∞，1]． ……12分
解法二：令g(x)＝(x＋1)ln(x＋1)－ax，于是不等式f(x)≥ax成立
即为g(x)≥g(0)成立． ……3分
对函数g(x)求导数：g′(x)＝ln(x＋1)＋1－a令g′(x)＝0，解得x＝ea－1－1， ……6分
当x＞ ea－1－1时，g′(x)＞0，g(x)为增函数，
当－1＜x＜ea－1－1，g′(x)＜0，g(x)为减函数， ……9分
所以要对所有x≥0都有g(x)≥g(0)充要条件为ea－1－1≤0．由此得a≤1，即a的取值范围是（－∞，1]．