三角函数总结及统练
一. 教学内容:
三角函数总结及统练
(一)基础知识
1. 与角![]() 终边相同的角的集合
终边相同的角的集合![]()
2. 三角函数的定义(六种)——三角函数是![]() 、
、![]() 、
、![]() 三个量的比值
三个量的比值
3. 三角函数的符号——口诀:一正二弦,三切四余弦。
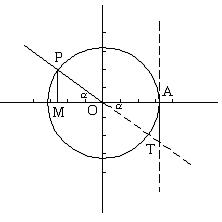
4. 三角函数线
正弦线MP=![]()
余弦线OM=![]()
正切线AT=![]()
5. 同角三角函数的关系
平方关系: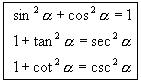 商数关系:
商数关系: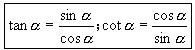
倒数关系:![]()
![]()
![]()
口诀:凑一拆一;切割化弦;化异为同。
6. 诱导公式——口诀:奇变偶不变,符号看象限。
|
|
|
|
|
|
|
|
|
| 正弦 |
|
|
|
|
|
|
|
| 余弦 |
|
|
|
|
|
|
|
| 正切 |
|
|
|
|
|
|
|
| 余切 |
|
|
|
|
|
|
|
7. 两角和与差的三角函数
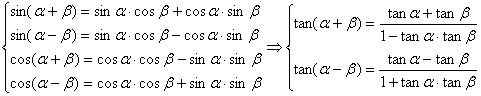
8. 二倍角公式——代换:令![]()
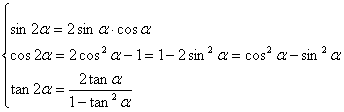
降幂公式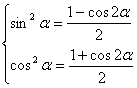
半角公式:![]() ;
;![]() ;
;![]()
![]()
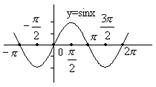
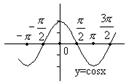
9. 三角函数的图象和性质
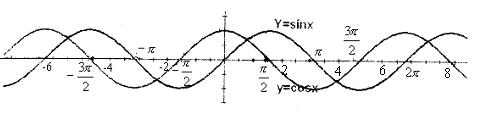
| 函数 |
|
|
|
| 图象 |
|
|
|
| 定义域 | R | R |
|
| 值域 最值 |
|
| R 无最大值 无最小值 |
| 周期性 | 周期为 | 周期为 | 周期为 |
| 奇偶性 | 奇函数 | 偶函数 | 奇函数 |
| 单调性 | 在 上都是增函数;在 上都是减函数( | 在 | 在 |
10. 函数![]() 的图象变换
的图象变换 ![]()
函数![]() 的图象可以通过下列两种方式得到:
的图象可以通过下列两种方式得到:
(1)![]()
![]()
![]()
(2)![]()
![]()
![]()
(二)数学思想与基本解题方法
1. 式子变形原则:凑一拆一;切割化弦;化异为同。
2. 诱导公式原则:奇变偶不变,符号看象限。
3. 估用公式原则:一看角度,二看名称,三看特点。
4. 角的和与差的相对性
如:![]() -
-![]()
角的倍角与半角的相对性
如:![]()
5. 升幂与降幂:升幂角减半,降幂角加倍。
6. 数形结合:心中有图,观图解题。
7. 等价转化的思想:将未知转化为已知,将复杂转化为简单,将高级转化为低级。
8. 换元的手段:通过换元实现转化的目的。
【典型例题】
1. 如:![]() (化成一个角的一个三角函数)
(化成一个角的一个三角函数)
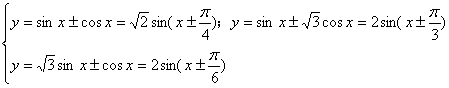
[例1] 求下列函数的最大值和最小值及何时取到?
(1)![]()
(2)![]()
解:
(1)![]() ,
,![]() ,
,![]()
![]()
(2)![]() ,
,![]() ,
,![]()
![]() ,
,![]()
2.“1”的妙用——凑一拆一
熟悉下列三角式子的化简
![]()
![]()
![]() ;
;![]()
[例2] 化简![]() 。
。
答案:![]()
3. 化异为同
[例3] 已知![]() ,求:
,求:
(1)![]() (2)
(2)![]()
答案:(1)3;(2)![]()
[例4] 已知![]() ,求:
,求: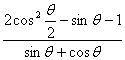
答案:![]()
4. ![]() 与
与![]() 间的相互转化
间的相互转化
(1)若![]() ,则
,则![]() ;
;![]() ;
;![]() =
=
![]()
(2)若![]() ,则
,则![]() ;
;![]()
(3)![]()
[例5] 化简:![]() 。
。
答案:![]()
[例6] 若![]() 在第二象限,
在第二象限,![]() ,求
,求![]() 。
。
答案:![]()
5. 互为余角的三角函数相互转化
若![]() ,则
,则![]() ;
;![]()
[例7] 已知![]() ,则
,则![]() 。
。
答案:![]()
[例8] 求值:![]() 。
。
答案:![]()
[例9] 求值:![]() 。
。
答案:![]()
6. 公式的变形及活用
(1)![]()
(2)若![]()
[例10] 计算![]() 。
。
答案:![]()
[例11] ![]() 。
。
答案:![]()
7. 角的和与差的相对性;角的倍角与半角的相对性
[例12] 若![]() ,则
,则![]() 。
。
答案:7
[例13] 若![]() ,则
,则![]() 。
。
答案:![]()
[例14] 在![]() 中,A为最小角,C为最大角,且
中,A为最小角,C为最大角,且![]() ,
,![]() ,求
,求![]() 的值。
的值。
答案:![]()
8. 角的范围的限定
由于条件中的三角式是有范围限制的,所以求值时可排除值的多样性。
[例15] 已知![]() ,求
,求![]() 。
。
答案:![]()
[例16] 若![]() 是第二象限角且
是第二象限角且![]() ,求
,求![]() 的值。
的值。
解法一:利用公式![]() 然后限定角的范围。
然后限定角的范围。
解法二:设![]() 利用平方和求
利用平方和求![]() 的值,然后限定角的范围。
的值,然后限定角的范围。
解法三:利用![]()
![]() ,可回避限定角的范围。
,可回避限定角的范围。
答案:![]()
9. 在三角形中的有关问题
![]() ;
;![]() ;
;![]()
结论:![]() ;
;![]()
![]() ;
;![]()
[例17] 已知A、B、C是![]() 的内角且
的内角且![]() ,试判断此三角形的形状。
,试判断此三角形的形状。
答案:等腰三角形,B=C
[例18] 在锐角三角形ABC中,求证:![]()
证明:由![]() 则
则![]()
故![]() 同理
同理![]()
![]()
三式相加,得证。
10. 形如![]() 的化简
的化简
[例19] 求值:(1)![]() (2)
(2)![]()
答案:(1)![]() (2)
(2)![]()
11. 三角函数图像和性质的应用
会求——定义域、值域、最值、周期、对称轴、单调区间(“一套”);会解——简单的三角不等式、三角方程、比较大小。
[例20] 求下列函数的定义域。
(1)![]()
(2)![]()
答案:
(1)![]()
(2)![]()
[例21] 求下列函数的值域。
(1)![]()
(2)若![]() 是锐角,则
是锐角,则![]() 的值域。
的值域。
答案:(1)![]() (2)
(2)![]()
12. 可化为形如:![]() 的形式(一个角的一个三角函数)
的形式(一个角的一个三角函数)
[例22] 已知函数![]() ,求“一套”。
,求“一套”。
答案:![]() ,定义域:R;值域:
,定义域:R;值域:![]() ,
,![]() ,
,![]() ;
;![]()
对称轴![]() 增区间:
增区间:![]()
减区间:![]()
13. 函数![]() 的图像的变换——两个题型,两种途径
的图像的变换——两个题型,两种途径
题型一:已知解析式![]() 确定其变换方法
确定其变换方法
变换有两种途径:其一,先平移后横向伸缩;其二,先横向伸缩后平移。
注:关注先横向伸缩后平移时平移的单位与![]() 的关系
的关系
题型二:由函数图像求其解析式![]()
[例23] 已知函数![]() ,(
,(![]() ,
,![]() )在一个周期内,当
)在一个周期内,当![]() 时,
时,![]() 有最大值为2,当
有最大值为2,当![]() 时,
时,![]() 有最小值为
有最小值为![]() ,求函数表达式,并画出函数
,求函数表达式,并画出函数![]() 在一个周期内的简图。(用五点法列表描点)
在一个周期内的简图。(用五点法列表描点)
答案:![]()
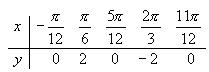
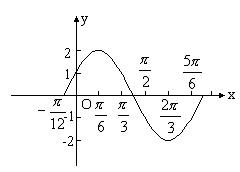
14. 可化为形如:![]() ,
,![]() (定义域有限制的一元二次函数)
(定义域有限制的一元二次函数)
[例24] 求函数![]() 的值域
的值域
解:![]()
[例25] 已知![]() ,若记其最大值为
,若记其最大值为![]() ,求
,求![]() 的解析式。
的解析式。
解:![]() ,当
,当![]() 时,
时,![]()
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
15. 周期函数与周期
[例26] 已知函数![]() 对定义域中每一个
对定义域中每一个![]() 都有
都有![]() ,其中
,其中![]() ,则
,则![]() 的周期
。
的周期
。
解:T
[例27] 已知奇函数![]() 对定义域中每一个
对定义域中每一个![]() 都有
都有![]() 成立,求其周期。
成立,求其周期。
解:4
[例28] 已知奇函数![]() 对定义域中每一个
对定义域中每一个![]() 都有
都有![]() 成立,求其周期。
成立,求其周期。
解:8
[例29] 已知奇函数![]() 对定义域中每一个
对定义域中每一个![]() 都有
都有![]() 成立,求其周期。
成立,求其周期。
解:6
[例30] 已知奇函数![]() 对定义域中每一个
对定义域中每一个![]() 都有
都有![]() 成立 ,求其周期。
成立 ,求其周期。
解:6
16. 函数与方程的思想
[例31] 方程![]() 的解的个数 。
的解的个数 。
解:63
【模拟试题】(答题时间:60分钟)
1. 求下列函数的最大值和最小值及何时取到?
![]()
2. 已知![]() ,求:
,求:![]()
3. 设![]() ,则
,则![]() 。
。
4. 求![]() 的最大值和最小值。
的最大值和最小值。
5. 求值:![]() 。
。
6. 若![]() ;
;![]() ,求
,求![]()
7. 已知![]() 、
、![]() 且
且![]() ,
,![]() ,求
,求![]() 的值。
的值。
8. ![]() 为何值时方程
为何值时方程![]() 有解?
有解?
9. 方程![]() ,
,![]() 有两解时求
有两解时求![]() 的值。
的值。
10. 求值:
(1)![]()
(2)![]()
11. 求下列函数的定义域。
![]()
12. 已知函数![]() ,当
,当![]() 时,求函数的最大值和最小值及何时取到?
时,求函数的最大值和最小值及何时取到?
【试题答案】
1.
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
2.
![]() 3.
3. ![]()
4. 令![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
5. ![]() 6.
6. ![]()
7.
提示:关键是角的范围的限定,逐层限定角的范围,逐步求细。
解:![]()
![]()
又由![]() 得
得![]() ,
,![]() 得
得![]()
则![]() 故
故![]()
8. ![]()
9. ![]()
10.(1)![]() (2)
(2)![]()
11.
![]() (
(![]() )
)
12.
当![]() 时,
时,![]() ;
;![]() 时,
时,![]()