高考数学复习三角测试题
1.(北师大版第59页A组第2题)正弦定理与余弦定理
在![]()
![]() 中,若
中,若 ![]() ,则
,则![]() .
.
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
变式1:在![]()
![]() 中,若
中,若 ![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________.
答案:1或3
变式2:在![]()
![]() 中,若
中,若 ![]() ,
,![]() ,
,![]() ,则此三角形的周长为__________.
,则此三角形的周长为__________.
答案:![]()
变式3:已知a、b、c是△ABC中∠A、∠B、∠C的对边,S是△ABC的面积.若a=4,b=5,S=5![]() ,求c的长度.
,求c的长度.
解:∵S=![]() absinC,∴sinC=
absinC,∴sinC=![]() ,于是∠C=60°或∠C=120°
,于是∠C=60°或∠C=120°
又∵c2=a2+b2-2abcosC,
当∠C=60°时,c2=a2+b2-ab,c=![]()
当∠C=120°时,c2=a2+b2+ab,c=![]()
∴c的长度为![]() 或
或![]()
2.(北师大版第63页A组第6题)三角形中的几何计算
在![]()
![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线交过点
的平分线交过点![]() 且与
且与![]() 平行的线于点
平行的线于点![]() .求
.求![]()
![]() 的面积.
的面积.
变式1:已知![]() 的周长为
的周长为![]() ,且
,且![]() .
.
(I)求边![]() 的长;
的长;
(II)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数.
的度数.
解:(I)由题意及正弦定理,得![]() ,
,
![]() ,
,
两式相减,得![]() .
.
(II)由![]() 的面积
的面积![]() ,得
,得![]() ,
,
由余弦定理,得![]()
![]() ,
,
所以![]() .
.
变式2:△ABC中,![]() 则△ABC的周长为( ).
则△ABC的周长为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解:在![]() 中,由正弦定理得:
中,由正弦定理得: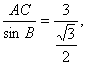 化简得:AC=
化简得:AC=![]()
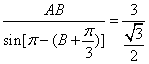 ,化简得:AB=
,化简得:AB=![]() ,
,
所以三角形△ABC的周长为:3+AC+AB=3+![]() +
+![]()
=3+![]()
故选D
变式3:在![]() ,求(1)
,求(1)![]() (2)若点
(2)若点![]()
解:(1)由![]() 得:
得:![]()
![]() ,
,
由正弦定理知: 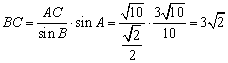 ,
,
(2)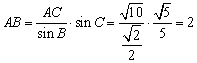 ,
,![]()
由余弦定理知:
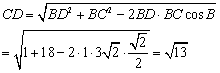
3.(北师大版第69页练习2第2题)解三角形的实际应用
某观察站B在城A的南偏西![]() 的方向,由A出发的一条公路走向是南偏东
的方向,由A出发的一条公路走向是南偏东![]() ,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?
,在B处测得公路上距B31km的C处有一人正沿公路向A城走去,走了20km之后到达D处,此时B,D间的距离为21km。这个人要走多少路才能到达A城?
变式1:如图,当甲船位于A处时获悉,在其正东方向
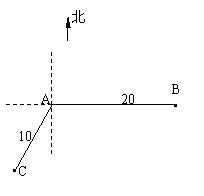 相距20海里的B处有一艘渔船遇险等待营救.甲船
相距20海里的B处有一艘渔船遇险等待营救.甲船
立即前往救援,同时把消息告知在甲船的南偏西30![]() ,
,
相距10海里C处的乙船,试问乙船应朝北偏东多少
度的方向沿直线前往B处救援(角度精确到1![]() )?
)?
解析:连接BC,由余弦定理得:
BC2=202+102-2×20×10COS120°=700.
即BC=10![]()
∵![]() ,
,
∴sin∠ACB=![]() ,
,
∵∠ACB<90°,∴![]() .
.
∴乙船应朝北偏东71°方向沿直线前往B处救援.
变式2:如图,测量河对岸的塔高![]() 时,可以选与塔底
时,可以选与塔底![]() 在同一水平面内的两个测点
在同一水平面内的两个测点![]() 与
与![]() .现测得
.现测得![]() ,并在点
,并在点![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,求塔高
,求塔高![]() .
.
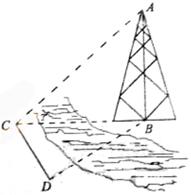
解:在![]() 中,
中,![]() .
.
由正弦定理得:![]() .
.
所以![]() .
.
在![]() 中,
中,![]() .
.
变式3: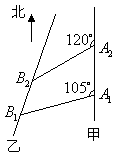 如图,甲船以每小时
如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
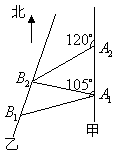 解法一:如图,连结
解法一:如图,连结![]() ,由已知
,由已知![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
由已知,![]() ,
,
![]() ,
,
在![]() 中,由余弦定理,得:
中,由余弦定理,得:
![]()
![]()
![]() .
.
![]() .
.
因此,乙船的速度的大小为![]() (海里/小时).
(海里/小时).
答:乙船每小时航行![]() 海里.
海里.
解法二:如图,连结![]() ,由已知
,由已知![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
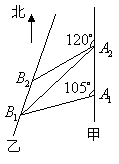
![]() ,
,
![]()
![]()
![]() .
.
在![]() 中,由余弦定理,
中,由余弦定理,
![]()
![]()
![]() .
.
![]() .
.
由正弦定理,得:
![]() ,
,
![]() ,即
,即![]() ,
,
![]() .
.
在![]() 中,由已知
中,由已知![]() ,由余弦定理,得:
,由余弦定理,得:
![]()
![]()
![]() .
.
![]() ,
,
乙船的速度的大小为![]() 海里/小时.
海里/小时.
答:乙船每小时航行![]() 海里.
海里.
4.(北师大版第60页A组第4题)三角函数图像变换
将函数![]() 的图像作怎样的变换可以得到函数
的图像作怎样的变换可以得到函数![]() 的图像?
的图像?
变式1:将函数![]() 的图像作怎样的变换可以得到函数
的图像作怎样的变换可以得到函数![]() 的图像?
的图像?
解:(1)先将函数![]() 图象上各点的纵坐标扩大为原来的2倍(横坐标不变),即可得到函数
图象上各点的纵坐标扩大为原来的2倍(横坐标不变),即可得到函数![]() 的图象;
的图象;
(2)再将函数![]() 上各点的横坐标缩小为原来的
上各点的横坐标缩小为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象;
的图象;
(3)再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.
变式2:将函数![]() 的图像作怎样的变换可以得到函数
的图像作怎样的变换可以得到函数![]() 的图像?
的图像?
解:(1)先将函数![]() 图象上各点的纵坐标缩小为原来的
图象上各点的纵坐标缩小为原来的![]() (横坐标不变),即可得到函数
(横坐标不变),即可得到函数![]() 的图象;
的图象;
(2)再将函数![]() 上各点的横坐标扩大为原来的2倍(纵坐标不变),得到函数
上各点的横坐标扩大为原来的2倍(纵坐标不变),得到函数![]() 的图象;
的图象;
(3)再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.
变式3:将函数![]() 的图像作怎样的变换可以得到函数
的图像作怎样的变换可以得到函数![]() 的图像?
的图像?
解:![]()
![]()
![]()
![]()
另解:
(1)先将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象;
的图象;
(2)再将函数![]() 上各点的横坐标扩大为原来的2倍(纵坐标不变),得到函数
上各点的横坐标扩大为原来的2倍(纵坐标不变),得到函数![]() 的图象;
的图象;
(3)再将函数![]() 图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到函数
图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到函数![]() 的图象.
的图象.
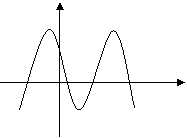
5.(北师大版第60页B组第1题)三角函数图像
函数![]() 一个周期的图像如图所示,试确定A,
一个周期的图像如图所示,试确定A,![]() 的值.
的值.
变式1:已知简谐运动![]() 的图象经过点
的图象经过点![]() ,则该简谐运动的最小正周期
,则该简谐运动的最小正周期![]() 和初相
和初相![]() 分别为( )
分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
答案选A
变式2:函数![]() 在区间
在区间![]() 的简图是( )
的简图是( )
答案选A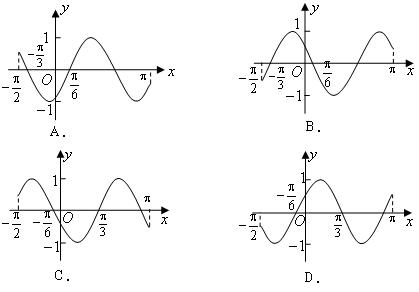
|
![]()
|
|
|
求![]() 和
和![]() 的值.
的值.
解:将![]() ,
,![]() 代入函数
代入函数![]() 得:
得:
![]() ,
,
因为![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
因此![]() .
.
6.(北师大版第60页A组第6题)三角函数性质
求下列函数的最大、最小值以及达到最大(小)值时![]() 的值的集合.
的值的集合.
(1) ![]() ;
(2)
;
(2) ![]()
变式1:已知函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,则
,则![]() 的最小值等于 ( )
的最小值等于 ( )
(A)![]() (B)
(B)![]() (C)2 (D)3
(C)2 (D)3
答案选B
变式2:函数y=2sinx的单调增区间是( )
A.[2kπ-![]() ,2kπ+
,2kπ+![]() ](k∈Z)
](k∈Z)
B.[2kπ+![]() ,2kπ+
,2kπ+![]() ](k∈Z)
](k∈Z)
C.[2kπ-π,2kπ](k∈Z)
D.[2kπ,2kπ+π](k∈Z)
答案选A.因为函数y=2x为增函数,因此求函数y=2sinx的单调增区间即求函数y=sinx的单调增区间.
变式3:关于x的函数f(x)=sin(x+![]() )有以下命题:
)有以下命题:
①对任意的![]() ,f(x)都是非奇非偶函数;
,f(x)都是非奇非偶函数;
②不存在![]() ,使f(x)既是奇函数,又是偶函数;
,使f(x)既是奇函数,又是偶函数;
③存在![]() ,使f(x)是奇函数;
,使f(x)是奇函数;
④对任意的![]() ,f(x)都不是偶函数。
,f(x)都不是偶函数。
其中一个假命题的序号是_____.因为当![]() =_____时,该命题的结论不成立。
=_____时,该命题的结论不成立。
答案:①,kπ(k∈Z);或者①,![]() +kπ(k∈Z);或者④,
+kπ(k∈Z);或者④,![]() +kπ(k∈Z)
+kπ(k∈Z)
解析:当![]() =2kπ,k∈Z时,f(x)=sinx是奇函数.当
=2kπ,k∈Z时,f(x)=sinx是奇函数.当![]() =2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数.当
=2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数.当![]() =2kπ+
=2kπ+![]() ,k∈Z时,f(x)=cosx,或当
,k∈Z时,f(x)=cosx,或当![]() =2kπ-
=2kπ-![]() ,k∈Z时,f(x)=-cosx,f(x)都是偶函数.所以②和③都是正确的.无论
,k∈Z时,f(x)=-cosx,f(x)都是偶函数.所以②和③都是正确的.无论![]() 为何值都不能使f(x)恒等于零.所以f(x)不能既是奇函数又是偶函数.①和④都是假命题.
为何值都不能使f(x)恒等于零.所以f(x)不能既是奇函数又是偶函数.①和④都是假命题.
7.(北师大版第66页B组第2题)同角三角函数的基本关系
已知![]() ,求
,求![]() .
.
变式1:已知![]() ,求
,求![]() 的值.
的值.
解:∵ ![]() ,
,
∴ ![]()
即 ![]()
∴ 当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
变式2:已知![]() ,那么角
,那么角![]() 是( ).
是( ).
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
答案选C.
变式3:![]() 是第四象限角,
是第四象限角,![]() ,则
,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案选D.
8.(北师大版第132页A组第4题)两角和与差及二倍角的三角函数
已知![]() ,
,![]() ,求
,求![]() ,
,![]() 的值.
的值.
变式1:在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值.
的值.
(Ⅰ)解:在![]() 中,
中,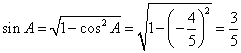 ,
,
由正弦定理, ![]() .
.
所以![]() .
.
(Ⅱ)解:因为![]() ,所以角
,所以角![]() 为钝角,从而角
为钝角,从而角![]() 为锐角,
为锐角,
于是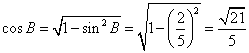 ,
,
![]() ,
,
![]() .
.
∴ ![]()
![]()
![]() .
.
变式2:在![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() 最大边的边长为
最大边的边长为![]() ,求最小边的边长.
,求最小边的边长.
解:(Ⅰ)![]() ,
,
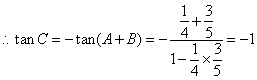 .
.
又![]() ,
,![]() .
.
(Ⅱ)![]() ,
,
![]() 边最大,即
边最大,即![]() .
.
又![]() ,
,
![]() 角
角![]() 最小,
最小,![]() 边为最小边.
边为最小边.
由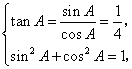 且
且![]() ,
,
得![]() .由
.由![]() 得:
得:![]() .
.
所以最小边![]() .
.
变式3:已知![]() ,且
,且![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() .
.
解:(Ⅰ)由![]() ,得
,得![]()
∴![]() ,于是
,于是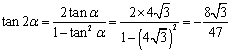
(Ⅱ)由![]() ,得
,得![]()
又∵![]() ,∴
,∴![]()
由![]() 得:
得:
![]()
![]()
所以![]() .
.
9.(北师大版第144页A组第1题)三角函数的简单应用
电流I随时间t
变化的关系式![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() .
.
(1) 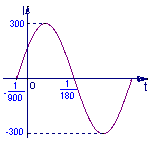 求电流I变化的周期;
求电流I变化的周期;
(2)
当![]() (单位
(单位![]() )时,求电流I.
)时,求电流I.
变式1:已知电流I与时间t的关系式为![]() .
.
(1)右图是![]() (ω>0,
(ω>0,![]() )
)
在一个周期内的图象,根据图中数据求![]() 的解析式;
的解析式;
(2)如果t在任意一段![]() 秒的时间内,电流
秒的时间内,电流![]() 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
解:(1)由图可知 A=300.
设t1=-![]() ,t2=
,t2=![]() ,
,
则周期T=2(t2-t1)=2(![]() +
+![]() )=
)=![]() .
.
∴ ω=![]() =150π.
=150π.
又当t=![]() 时,I=0,即sin(150π·
时,I=0,即sin(150π·![]() +
+![]() )=0,
)=0,
而![]() , ∴
, ∴ ![]() =
=![]() .
.
故所求的解析式为![]() .
.
(2)依题意,周期T≤![]() ,即
,即![]() ≤
≤![]() ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
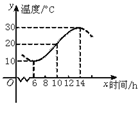 变式2:如图,某地一天从6时至14时的温度变化曲线近似
变式2:如图,某地一天从6时至14时的温度变化曲线近似
满足函数y=Asin(ωx+![]() )+b.
)+b.
(Ⅰ)求这段时间的最大温差;
(Ⅱ)写出这段曲线的函数解析式.
解:(1)由题中图所示,这段时间的最大温差是:
30-10=20(℃).
(2)图中从6时到14时的图象是函数y=Asin(ωx+![]() )+b的半个周期的图象,
)+b的半个周期的图象,
∴![]() ·
·![]() =14-6,解得ω=
=14-6,解得ω=![]() .
.
由图示,A=![]() (30-10)=10,b=
(30-10)=10,b=![]() (30+10)=20.
(30+10)=20.
这时y=10sin(![]() x+
x+![]() )+20.
)+20.
将x=6,y=10代入上式,可取![]() =
=![]() .
.
综上,所求的解析式为y=10sin(![]() x+
x+![]() )+20,x∈[6,14]
)+20,x∈[6,14]
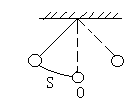 变式3:如图,单摆从某点给一个作用力后开始来回摆动,
变式3:如图,单摆从某点给一个作用力后开始来回摆动,
离开平衡位置O的距离s厘米和时间t秒的函数关系
为![]() .
.
(1)单摆摆动5秒时,离开平衡位置多少厘米?
(2)单摆摆动时,从最右边到最左边的距离为多少厘米?
(3)单摆来回摆动10次所需的时间为多少秒?
10.(北师大版第150页B组第6题)三角恒等变换
化简: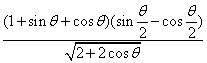 .
.
变式1:函数y=![]() 的最大值是( ).
的最大值是( ).
A.![]() -1 B.
-1 B.
![]() +1 C.1-
+1 C.1-![]() D.-1-
D.-1-![]()
答案选B
变式2:已知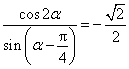 ,求
,求![]() 的值.
的值.
解:∵
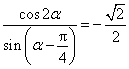 ,
,
∴ 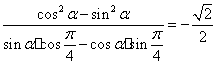
即
![]() .
.
变式3:已知函数![]() ,
,![]() .求
.求![]() 的最大值和最小值.
的最大值和最小值.
解: ![]()
![]() .
.
又![]() ,
,![]() ,即
,即![]() ,
,
![]() .
.